distribuce
jádrem problémů s deltou Dirac a podobnými matematickými objekty
je problém diferencovatelnosti. Jako Dirac je uvedeno v citaci výše, nemáte opravdu spustit do potíží, pokud používáte jeho funkce δ jako symbolické pravidlo pro to, jak to působí na ostatní funkce; nicméně, on pokračuje k odlišení δ v jeho výpočtů, a to je místo, kde problémy opravdu začít., Jak lze a priori vědět, „když jsou tyto operace přípustné“, když člověk nemá ani pevnou definici objektů, nebo co by to znamenalo jejich rozlišení? Uvidíme, jak tyto otázky vedou k odvození nových a přísně definovaných matematických objektů.
funkcionály
zvažte, jak obvykle určuje derivát (nebo antiderivativní) funkce. Za normálních okolností, s“ klasickými “ funkcemi, máte dobře definované pravidlo, které popisuje, jak funkce mapuje jednu sadu reálných čísel na jinou sadu, řekněme f: → → ℝ., Vzhledem k tomuto a definicím integrálu nebo derivátu lze pak jasně prozkoumat hodnoty, které tyto operátory přinášejí při aplikaci na funkci. V případě δ nemáme žádnou funkční definici, která by pokračovala v těchto liniích. Místo toho je v praxi δ nejvýrazněji definováno tím, jak funguje na jiných, dobře definovaných funkcích (jako v (3)). To je klíčový vhled, který vede k moderní teorii distribucí. Ukazuje se, že správným způsobem, jak matematicky zacházet s δ a velkou třídou podobných objektů, je přestat se je snažit definovat jako funkce vůbec., Tato linie myšlení je dobře popsán Jean Dieudonna ve své recenzi (viz ):
… jeden začíná s rodinou velmi „normální“ funkce (obvykle s
respektovat rozdílné vlastnosti), které splňují určité (obvykle
integral) vztahů, nebo na které některé operace jsou možné; a
pak jeden zjistí, že a priori větší rodiny funkcí splňuje
stejné vztahy, nebo mohou být podrobeny podobné operace. Mnoho otázek
pak může být přirozeně položeno: je tato nová rodina opravdu
odlišná od první?, Pokud ano, jaké jsou vztahy mezi
dvěma rodinami a lze dát přesný popis nového?
To je jen v poslední fázi „pravěku“, že to, co může být
nazvat revoluční hlediska se objeví, s myšlenkou, že
„nová rodina“ se může skládat z objektů jiných než funkce.
ostatní objekty zmiňované jsou funkcionály. Funkční
můžete považovat za funkci funkcí., Jako funkce je unikátní mapování z jedné sady
čísel do druhé, funkční F lze definovat jako mapování F: C →ℝ,
Kde C je nějaká sada funkcí. To znamená, že funkční mapy fungují na reálných číslech
., Jednoduchý příklad funkčního tohoto typu je určitý integrál:

který zřetelně přebírá funkci f z nějaké sady vhodně integrovatelné funkce a mapy, aby to reálné číslo, hodnota integrální, nebo plocha pod křivkou f(x) mezi body a a b. To je jen jeden příklad., Lze si představit nekonečný počet funkcionálů, a množiny funkcionálů, dalo by se i nadále zobecnit a definovat mapování z množiny funkcionálů na reálná čísla. To není ani tady, ani tam. Důležité je, že funkční koncept lze použít k definování distribucí.
sada testovacích funkcí
pro dosažení našeho cíle požadujeme ještě jednu definici. To znamená zadání sady C funkcí, ze kterých budou distribuce mapovat funkce na reálná čísla., Funkce jsou často shromažďovány v sadách, které specifikují jejich stupeň kontinuity, diferencovatelnosti a kontinuitu jejich derivátů. Říkáme, že funkce f je v sadě C⁰ (zápis f ∈ C⁰), pokud je kontinuální přes celou reálnou osu v tom smyslu, že limit na všech místech je stejný, pokud jsou užívány z vlevo nebo vpravo; není nutně diferencovatelná. Říkáme, že f ∈ C1, pokud jeho derivát existuje a je spojitý, tj. Například funkce g(x) = / x / je spojitá, ale není diferencovatelná při x= 0; g je v C⁰, ale ne v C1., Můžeme zobecnit a říci, že Cⁿ je sada funkcí, které mají pro spojité funkce, jejich první deriváty n, kde n je celé číslo.
jak se n zvětšuje, sady se stávají v jistém smyslu „menšími“; vždy můžete najít funkce(nekonečně mnoho!), které jsou v Cⁿ, ale ne Cⁿ ⁺ 1. Tyto „kontinuitní prostory“ proto tvoří posloupnost vnořených podmnožin, jak je znázorněno níže.

v dolní části tuto nekonečnou posloupnost množin funkcí najdeme sadu
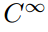
což je samozřejmě množina všech funkcí, které mají nekonečně mnoho kontinuální deriváty. V této druhé třídě je mnoho známých a přátelských funkcí(např. sin(x); cos (x); eˣ; všechny polynomy)., Tyto funkce se nazývají “ hladké „nebo“ dobře vychované“, protože na nich lze provádět diferenciaci tolik času, kolik se jim líbí bez péče. Ale zatímco tato sada má jistě nekonečně mnoho členů, jsou vzácné v tom smyslu, že většina funkcí není tak dobře vychovaná.
sada, která je vhodná pro definici distribucí, je ještě menší
než tato. Vyžaduje další kritérium: že funkce mají kompaktní podporu. Tento technický termín znamená jednoduše, že funkce má nenulové hodnoty v konečné doméně, a je rovnoměrně nulová mimo toto., Proto jsme se použít zápis
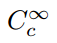
pro množinu nekonečně spojitě diferencovatelných funkcí s kompaktním podporu, a volání takové funkce testovací funkce. Abychom definovali třídu funkcionálů pomocí této sady jako domény, měli bychom si být jisti, že ve skutečnosti existují členové této sady., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

definice
od tohoto okamžiku je definice distribuce přímočará. Rozdělení je lineární funkční
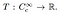
To je, to je mapování z množiny testovacích funkcí na reálné číslo. Analogicky k tomu, jak konkrétní funkce působí na vstupní číslo a vytváří výstup, jsou specifické distribuce definovány tím, jak transformují testovací funkce na čísla., Distribuční působení zkušební funkce φ lze zapsat jako T (φ), nebo běžně jako〈T, φ φ.
Nyní lze vidět, proč se distribuce nazývají zobecněné funkce. Pro jakékoliv
klasické funkce, pro něž integrál

je dobře definována, existuje odpovídající distribuční F takové, že 〈F,φ〉dává hodnotu tohoto integrálu., Existují však také distribuce, které neodpovídají klasickým funkcím; distribuce jsou obecnější. Jak by mělo být jasné, kanonickým příkladem distribuce, která neodpovídá klasické funkci, je Dirac δ., Proto jsme se konečně dorazí na plně přísné definice δ jako rozdělení takové, že

obecné nebo „Slabý“ Derivace
δ distribuce je pouze jeden z nekonečně mnoha distribucí, které nemají
odpovídá klasické funkce. Některé z nich můžeme získat rozlišováním δ ve smyslu rozdělení., Jak však koncept distribuce
řeší problém diferenciace, jak bylo diskutováno dříve? Potřebujeme pouze zobecnit koncept diferenciace, aby se vztahoval na distribuce.
zvažte funkci f ∈ C1, takže je nepřetržitě diferencovatelná. Výpočet pomocí integrace po částech, vidíme, že

Výraz v závorce zmizí, protože φ, jako testovací funkci, má kompaktní podporu., To zobecňuje na distribuci, že F‘, odpovídající funkce f‘:

Tento výpočet zobecňuje poměrně snadno distribucí, které neodpovídají klasické funkce f., Tímto způsobem můžeme definovat derivát T‘ T ve smyslu distribucí:

To je také někdy označovány jako slabé derivace, protože to rozšiřuje deriváty k funkcím, které by za normálních okolností neměl být diferencovatelné. To zobecňuje ještě více, na deriváty vyššího řádu., Můžeme definovat n-té derivace distribuční T jako T⁽ⁿ⁾, kde ta je rozdělení takové, že

Zde
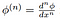
je klasická derivace funkce test, což je zajištěna
existuje podle definice testovací funkce!, Z toho vyplývá, že všechny distribuce jsou nekonečně diferencovatelné (ve smyslu distribucí).
tím se zcela odstraní Boj, kterému Dirac a další čelili při diferenciaci funkce δ. Podle toho, co jsme zde definovali, derivát δ jednoduše prosívá hodnotu jiné derivace funkcí na nulu., Formálně,

To poskytuje přísný matematický rámec pro deriváty δ, které se objevily v literatuře dlouho předtím, než tato teorie vznikla.
existuje řada dalších operací, které se vztahují na funkce, které byly zobecněny, aby se vztahovaly na distribuce. Mohou být přidány a odečteny, konvolvovány a transformovány pomocí Laplaceových a Fourierových transformací., Není však možné definovat násobení distribucí způsobem, který zachovává algebru, která se vztahuje na klasické funkce (Schwartzova věta o nemožnosti).