Icosahedron (Čeština)

pravidelný icosahedron je jednou z pěti platonických pevných látek. Jedná se o konvexní pravidelný mnohostěn složený z dvaceti trojúhelníkových ploch, s pěti setkáními na každém z dvanácti vrcholů. Má 30 okrajů a 12 vrcholů. Jeho dvojí polyhedron je dodecahedron.,

Rozměry

Pokud je délka hrany pravidelný dvacetistěn je , poloměr opsané koule (ten, který se dotýká icosahedron na všechny vrcholy), je

a poloměr vepsané koule (dotýkající se každého z icosahedron tváře) je

zatímco midradius, která se dotýká středu každé hrany, je

kde 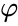(také volal ) je zlatý poměr.,

Oblast a objem

povrch a objem pravidelný dvacetistěn edge délka :

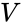
Kartézské souřadnice

následující Kartézské souřadnice, které definují vrcholy dvacetistěn s hranou délky 2, střed v počátku:

kde je zlatý poměr (také psáno τ)., Všimněte si, že tyto vrcholy tvoří pět sad tří vzájemně centrovaných, vzájemně ortogonálních zlatých obdélníků.

12 okrajů pravidelného oktahedronu lze rozdělit do zlatého poměru tak, aby výsledné vrcholy definovaly pravidelný ikosahedron. To se provádí první uvedení vektory podél osmistěn hran taková, že každá plocha je ohraničena cyklu, pak stejně tak rozdělení každé hrany do zlatá střední cesta podél směru jeho vektoru., Pět octahedra definování dané icosahedron tvoří pravidelný polyedrické sloučeniny, jako dva icosahedra, které může být definováno tímto způsobem z daného osmistěnu.

Stavební systém equiangular linky

následující konstrukce icoshaedron vyhýbá nudné výpočty v poli číslo nutné ve více základních přístupů.

Existence icosahedronu představuje existenci šesti rovnoúhlých čar v ., Opravdu, protínající takový systém equiangular linky s Euklidovský oblasti se soustředil na jejich společný průsečík výnosy dvanáct vrcholů pravidelný dvacetistěn, jak může být snadno kontrolovat. Naopak, za předpokladu existence pravidelného ikosahedronu, čáry definované jeho šesti páry protilehlých vrcholů tvoří rovnoúhlý systém.

abychom vytvořili takový ekviangulární systém, začneme maticí

čtvercové velikosti ., (Mnemotechnická pomůcka: matrix kóduje úhly, akutní pro pozitivní vstup, tupý jinak, mezi pěti cyklicky po sobě jdoucí vrcholy přilehlé k první vrchol dvacetistěn střed v počátku.)

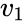
přímý výpočet poskytuje . To znamená, že má vlastní čísla , oba s multiplicity 3 od je symetrický a stopových 0., Matrix indukuje thusan Euklidovské konstrukce, na podíl prostoru , který je izomorfní od jádra má dimenzi 3. Obrázek pod projekce šest souřadných os vytváří tak vytvořilo systém šesti equiangular řádky v protínající po dvou na společné akutní úhel ., Ortogonální projekce do -eigenspace výnosy, tedy dvanáct vrcholů icosahedron.

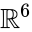
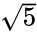
druhý jednoduchá konstrukce icosahedron používá zastoupení teorie střídavého skupiny působí přímým isometries na dvacetistěn.

Stellations

Podle konkrétních pravidel definovaných v knize padesát devět icosahedra, 59 stellations byly určeny pro pravidelný dvacetistěn. První formou je samotný icosahedron., Jedním z nich je pravidelná pevná látka Kepler-Poinsot. Tři jsou pravidelné složené polyhedry.

21 59 stellations

tváře icosahedron rozšířena směrem ven, jako roviny protínají, vymezování regionů v prostoru, jak dokládá tato stellation schéma křižovatky v jedné rovině.,

Geometric relations

Icosahedron as a snub tetrahedron.,

Icosahedron as an alternated truncated octahedron.

There are distortions of the icosahedron that, while no longer regular, are nevertheless vertex-uniform., Tyto jsou invariantní podle stejné rotace jako čtyřstěn, a jsou poněkud analogický s tupým krychle a tupým dvanáctistěn, včetně některých forem, které jsou chirální a některé s T-symetrie, tj. mají různé rovin symetrie z čtyřstěnu. Icosahedron má velké množství souhvězdí, včetně jednoho z Kepler-Poinsot polyhedra a některých pravidelných sloučenin, které by zde mohly být diskutovány.

icosahedron je mezi platonickými pevnými látkami jedinečný v tom, že má dihedrální úhel nejméně 120°. Jeho dihedrální úhel je přibližně 138,19°.,ss než 120° a nemohou být použity jako plochy konvexní pravidelný mnohostěn, protože taková konstrukce by splnění požadavku, aby nejméně tři tváře setkat na vrcholu a zanechat pozitivní vadu, pro skládání v třech rozměrech, icosahedra nemůže být použit jako buňky konvexní pravidelné polychoron, protože, podobně, nejméně tři buňky musí splňovat na hranu a zanechat pozitivní vadu, pro skládací ve čtyřech rozměrech (obecně pro konvexní polytope v rozměry nejméně tři aspekty musí splňovat na vrcholu a zanechat pozitivní vadu, pro skládací v n-prostoru)., Nicméně, při kombinaci s vhodným buňky s menší dihedrální úhly, icosahedra může být použit jako buňky v semi-pravidelné polychora (například urážka, 24-buňky), stejně jako šestiúhelníky může být použit jako obličeje v semi-pravidelný mnohostěn (například zkrácený dvacetistěn). Konečně, non-úhelník konvexní nenesou stejné přísné požadavky jako konvexní úhelník, a icosahedra jsou opravdu buněk dvacetistěnná 120-buněk, jedné z deseti non-konvexní pravidelné polychora.

icosahedron lze také nazvat gyroelongated pentagonální bipyramid., To může být rozložen do gyroelongated pětiboká pyramida a pětiúhelníkové pyramidy nebo do pětiúhelníkové antiprism a dvě stejné pětiúhelníkové pyramidy.

icosahedron může být také nazýván tupým čtyřstěnem, protože snubifikace pravidelného čtyřstěnu dává pravidelný ikosahedron., Alternativně, pomocí nomenklatury pro urážku mnohostěn, který odkazuje na krátkou krychle jako urážka cuboctahedron (cuboctahedron = opraveny kostka) a tupým dvanáctistěn jako urážka dvaatřicetistěn (dvaatřicetistěn = opraveny dvanáctistěn), jeden může volat icosahedron urážka, octahedron (osmistěn = opraveny čtyřstěn).

rektifikovaný icosahedron tvoří icosidodecahedron.

Icosahedron vs dvanáctistěn

Když dvacetistěn je vepsána do koule, to zabírá méně koule je objem (60.54%) než dvanáctistěn vepsaný ve stejné oblasti (66.49%).,

také, protože se jedná o duály, je možné transformovat jeden do druhého(viz níže).,

Icosahedron

Truncated icosahedron

Icosidodecahedron

Truncated dodecahedron

Dodecahedron

Uses and natural forms

In 1904, Ernst Haeckel described a number of species of Radiolaria, including Circogonia icosahedra, whose skeleton is shaped like a regular icosahedron. A copy of Haeckel’s illustration for this radiolarian appears in the article on regular polyhedra.

	V některých rpg her, dvacet oboustranný die (pro krátké, d20) se používá při určování úspěchu či neúspěchu akce. Tato die je ve formě pravidelného ikosahedronu. To může být očíslovány od „0“ do „9“ dvakrát (v jaké formě obvykle slouží jako deset kostkou, nebo d10), ale většina moderních verzích jsou označeny od „1“ do „20“. Viz systém d20.,

dvacetistěn je tří-dimenzionální herní deska pro Icosagame, dříve známý jako Ico Krystal Hry.

icosahedron se používá v deskové hře Scattergories vybrat písmeno abecedy. Šest málo používaných písmen, jako je X, Q A Z, jsou vynechány.

uvnitř Magic 8-Ball jsou na pravidelném icosahedronu vytištěny různé odpovědi na otázky ano-ne.

icosahedron zobrazený ve funkční podobě je vidět ve světlém odstínu Sol de la Flor., Růžice tvořená překrývajícími se kusy vykazuje podobnost s květinou Frangipani.

Pokud je každá hrana dvacetistěn je nahrazen jeden ohm rezistor, odpor mezi protilehlými vrcholy je 0,5 ohmu, a to mezi sousedními vrcholy 11/30 ohmů.

skupina symetrie icosahedronu je izomorfní ke střídavé skupině na pěti písmenech. Tato nonabelská jednoduchá skupina je jedinou netriviální normální podskupinou symetrické skupiny na pěti písmenech., Od Osnova skupiny z obecné rovnice pátého stupně je izomorfní k symetrické skupiny na pět písmen, a skutečnost, že dvacetistěnná skupiny je jednoduché a nonabelian znamená, že rovnice pátého stupně nemusí mít řešení v radikály. Důkaz o Abel-Ruffini teorém použití této jednoduché skutečnosti, a Felix Klein napsal knihu, která využila teorie dvacetistěnná symetrie odvodit analytické řešení obecné rovnice pátého stupně.,

Viz také

Šablona:Wiktionarypar

• Komolý dvacetistěn
• Pravidelný mnohostěn
• Geodetické sítě použít iterativně půlen icosahedron pro generování sítí v oblasti
• Jessen je icosahedron

Šablona:Wikisource1911Enc

Šablony:Commonscat

• Weisstein, Eric W., „Icosahedron“ z MathWorld.
• papírové modely icosahedronu
• jednotný Polyhedra
• k. J. M., MacLean, Geometrická Analýza Pěti Platonické Pevné látky a Jiné Semi-Pravidelný Mnohostěn
• Interaktivní Icosahedron model – funguje přímo ve vašem webovém prohlížeči
• Virtuální Reality Mnohostěn Encyklopedie Mnohostěn
• Tulane.,edu je diskuse o super konstrukci a icosahedron
• Papírové Modely Mnohostěnů Mnoho odkazů
• Origami Polyhedra – Models je vyroben s Modulární Origami
• video z dvacetistěnná zrcadlo je sochařství

Šablona:Mnohostěn

az:Ikosaedrca:Icosàedrecs:Dvacetistěnda:Ikosaederet:Ikosaeedereo:Dudekedrofa:بیستوجهیit:Icosaedrohe:איקוסהדרוןlv:Ikosaedrshu:Ikozaédernl:Icosaëderno:Ikosaederpl:Dwudziestościan foremnypt:Icosaedrosimple:Icosahedronsq:Ikosaedri jsem rregulltsr:Икосаедарsv:Ikosaederta:vypukla முக்கோணகம்th:ทรงยี่สิบหน้าuk:Ікосаедр.