LEONARDO FIBONACCI – ITALSKÝ MATEMATIK (NAPSAL LEBER POČÍTADLA)

Leonardo Pisa (Fibonacci), (c.1170-1250)

13. Století italský Leonardo z Pisy, lépe známý jeho přezdívkou Fibonacci, byl snad nejvíce talentovaný Západní matematik Středověku. O jeho životě je známo jen málo, kromě toho, že byl synem celního úředníka a jako dítě cestoval se svým otcem po severní Africe, kde se dozvěděl o arabské matematice., Po návratu do Itálie, pomohl šířit tyto znalosti po celé Evropě, a tak uvést do pohybu omlazení v Evropské matematice, která ležela do značné míry spící po staletí během temných věků.

zejména, v roce 1202, napsal velmi vlivnou knihu s názvem „Liber Abaci“ („Kniha Výpočet“), v níž byl povýšen použití Hind-arabské číslice systému, popisuje jeho mnoho výhod pro obchodníky a matematici podobně přes nešikovný systém Římských číslic, pak se v Evropě používají., I přes své zjevné výhody, zavádění systému v Evropě byl pomalý (to byl koneckonců v době křížové Výpravy proti Islámu, čas, ve kterém něco arabština byla vnímána s velkým podezřením), a arabské číslice byly dokonce zakázány ve městě Florencie v roce 1299, pod záminkou, že byli snadněji zfalšovat, než Římské číslice. Nakonec však zvítězil zdravý rozum a nový systém byl přijat po celé Evropě do 15.století, čímž byl římský systém zastaralý., V této práci byla také poprvé použita vodorovná lišta pro zlomky (i když podle arabské praxe umístění zlomku vlevo od celého čísla).

Fibonacciho Posloupnosti.

objev slavné Fibonacciho posloupnosti,

Fibonacci je nejlépe známý, i když pro jeho dovoz do Evropy konkrétní číslo sekvence, které se od té doby stala známou jako Fibonacciho Čísla, nebo Fibonacciho Posloupnosti., Objevil sekvence – první rekurzivní číselné řady, známé v Evropě – zatímco s ohledem na praktický problém v „Liber Abaci“, zahrnující růst hypotetické populace králíků na základě idealizované předpoklady. Poukázal na to, že po každé měsíční generaci, počet párů králíků se zvýšil z 1 do 2 do 3 do 5 do 8 do 13, atd., a zjistil, jak sledu postupoval přidáním předchozí dva termíny (v matematických termínech, Fn = Fn-1 + Fn-2), sekvence, které by mohly teoreticky prodloužit na neurčito.,

pořadí, které bylo ve skutečnosti známo, že Indické matematiky od 6. Století, má mnoho zajímavé matematické vlastnosti, a mnoho důsledků a vztahů sekvence byly objeveny až o několik století Fibonacciho po smrti., Například, sekvence regeneruje se v některé překvapivé způsoby: každý třetí F-číslo je dělitelné 2 (F3 = 2), každý čtvrtý F-číslo je dělitelné 3 (F4 = 3), každý pátý F-číslo je dělitelné 5 (F5 = 5), každý šestý F-číslo je dělitelné 8 (F6 = 8), každý sedmý F-číslo je dělitelné 13 (F7 = 13), atd., Čísla sekvence bylo také zjištěno, že být všudypřítomné v přírodě: mimo jiné, mnoho druhů kvetoucích rostlin mají čísla lístků ve Fibonacciho Posloupnosti; spirálové uspořádání ananas se vyskytují v 5s a 8s, ty šišky v 8s a 13ky, a semena slunečnice hlavy v 21, 34, 55, nebo i vyšší, termíny v pořadí; atd.,

Zlatý řez φ

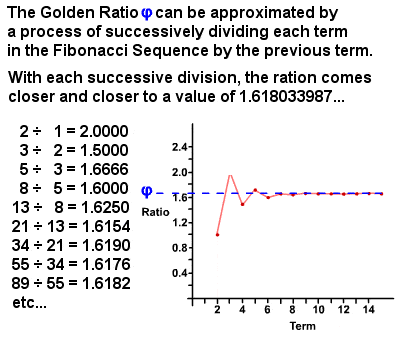
Zlatý řez φ lze odvodit z Fibonacciho Posloupnosti.

V 1750s, Robert Simson poznamenat, že poměr každý člen ve Fibonacciho Posloupnosti k předchozím období přístupy, s ještě větší přesností vyšší podmínky, poměru přibližně 1 : 1.6180339887 (to je vlastně iracionální číslo, které se rovná (1 + √5)⁄2, který se od té doby počítá na tisíce desetinných míst)., Tato hodnota je označována jako zlatý poměr, také známý jako zlatý průměr, Zlatý řez, božský podíl atd., a je obvykle označován řeckým písmenem phi φ (nebo někdy velkým písmenem Phi Φ). V podstatě jsou dvě množství ve zlatém poměru,pokud se poměr součtu množství k většímu množství rovná poměru většího množství k menšímu. Zlatý Poměr sám o sobě má mnoho jedinečné vlastnosti, jako je 1⁄φ = φ – 1 (0.618…) a φ2 = φ + 1 (2.618…), a existuje nespočet příklady to lze nalézt jak v přírodě a v lidském světě.,

obdélník se stranami v poměru 1 : φ je známý jako Zlatý Obdélník, a mnoho umělců a architektů v celé historii (sahající do starověkého Egypta a Řecka, ale zvláště populární v Renesanční umění, Leonardo da Vinci a jeho současníci) proporcí jejich díla přibližně používat Zlatý Poměr a Zlaté Obdélníky, které jsou široce považovány za přirozeně esteticky. Oblouk spojující opačné body stále menších vnořených zlatých obdélníků tvoří logaritmickou spirálu, známou jako zlatá spirála., Zlatý Poměr Zlatá Spirála lze nalézt také v překvapivě vysoký počet případů, v Přírodě, z mušle na květiny rohy zvířat do lidských těl, aby bouřkové systémy k dokončení galaxií.,

Je třeba mít na paměti, ačkoli, že Fibonacciho Posloupnost byla ve skutečnosti jen velmi drobné prvek v „Liber Abaci“ – ve skutečnosti, pořadí obdržela pouze Fibonacciho jméno v roce 1877, když Eduouard Lucas se rozhodl mu vzdát hold tím, že pojmenování série po něm – a to Fibonacciho sám nebyl zodpovědný za identifikaci žádné zajímavé matematické vlastnosti posloupnosti, její vztah k Zlatá střední cesta a Zlaté Obdélníky a Spirály, atd.,

Mřížky Násobení

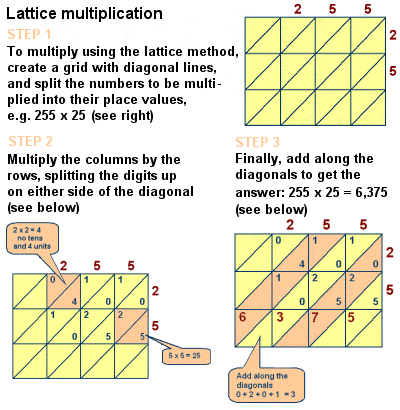
Fibonacciho představil příhradové násobení do Evropy

Nicméně, kniha je vliv na středověké matematiky je nepopiratelný, a to také zahrnuje diskusi o řadě dalších matematických problémů, jako je Čínská Věta o zbytcích, ideální čísla a prvočísla, vzorce pro aritmetickou řadu a na náměstí pyramidální čísla, Euklidovské geometrické důkazy a studie simultánní lineární rovnice v duchu Diophantus a Al-Karaji., Popsal také mříž (nebo síto) násobení metoda násobení velkých čísel, metoda – původně propagoval Islámských matematiků, jako Al-Khwarizmi – algoritmicky ekvivalentní dlouhé násobení.

nebyla ani „Liber Abaci“ Fibonacciho jediná kniha, i když to byla jeho nejdůležitější kniha., Jeho „Liber Quadratorum“ („Kniha Čtverce“), například, je kniha o algebře, publikoval v 1225, ve kterém se zobrazí prohlášení o tom, co se nyní nazývá Fibonacciho identity – někdy také známý jako Brahmagupta identity po mnohem dříve, Indický matematik, který také dospěl ke stejným závěrům – že součin dvou součtů dvou čtverců je sám součet dvou čtverců např. (12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,