Výsledky Učení
- seznámit se s historií poziční číselné soustavy
- Identifikovat základny, které byly použity v řadě systémů historicky
- Převést čísla mezi bází
- Použít dvě různé metody pro převod čísel mezi bází
Pozadí
Jak jste si možná představit, rozvoj základního systému je důležitým krokem v provádění procesu počítání efektivnější., Náš vlastní systém base-ten pravděpodobně vznikl ze skutečnosti, že máme 10 prstů (včetně palců) na dvou rukou. To je přirozený vývoj. Jiné civilizace však měly různé základny jiné než deset. Například domorodci z Queenslandu používali systém base-two, počítající takto: „jeden, dva, dva a jeden, dva dva, hodně.“Některé moderní jihoamerické kmeny mají základ-pět systém počítá tímto způsobem:“ jeden, dva, tři, čtyři, ruka, ruka a jeden, ruka a dva,“ a tak dále. Babyloňané používali základ-šedesát (sexigesimální) systém., V této kapitole se zabýváme konkrétním příkladem civilizace, která ve skutečnosti používala jiný základní systém než 10.
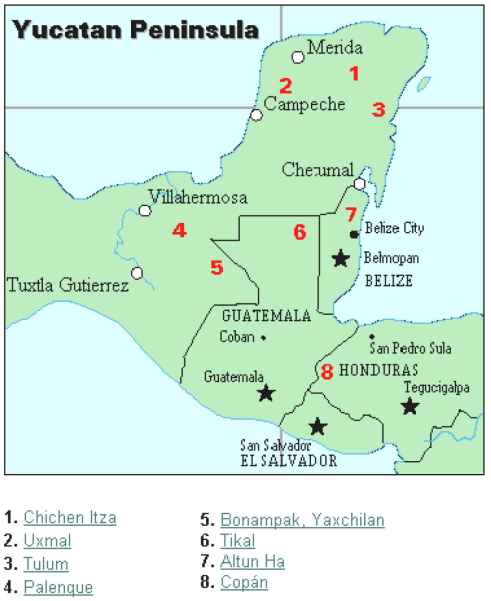 mayská civilizace je obecně datována od 1500 BCE do 1700 CE. Poloostrov Yucatan (viz obrázek 16) v Mexiku byl scénou pro vývoj jedné z nejpokročilejších civilizací starověkého světa. Mayové měli sofistikovaný rituální systém, na který dohlížela kněžská třída. Tato třída kněží vyvinula filozofii s časem jako božskou a věčnou., Kalendář a výpočty s ním spojené byly proto velmi důležité pro rituální život kněžské třídy, a tedy mayského lidu. Ve skutečnosti, hodně z toho, co víme o této kultuře pochází z jejich kalendářních záznamů a astronomických dat. Dalším důležitým zdrojem informací o Mayech jsou spisy otce Diega de Landa, který odešel do Mexika jako misionář v roce 1549.
mayská civilizace je obecně datována od 1500 BCE do 1700 CE. Poloostrov Yucatan (viz obrázek 16) v Mexiku byl scénou pro vývoj jedné z nejpokročilejších civilizací starověkého světa. Mayové měli sofistikovaný rituální systém, na který dohlížela kněžská třída. Tato třída kněží vyvinula filozofii s časem jako božskou a věčnou., Kalendář a výpočty s ním spojené byly proto velmi důležité pro rituální život kněžské třídy, a tedy mayského lidu. Ve skutečnosti, hodně z toho, co víme o této kultuře pochází z jejich kalendářních záznamů a astronomických dat. Dalším důležitým zdrojem informací o Mayech jsou spisy otce Diega de Landa, který odešel do Mexika jako misionář v roce 1549.
 Mayové vyvinuli dva číselné systémy—jeden pro obyčejné lidi a jeden pro kněze., Nejen, že tyto dva systémy používaly různé symboly, ale také používaly různé základní systémy. Pro kněze byl číselný systém řízen rituálem. Dny roku byli považováni za bohy, tak formální symboly pro dny byly zdobené hlavami, jako vzorek vlevo Od základní kalendář byl založen na 360 dní, kněžské číselná soustava používá smíšené základní systém zaměstnávání násobky 20 a 360. To vytváří matoucí systém, jehož podrobnosti přeskočíme.,/td>
Mayové vyvinuli dva číselné systémy—jeden pro obyčejné lidi a jeden pro kněze., Nejen, že tyto dva systémy používaly různé symboly, ale také používaly různé základní systémy. Pro kněze byl číselný systém řízen rituálem. Dny roku byli považováni za bohy, tak formální symboly pro dny byly zdobené hlavami, jako vzorek vlevo Od základní kalendář byl založen na 360 dní, kněžské číselná soustava používá smíšené základní systém zaměstnávání násobky 20 a 360. To vytváří matoucí systém, jehož podrobnosti přeskočíme.,/td>
The Mayan Number System
Instead, we will focus on the numeration system of the „common” people, which used a more consistent base system., Jak jsme již uvedli dříve, Mayové používali systém base – 20, nazývaný systém „vigesimal“. Stejně jako náš systém je Polohový, což znamená, že pozice číselného symbolu označuje jeho hodnotu místa. V následující tabulce můžete vidět hodnotu místa ve svislém formátu.
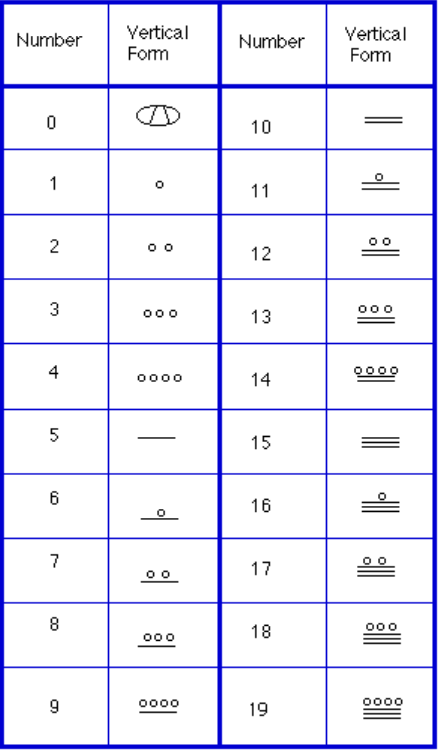
aby bylo možné zapisovat čísla, byly v tomto systému potřeba pouze tři symboly. Vodorovná lišta představovala množství 5, tečka představovala množství 1 a speciální symbol (považovaný za skořápku) představoval nulu., Mayský systém mohl být první, kdo využil nulu jako zástupný symbol / číslo. Prvních 20 čísel je uvedeno v tabulce vpravo.
Na rozdíl od našeho systému, kde se místo začíná vpravo a pak se pohybuje doleva, Mayské systémy umístí ty na dno vertikální orientace a pohybuje se nahoru, jak se zvyšuje hodnota místa.
když jsou čísla zapsána ve svislé podobě, nikdy by na jednom místě nemělo být více než čtyři tečky. Při psaní mayských čísel se každá skupina pěti teček stává jedním pruhem., Taky, nikdy by nemělo být více než tři bary na jednom místě … čtyři bary by byly převedeny na jednu tečku na dalším místě nahoru. Je to stejné jako 10 převedení na 1 na dalším místě, když nosíme během sčítání.
příklad
jaká je hodnota tohoto čísla, která je zobrazena ve svislé podobě?
Příklad:
Jaká je hodnota následujících Mayské číslo?,
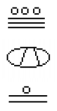
zkuste to
převést Mayské číslo níže na základnu 10.,

Příklad:
Převést základní 10 číslo 357510 na Mayské číslice.
psaní čísel se základnami většími než 10
když je základna čísla větší než 10, oddělte každou „číslici“ čárkou, aby bylo oddělení číslic jasné.
například v základně 20 napište číslo odpovídající 17 × 202 + 6 × 201 + 13 × 200, napíšeme 17,6,1320.
V následujícím videu představujeme další příklady, jak psát čísla pomocí Mayské číslice, stejně jako převod číslice psané v Mayské do základny 10 formě.,
Další video ukazuje další příklady převodu základních 10 čísel na Mayské číslice.
přidání mayských čísel
při přidávání mayských čísel dohromady přijmeme schéma, které Mayové pravděpodobně nepoužili, ale které nám usnadní život.
Příklad:
Přidat, v Mayské, čísla 37 a 29:

Zkuste přidat 174 a 78 v Mayské o první převod Mayských čísel a pak pracuje zcela v rámci tohoto systému. Nepřidávejte do základny-deset (desetinné číslo) až do samého konce, když zkontrolujete svou práci.
V posledním videu jsme se ukázat další příklady přidání Mayské číslice.,
V tomto modulu jsme stručně načrtli vývoj čísel a našeho počítacího systému s důrazem na“ krátkou “ část. Existuje mnoho zdrojů informací a výzkumu, které vyplňují mnoho svazků knih na toto téma. Bohužel, nemůžeme se přiblížit pokrytí všech informací, které jsou tam venku.

pouze jsme poškrábali povrch bohatství výzkumu a informací, které existují o vývoji čísel a počítání v celé lidské historii., Důležité je poznamenat, že systém, který používáme každý den, je produktem tisíce let pokroku a vývoje. Představuje příspěvky mnoha civilizací a kultur. Nespadá k nám z nebe, dar od bohů. Nejedná se o vytvoření vydavatele učebnic. Je to skutečně stejně lidské jako my, stejně jako zbytek matematiky. Za každým symbolem, vzorcem a pravidlem je lidská tvář, kterou je třeba najít, nebo alespoň hledat.
dále doufáme, že nyní máte základní ocenění za to, jak zajímavé a rozmanité číselné systémy mohou získat., Taky, jsme si docela jisti, že jste si také začali uvědomovat, že bereme náš vlastní číselný systém za samozřejmost natolik, že když se snažíme přizpůsobit se jiným systémům nebo základnám, ocitáme se skutečně museli soustředit a přemýšlet o tom, co se děje.







