v geometrii je polyhedron uzavřený prostor, jehož tváře jsou polygony. Slovo mnohostěn má řecký původ, což znamená mnoho tváří. Níže uvádíme několik příkladů polyhedry.
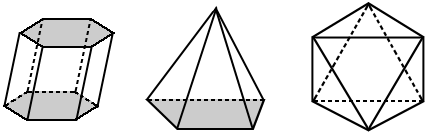
Charakteristika mnohostěnu
polygony, které tvoří mnohostěn se nazývá obličeje. Segmenty čáry vytvořené dvěma protínajícími se plochami se nazývají hrany. Vrcholy jsou body, kde se setkávají tři nebo více okrajů.,
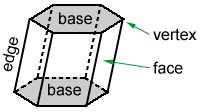
šestiúhelníkový hranol výše je mnohostěn, který má 6 boční plochy, které jsou rovnoběžníky, a 2 plochy na horní a dolní, tzv. bází, které jsou šestiúhelníky.
Eulerova věta
Eulerova věta ukazuje vztah mezi počtem ploch, vrcholů a hran mnohostěn., To stanoví, že součet ploch a vrcholů minus počet hran, se vždy rovná dvěma.
F + V – E = 2
kde F je počet ploch, V je počet vrcholů a E je počet hran mnohostěnu.
Příklad:
Pro šestibokého hranolu je uvedeno výše, F = 8 (šest boční plochy + dvě základny), V = 12, E = 18:
8 + 12 – 18 = 2
Klasifikace mnohostěnů
Mnohostěnů mohou být klasifikovány mnoha způsoby. Mohou být například klasifikovány jako pravidelná a nepravidelná polyhedra., Pravidelný polyhedron je polyhedron, jehož tváře jsou všechny shodné pravidelné polygony; jakýkoli polyhedron, který nesplňuje tyto podmínky, je považován za nepravidelný.
Polyhedra lze také klasifikovat jako konvexní a konkávní. Konkávní mnohostěn má alespoň jednu tvář, která je konkávní mnohoúhelník. Polyhedron, který není konkávní, je konvexní. Polyhedra lze také klasifikovat na základě počtu tváří, které má. Například čtyřstěn má 4 tváře, pentahedron má 5 tváří a hexahedron má 6 tváří.,
níže je uveden seznam termínů, které se často používají k popisu polyhedry na základě jejich charakteristik.
hranoly
hranoly jsou polyhedra, které mají dvě shodné tváře, nazývané základny, ležící v paralelních rovinách. Hranol je obvykle pojmenován podle tvaru jeho polygonálních základen. Boční plochy (strany, které nejsou základnami) jsou rovnoběžníky, obdélníky nebo čtverce.,
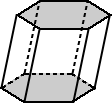
| Pravidelné prism | Nepravidelný hranol |
|---|---|
 |
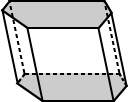 |
| Základy pro pravidelného šestibokého hranolu výše základny, které jsou pravidelné šestiúhelníky. | základy pro hexagonální hranol výše jsou nepravidelný šestiúhelník. |
pyramidy
pyramidy jsou mnohoúhelník, který má jako svou základnu a trojúhelníky jako všechny ostatní tváře.Pyramida je také obvykle pojmenována podle tvaru jeho polygonální základny.,
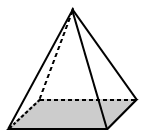
| Pravidelné pyramidy | Nepravidelné pyramidy |
|---|---|
 |
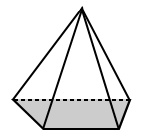 |
| Základní čtvercové pyramidy výše má základnu, která je čtverec (pravidelný mnohoúhelník). | základem pro lichoběžníkovou pyramidu výše je lichoběžník s nerovnými stranami (jedná se tedy o nepravidelný mnohoúhelník). |
Regular polyhedra
pravidelný polyhedron je polyhedron, jehož tváře jsou všechny shodné, pravidelné polygony., Pravidelný mnohostěn je pojmenován na základě počtu tváří. Existuje pouze pět polyhedra, které jsou pravidelné polyhedra; tyto jsou označovány jako platonické pevné látky.
pět Platonické pevné látky
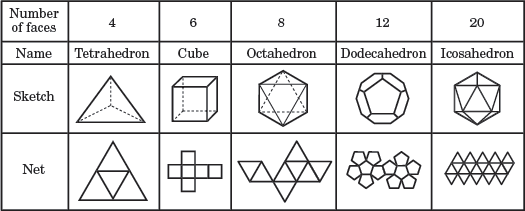
V diagramu výše, každý pravidelný mnohostěn je jmenován na základě jeho počet ploch. Síť pod každým náčrtem ukazuje 2D obraz všech tváří mnohostěnu.
většina pravidelných hranolů se obecně nepovažuje za pravidelnou polyhedru., Kostka je jediný pravidelný hranol, který lze také klasifikovat jako pravidelný mnohostěn.
Podobně, pravidelný čtyřstěn je pouze pravidelné pyramidy, která je také pravidelný mnohostěn.