the 5 Clustering algoritmy data vědci potřebují vědět

nedávno jsem začal vzdělávací bulletin zaměřený na knihu. Book Dives je bi-týdenní newsletter, kde pro každé nové vydání se ponoříme do non-fiction knihy. Dozvíte se o základních lekcích Knihy a o tom, jak je aplikovat v reálném životě. Můžete se přihlásit k odběru zde.

Clustering je technika strojového učení, která zahrnuje seskupení datových bodů. Vzhledem k souboru datových bodů můžeme použít algoritmus shlukování pro klasifikaci každého datového bodu do konkrétní skupiny., Teoreticky by datové body, které jsou ve stejné skupině, měly mít podobné vlastnosti a/nebo vlastnosti, zatímco datové body v různých skupinách by měly mít vysoce odlišné vlastnosti a/nebo vlastnosti. Clustering je metoda bez dozoru učení a je běžnou technikou pro statistickou analýzu dat používanou v mnoha oblastech.

V Data Science, můžeme použít clustering analýzy získat nějaké cenné poznatky z našich dat tím, že vidí, jaké skupiny datových bodů na podzim, když jsme se použít clustering algoritmus., Dnes se podíváme na 5 populárních algoritmů shlukování, které vědci dat potřebují znát, a jejich klady a zápory!

K-znamená shlukování

k-prostředky je pravděpodobně nejznámější clustering algoritmus. Vyučuje se v mnoha úvodních třídách vědy o datech a strojového učení. Je to snadné pochopit a implementovat v kódu! Podívejte se na grafiku níže pro ilustraci.,

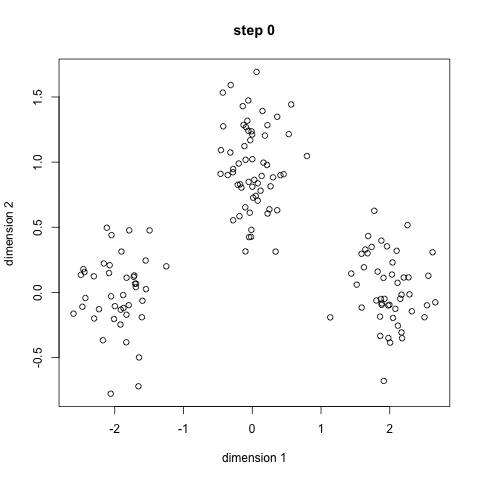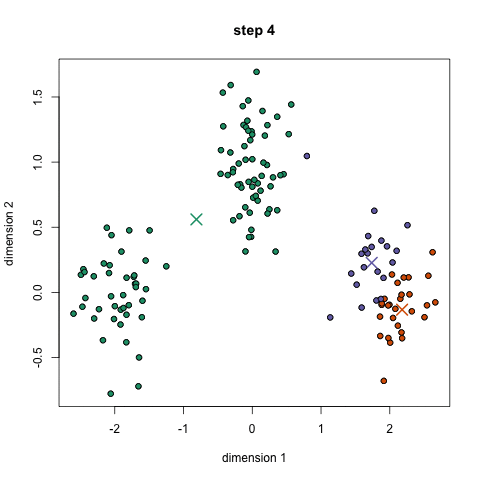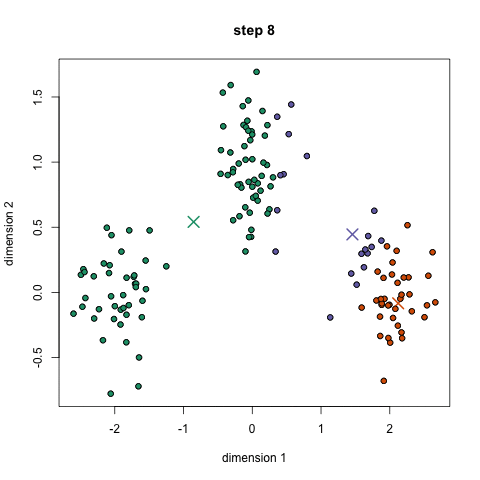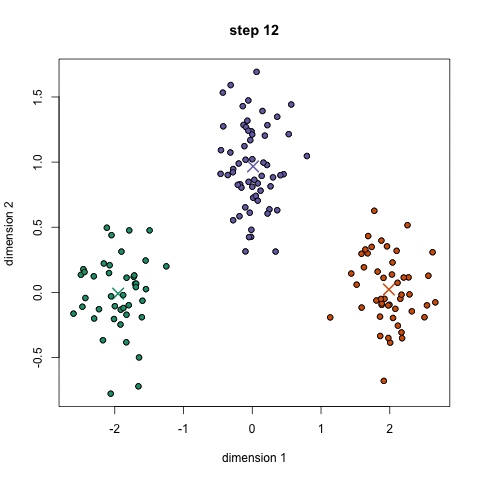
1. Na začátku, jsme nejprve vyberte počet tříd/skupin použití a náhodně inicializovat jejich středové body. Chcete-li zjistit počet tříd, které chcete použít, je dobré se rychle podívat na data a pokusit se identifikovat jakákoli odlišná seskupení. Středové body jsou vektory stejné délky jako každý vektor datového bodu a jsou“ X “ ve výše uvedené grafice.,
2. Každý datový bod je klasifikován podle výpočtu vzdálenosti mezi tímto bodem a každá skupina střed, a pak se zařazuje bod být ve skupině, jehož střed je nejblíže.
3. na základě těchto klasifikovaných bodů přepočítáme centrum skupiny tím, že vezmeme průměr všech vektorů ve skupině.
4. opakujte tyto kroky pro nastavený počet iterací nebo dokud se centra skupin mezi iteracemi příliš nezmění. Můžete se také rozhodnout náhodně inicializovat skupinová centra několikrát a poté vybrat běh, který vypadá, že poskytuje nejlepší výsledky.,

K-Znamená, má tu výhodu, že je to docela rychlé, protože vše, co děláme, je výpočet vzdálenosti mezi body a skupiny center; velmi málo výpočty! Má tedy lineární složitost O (n).

Na druhé straně má k-Means několik nevýhod. Nejprve musíte vybrat, kolik skupin / tříd existuje. To není vždy triviální a ideálně se shlukovacím algoritmem bychom chtěli, aby to pro nás přišlo, protože smyslem je získat nějaký vhled z dat., K-znamená také začíná s náhodným výběrem clusteru center, a proto to může přinést různé shlukování výsledků na různých běhů algoritmu. Výsledky tedy nemusí být opakovatelné a nemají konzistenci. Jiné metody clusteru jsou konzistentnější.

K-Mediánů je další clustering algoritmus týkající se K-means, s výjimkou toho, přepočítání skupina centru bodů pomocí průměru použijeme medián vektorové skupiny., Tato metoda je méně citlivá na odlehlé hodnoty (kvůli použití mediánu), ale je mnohem pomalejší pro větší datové sady, protože třídění je vyžadováno při každé iteraci při výpočtu mediánového vektoru.

Mean-Shift, Clustering

shift clustering je posuvné-okna-based algoritmus, který se pokouší najít husté oblasti datových bodů. To je těžiště založených na algoritmu, což znamená, že cílem je najít střed bodů z každé skupiny/třídy, který funguje po aktualizaci kandidáty na centrum body průměr body v rámci posuvné-okna., Tyto kandidáta windows, jsou pak filtrovány v post-fázi zpracování k odstranění blízkosti-duplikáty, které tvoří konečnou množinu centru bodů a jejich odpovídající skupiny. Podívejte se na grafiku níže pro ilustraci.

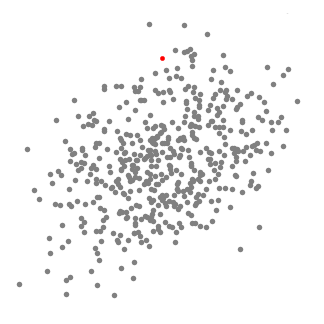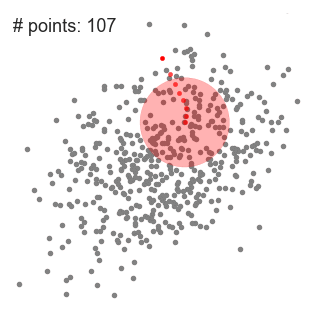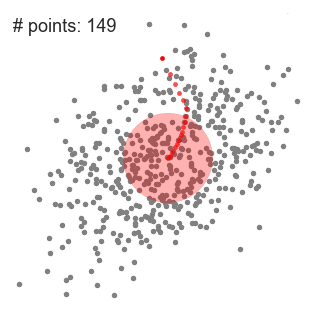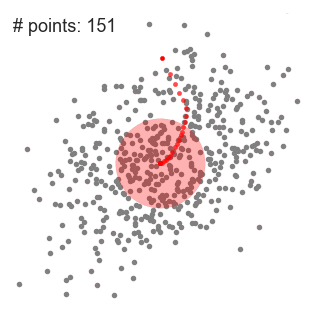
1. vysvětlit mean-shift budeme uvažovat množinu bodů v dvourozměrném prostoru jako výše uvedené ilustrace., Začínáme kruhovým posuvným oknem vystředěným v bodě C (náhodně vybrané) a s poloměrem r jako jádrem. Střední posun je algoritmus horolezectví, který zahrnuje iterativní přesun tohoto jádra do oblasti s vyšší hustotou na každém kroku až do konvergence.
2. při každé iteraci je posuvné okno posunuto směrem k oblastem s vyšší hustotou posunutím středového bodu na průměr bodů v okně (odtud název). Hustota v posuvném okně je úměrná počtu bodů uvnitř., Přirozeně se posunutím na průměr bodů v okně postupně přesune do oblastí s vyšší bodovou hustotou.
3. posuvné okno pokračujeme posouváním podle průměru, dokud není žádný směr, ve kterém může posun pojmout více bodů uvnitř jádra. Podívejte se na grafiku výše; pokračujeme v pohybu kruhu, dokud již nezvyšujeme hustotu (tj. počet bodů v okně).
4. tento proces kroků 1 až 3 se provádí s mnoha posuvnými okny, dokud všechny body neleží v okně., Když se více posuvných oken překrývá, okno obsahující nejvíce bodů je zachováno. Datové body jsou pak seskupeny podle posuvného okna, ve kterém jsou umístěny.

obrázek celého procesu od konce do konce se všemi posuvnými okny je uveden níže. Každá černá tečka představuje střed posuvného okna a každá šedá tečka je datový bod.,

Na rozdíl od K-means clustering, není nutné vyberte číslo, které klastrů jako mean-shift se automaticky objeví. To je obrovská výhoda. Skutečnost, že centra klastru se sbíhají k bodům maximální hustoty, je také docela žádoucí, protože je docela intuitivní pochopit a dobře zapadá do přirozeně datově řízeného smyslu., Nevýhodou je, že výběr velikosti okna /poloměru “ r “ může být netriviální.

prostorové shlukování aplikací založených na hustotě s hlukem (DBSCAN)

DBSCAN je seskupený algoritmus založený na hustotě podobný střední směně, ale s několika významnými výhodami. Podívejte se na další efektní grafiku níže a začněme!,

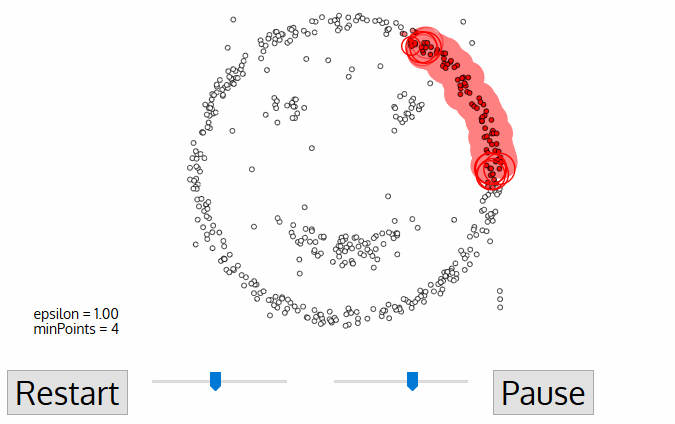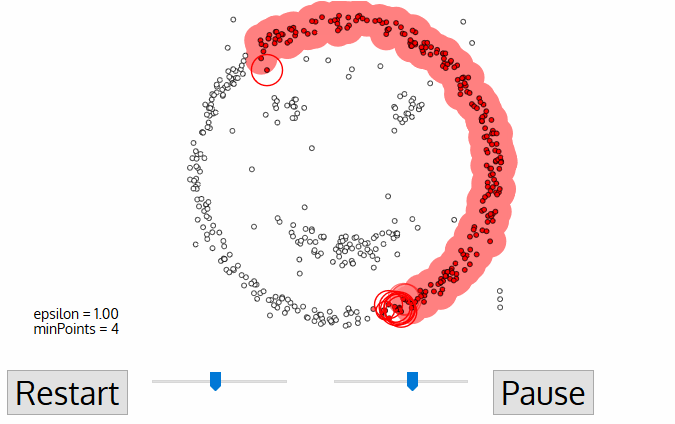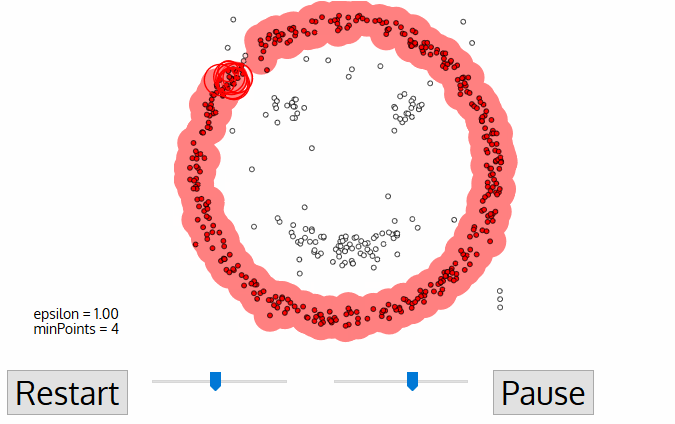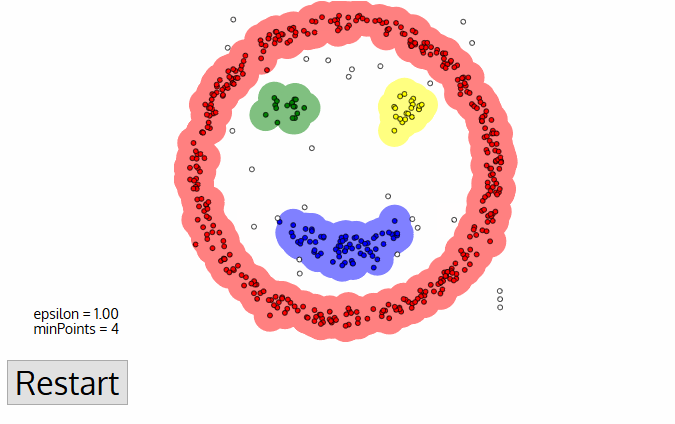
1. DBSCAN začíná libovolný výchozí datový bod, který nebyl navštívil. Sousedství tohoto bodu se extrahuje pomocí vzdálenosti epsilon ε (všechny body, které jsou ve vzdálenosti ε, jsou sousedské body).,
2. pokud je v tomto sousedství dostatečný počet bodů (podle minpointů), spustí se proces shlukování a aktuální datový bod se stane prvním bodem v novém clusteru. V opačném případě bude bod označen jako šum (později se tento hlučný bod může stát součástí clusteru). V obou případech je tento bod označen jako „navštívený“.
3. pro tento první bod v novém clusteru se body v jeho sousedství ε distance také stávají součástí stejného clusteru., Tento postup, aby všechny body v ε okolí patří do stejného clusteru se pak opakuje pro všechny nové body, které byly právě přidány do skupiny clusteru.
4. tento proces kroků 2 a 3 se opakuje, dokud nejsou určeny všechny body v clusteru, tj. všechny body v sousedství ε clusteru byly navštíveny a označeny.
5. Jakmile jsme hotovi s aktuální clusteru, nové nenavštívené bod je získán a zpracován, což vede k objevení dalšího clusteru nebo hluk. Tento proces se opakuje, dokud nejsou všechny body označeny jako navštívené., Protože na konci toho byly všechny body navštíveny, každý bod bude označen jako buď patřící do clusteru, nebo jako hluk.

DBSCAN představuje některé velké výhody oproti jiným algoritmům shlukování. Za prvé, nevyžaduje pe-set počet klastrů vůbec. Identifikuje také odlehlé hodnoty jako zvuky, na rozdíl od střední směny, která je jednoduše hodí do clusteru, i když je datový bod velmi odlišný. Navíc může najít libovolně velké a libovolně tvarované klastry docela dobře.,

hlavní nevýhodou DBSCAN je to, že nevykonává stejně jako ostatní, když jsou klastry s různou hustotou. Je to proto, že nastavení prahu vzdálenosti ε a minpointů pro identifikaci sousedních bodů se bude lišit od clusteru k clusteru, když se hustota mění. K této nevýhodě dochází také u velmi vysoce dimenzionálních dat, protože práh vzdálenosti ε se opět stává náročným odhadem.,

shlukování očekávání–maximalizace (EM) pomocí Gaussovských modelů směsí (GMM)

jednou z hlavních nevýhod K-prostředků je naivní použití střední hodnoty pro centrum clusteru. Vidíme, proč to není nejlepší způsob, jak dělat věci tím, že se podíváme na obrázek níže. Na levé straně, vypadá to docela zřejmé, pro lidské oko, že tam jsou dva kruhové shluky s různým poloměrem‘ na střed na stejný průměr. K-Znamená to nemůže zvládnout, protože střední hodnoty klastrů jsou velmi blízko u sebe., K-Means také selže v případech, kdy klastry nejsou kruhové, opět v důsledku použití průměru jako centra clusteru.

Gaussian Mixture Models (Gmm), dát nám větší flexibilitu než K-means. S GMMs předpokládáme, že datové body jsou Gaussian distribuovány; to je méně restriktivní předpoklad, než říkat, že jsou kruhové pomocí průměru., Tímto způsobem máme dva parametry, které popisují tvar klastrů: střední a směrodatná odchylka! Vezmeme-li příklad ve dvou rozměrech, znamená to, že klastry mohou mít jakýkoli druh eliptického tvaru (protože máme směrodatnou odchylku ve směrech x I y). Každá Gaussovská distribuce je tedy přiřazena k jednomu clusteru.

pro nalezení parametrů Gaussian pro každý cluster (např. střední a směrodatná odchylka) použijeme optimalizační algoritmus nazvaný Expectation–Maximization (EM)., Podívejte se na grafiku níže jako ilustraci Gaussians jsou namontovány do klastrů. Pak můžeme pokračovat v procesu shlukování očekávání a maximalizace pomocí GMM.

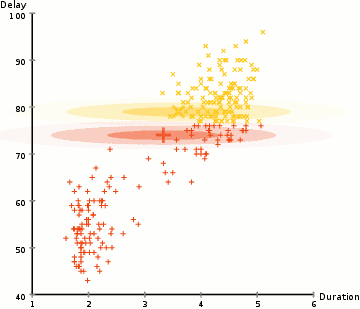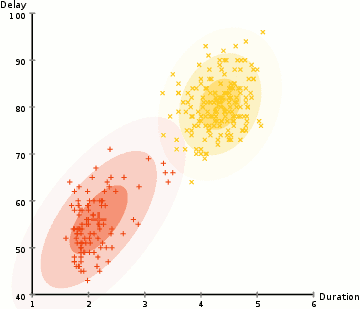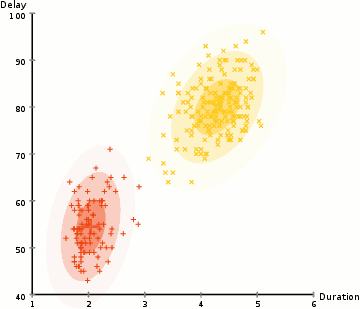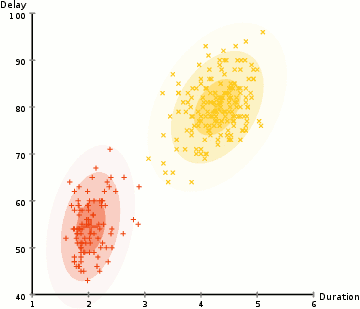
1. Začneme tím, že vyberete počet klastrů (jako K-means) a náhodně inicializace Gaussovo rozdělení, parametry pro každý shluk., Jeden může pokusit poskytnout dobrý odhad pro počáteční parametry tím, že se rychle podívat na data příliš. Ačkoli poznámka, jak je vidět na obrázku výše, to není 100% nutné, protože Gaussové začínají jako velmi chudí, ale jsou rychle optimalizováni.
2. vzhledem k těmto gaussovským distribucím pro každý klastr Vypočítejte pravděpodobnost, že každý datový bod patří do určitého klastru. Čím blíže je bod k Gaussovu středu, tím je pravděpodobnější, že patří do tohoto klastru., To by mělo dávat smysl, protože s Gaussovo rozdělení, předpokládáme, že většina dat leží blíže k centru hvězdokupy.
3. na Základě těchto hodnot můžeme vypočítat nové parametry pro Gaussovo rozdělení takové, že jsme maximalizovat pravděpodobnost datových bodů v rámci klastrů. Tyto nové parametry vypočítáváme pomocí váženého součtu pozic datových bodů, kde váhy jsou pravděpodobnosti datového bodu patřícího do tohoto konkrétního klastru., Abychom to vysvětlili vizuálně, můžeme se podívat na grafiku výše, zejména na žlutý cluster jako příklad. Distribuce začíná náhodně při první iteraci, ale vidíme, že většina žlutých bodů je napravo od této distribuce. Když vypočítáme součet vážený pravděpodobnostmi, i když v blízkosti středu jsou některé body, většina z nich je vpravo. Průměr distribuce je tedy přirozeně posunut blíže k množině bodů. Můžeme také vidět, že většina bodů je „zprava dolů doleva“., Proto je směrodatná odchylka změny k vytvoření elipsy, která je více vybavena, aby tyto body, aby se maximalizoval součet vážený pravděpodobností.
4. kroky 2 a 3 se opakují iterativně až do konvergence, kde se distribuce příliš nemění z iterace na iteraci.

existují 2 klíčové výhody používání GMM. Za prvé GMM jsou mnohem pružnější, pokud jde o cluster kovariance než k-prostředky; vzhledem k parametru směrodatné odchylky, klastry mohou mít jakýkoli tvar elipsy, spíše než být omezeny na kruhy., K-Means je vlastně zvláštní případ GMM, ve kterém se kovariance každého klastru podél všech rozměrů blíží 0. Za druhé, protože GMM používají pravděpodobnosti, mohou mít více klastrů na datový bod. Takže pokud je datový bod uprostřed dvou překrývajících se klastrů, můžeme jednoduše definovat jeho třídu tím, že patří X-procent do třídy 1 a Y-procent do třídy 2. I. E GMMs podporují smíšené členství.

Aglomerativní hierarchické shlukování

hierarchické clusteringové algoritmy spadají do 2 kategorií: shora dolů nebo zdola nahoru., Bottom-up algoritmů léčit každý datový bod jako jeden cluster na začátku, a pak postupně sloučit (nebo aglomerát) dvojice klastrů, dokud se všechny shluky byly sloučeny do jediného clusteru, který obsahuje všechny datové body. Hierarchické shlukování zdola nahoru se proto nazývá hierarchické aglomerativní shlukování nebo HAC. Tato hierarchie klastrů je reprezentována jako strom (nebo dendrogram). Kořen stromu je jedinečný shluk, který shromažďuje všechny vzorky, listy jsou shluky pouze s jedním vzorkem., Podívejte se na obrázek níže pro ilustraci před přechodem na algoritmus kroků,

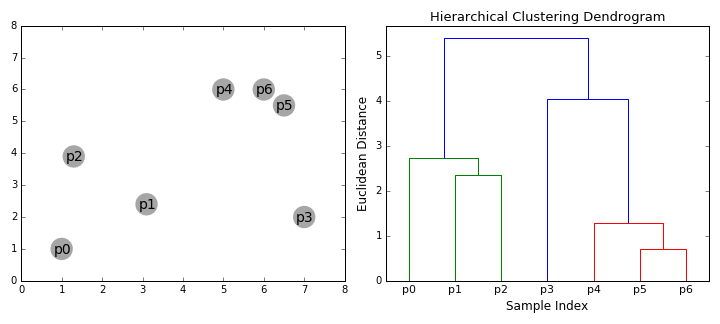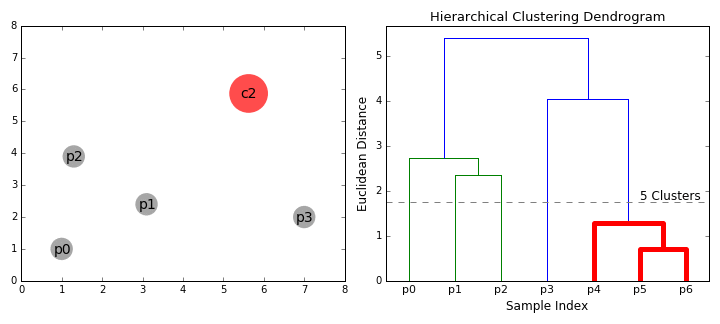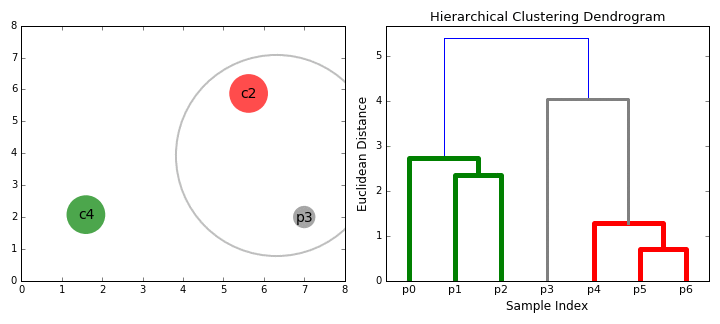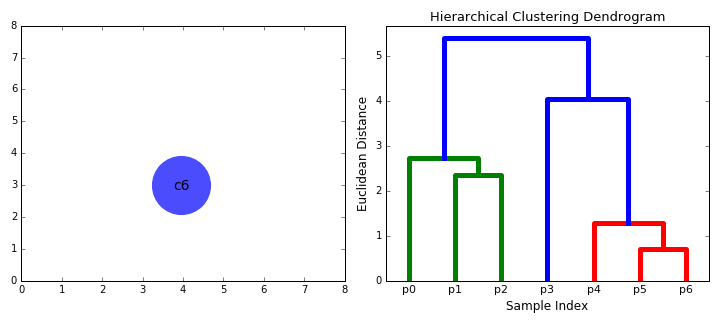
1. začneme tím, že zachází každý datový bod jako jeden cluster i.e jsou-li X datových bodů v náš dataset pak máme X klastrů. Poté vybereme metriku vzdálenosti, která měří vzdálenost mezi dvěma klastry., Jako příklad použijeme průměrné propojení, které definuje vzdálenost mezi dvěma klastry jako průměrnou vzdálenost mezi datovými body v prvním klastru a datovými body ve druhém klastru.
2. při každé iteraci spojujeme dva klastry do jednoho. Obě klastry, které mají být kombinovány, jsou vybrány jako ty s nejmenším průměrným spojením. Tj. podle naší vybrané metriky vzdálenosti mají tyto dva klastry nejmenší vzdálenost mezi sebou, a proto jsou nejpodobnější a měly by být kombinovány.
3. Krok 2 se opakuje, dokud nedosáhneme kořene stromu i.,e máme pouze jeden cluster, který obsahuje všechny datové body. Tímto způsobem si můžeme vybrat, kolik klastrů chceme nakonec, jednoduše výběrem, kdy přestat kombinovat klastry, tj. když přestaneme stavět strom!

Hierarchické shlukování nevyžaduje nám zadat počet shluků a můžeme si dokonce vybrat, které číslo klastrů vypadá nejlépe, protože budujeme strom. Navíc algoritmus není citlivý na výběr metriky vzdálenosti; všechny mají tendenci pracovat stejně dobře, zatímco u jiných algoritmů shlukování je rozhodující volba metriky vzdálenosti., Obzvláště dobrým případem použití hierarchických metod shlukování je, když základní data mají hierarchickou strukturu a chcete obnovit hierarchii; jiné algoritmy shlukování to nemohou udělat. Tyto výhody hierarchického shlukování přicházejí za cenu nižší účinnosti, protože má časovou složitost O(n3), na rozdíl od lineární složitosti k-prostředků a GMM.