5 Klusterointi Algoritmit Tietoa Tutkijoiden Täytyy Tietää

olen viime aikoina alkanut kirja-keskittynyt koulutus-uutiskirje. Kirjadives on kahden viikon välein ilmestyvä tiedote, jossa jokaisesta uudesta numerosta sukelletaan tietokirjaan. Opit kirjan ydintunneista ja niiden soveltamisesta tosielämässä. Voit tilata sen täältä.

Klusterointi on Kone-Oppimisen tekniikka, joka sisältää ryhmittely tietojen pistettä. Kun otetaan huomioon joukko datapisteitä, Voimme käyttää klusterointialgoritmia luokittelemaan jokaisen datapisteen tiettyyn ryhmään., Teoriassa, tietojen pistettä, jotka ovat samassa ryhmässä pitäisi olla samanlaisia ominaisuuksia ja/tai piirteitä, kun tietoja pistettä eri ryhmien tulisi olla erittäin erilaisia ominaisuuksia ja/tai piirteitä. Clustering on menetelmä, jota ei valvota, ja se on yleinen menetelmä tilastotietojen analysoinnissa, jota käytetään monilla aloilla.

Datatieteessä voimme hyödyntää klusterianalyysia saadaksemme arvokasta tietoa datastamme näkemällä, mihin ryhmiin datapisteet kuuluvat, kun käytämme klusterointialgoritmia., Tänään, aiomme tarkastella 5 suosittu klusterointi algoritmeja, että data tutkijat täytyy tietää ja niiden hyvät ja huonot puolet!

K-Means Clustering

K-Means on luultavasti tunnetuin klusterointialgoritmi. Sitä opetetaan paljon johdantotieteen ja koneoppimisen tunneilla. Se on helppo ymmärtää ja toteuttaa koodilla! Katso havainnekuva alla olevasta grafiikasta.,

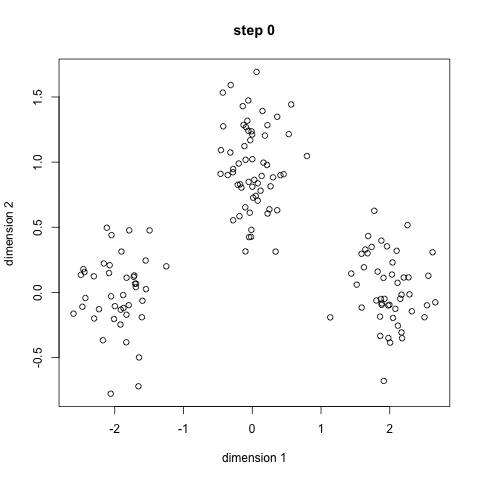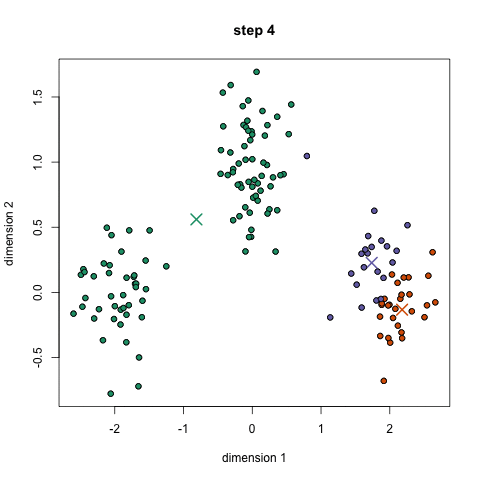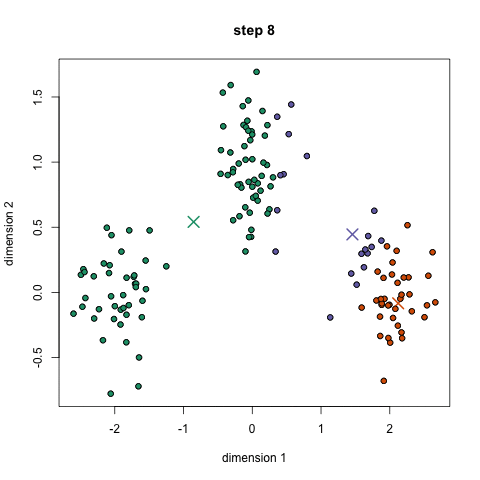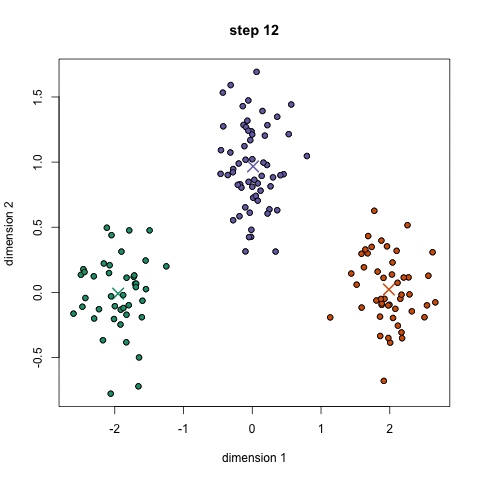
1. aloita meidän on ensin valita useita luokkia/ryhmiä, käyttää ja satunnaisesti alustaa niiden keskellä pistettä. Jos haluat selvittää, kuinka monta luokkaa käyttää, on hyvä vilkaista tietoja nopeasti ja yrittää tunnistaa kaikki erilliset ryhmittymät. Keskus pistettä vektorit ovat samanpituisia kuin jokainen datapiste vektori ja ”X: n” graafinen edellä.,
2. Jokainen datapiste luokitellaan laskemalla sen etäisyys, että pisteen ja jokainen ryhmä keskellä, ja sitten luokittelussa kohta olla ryhmä, jonka keskipiste on lähimpänä sitä.
3. näiden luokiteltujen pisteiden perusteella korjaamme ryhmäkeskusta ottamalla kaikkien ryhmän vektorien keskiarvon.
4. Toista nämä vaiheet, asettaa toistojen tai kunnes ryhmä keskuksia, ei muutos paljon välillä toistojen. Voit myös valita satunnaisesti alustaa ryhmän keskuksia muutaman kerran, ja valitse sitten ajaa, joka näyttää siltä, että se antoi parhaat tulokset.,

K-means on se etu, että se on melko nopea, koska kaikki me todella tehdä, on laskeminen etäisyydet pisteiden välillä ja ryhmän keskukset; hyvin vähän laskelmat! Se on siten lineaarinen monimutkaisuus O (n).

toisaalta K-keinolla on pari haittaa. Ensinnäkin, sinun täytyy valita, kuinka monta ryhmää / luokkia on. Tämä ei ole aina triviaalia ja mieluiten klusterointi algoritmi haluaisimme selvittää ne pois, koska kohta se on saada jonkinlainen käsitys aineistosta., K-means alkaa myös satunnainen valinta klusteri keskukset ja siksi se saattaa tuottaa eri klustereiden tuloksia eri ajojen algoritmi. Tulokset eivät siis välttämättä ole toistettavissa, eivätkä ne ole johdonmukaisia. Muut klusterimenetelmät ovat johdonmukaisempia.

K-Keskuksia on toinen klusterointi algoritmi liittyvät K-means, paitsi sen sijaan recomputing ryhmä center pistettä käyttäminen tarkoittaa, että emme käytä mediaani vektori ryhmä., Tämä menetelmä on vähemmän herkkä poikkeaville havainnoille (koska käyttämällä Mediaani), mutta on paljon hitaampaa suurempia datajoukkoja, kuten lajittelu on pakollinen jokaisen iteraation laskettaessa Mediaani vektori.

Mean-Shift Klusterointi

Mean shift klusterointi on liukuva-ikkuna-pohjainen algoritmi, joka yrittää löytää tiheä alueilla tiedot pistettä. Se on centroid-pohjainen algoritmi tarkoittaa, että tavoite on paikantaa center pistettä kunkin ryhmän/luokan, joka toimii päivittämällä ehdokkaita center-pisteiden keskiarvo pisteiden sisällä liukuva-ikkuna., Nämä ehdokas ikkunat ovat sitten suodatetaan post-processing-vaiheessa poistamaan lähes kaksoiskappaleet, muodostaen lopullinen joukko center pistettä ja niiden vastaavat ryhmät. Katso havainnekuva alla olevasta grafiikasta.

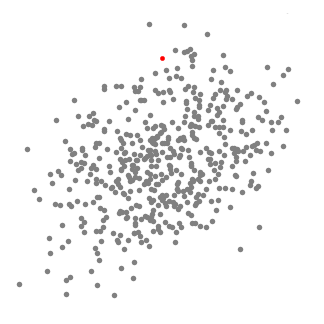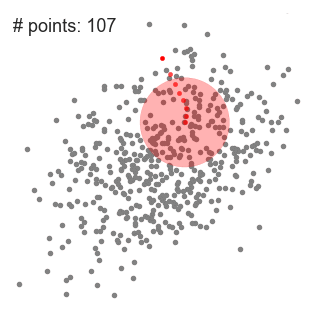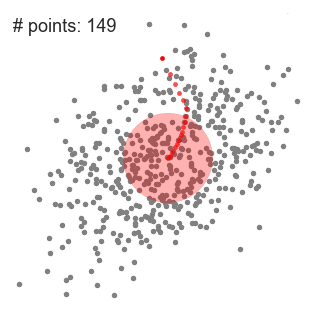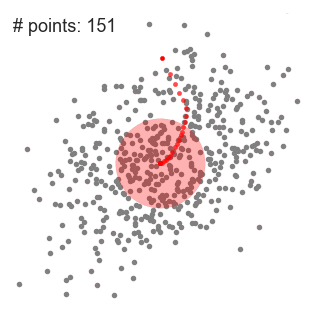
1. selittää mean-shift harkitsemme joukko pisteitä kaksiulotteisessa avaruudessa, kuten edellä kuva., Aloitamme pyöreällä liukuikkunalla, jonka keskipisteenä on piste C (satunnaisesti valittu) ja jonka säde r on ydin. Siis vaihto on hill-climbing-algoritmi, joka liittyy siirtymässä tämän ytimen iteratiivisesti suurempi tiheys alueella kukin vaihe, kunnes lähentymistä.
2. jokaisen iteraation, liukuva ikkuna on siirtynyt kohti alueiden suurempi tiheys siirtämällä keskus piste tarkoittaa pistettä ikkunan sisällä (siitä nimi). Liukuikkunan tiheys on verrannollinen sen sisällä olevien pisteiden määrään., Siirtymällä ikkunan pisteiden keskiarvoon se siirtyy luonnollisesti vähitellen kohti suurempia pistetiheyksiä.
3. Olemme edelleen siirtymässä liukuikkuna mukaan tarkoita sitä, kunnes ei ole suunnasta, johon muutos mahtuu enemmän pistettä sisällä ydin. Tutustu graafinen edellä; me liikkuvat ympyrän, kunnes emme enää tihentämällä (en.e määrä pisteitä ikkunassa).
4. tämä vaiheiden 1-3 prosessi tehdään monilla liukuikkunoilla, kunnes kaikki kohdat ovat ikkunan sisällä., Kun useita liukuikkunoita päällekkäin ikkuna, joka sisältää eniten pisteitä, säilyy. Tämän jälkeen datapisteet ryhmitellään Liukuikkunan mukaan, jossa ne sijaitsevat.

alla on havainnekuva koko prosessista päästä päähän kaikilla liukuikkunoilla. Jokainen musta piste edustaa Liukuikkunan centroidia ja jokainen harmaa piste on datapiste.,

Toisin kuin K-means klusterointi, ei tarvitse valita useita klustereita, kuten keskiarvo-shift automaattisesti havaitsee tämän. Se on valtava etu. Se, että klusteri keskukset lähentyvät kohti pistettä maksimi tiheys on myös erittäin toivottavaa, koska se on melko intuitiivinen ymmärtää, ja sopii hyvin luonnollisesti data-driven mielessä., Haittapuoli on, että valinta ikkunan koko / säde ” r ” voi olla ei-triviaali.

Density-Based Spatial Clustering Sovelluksia Melu (DBSCAN)

DBSCAN on tiheys-pohjainen aihekokonaisuuksien algoritmi samanlainen mean-shift, mutta pari merkittäviä etuja. Katso toinen hieno graafinen alla ja aloitetaan!,

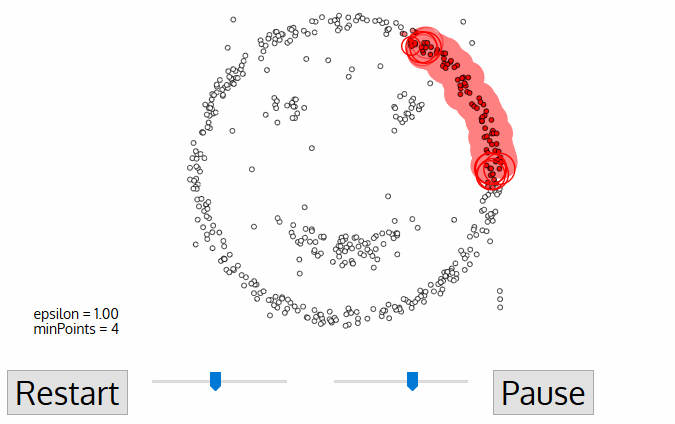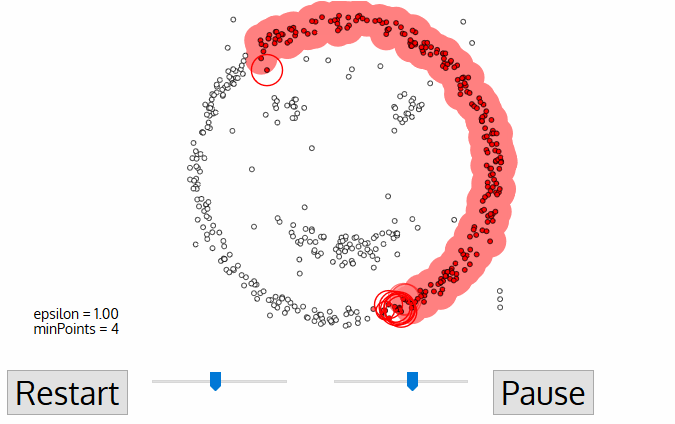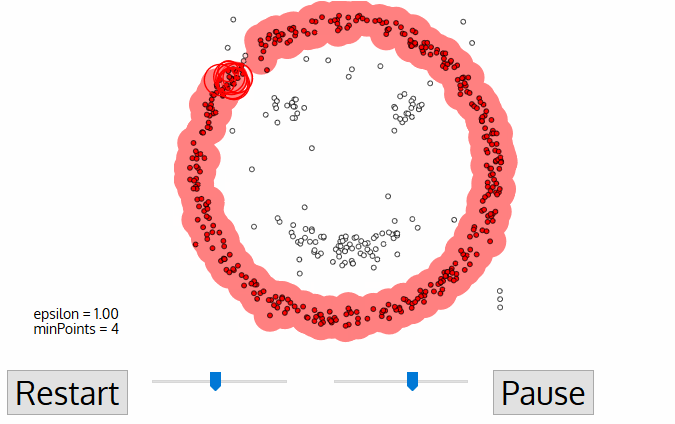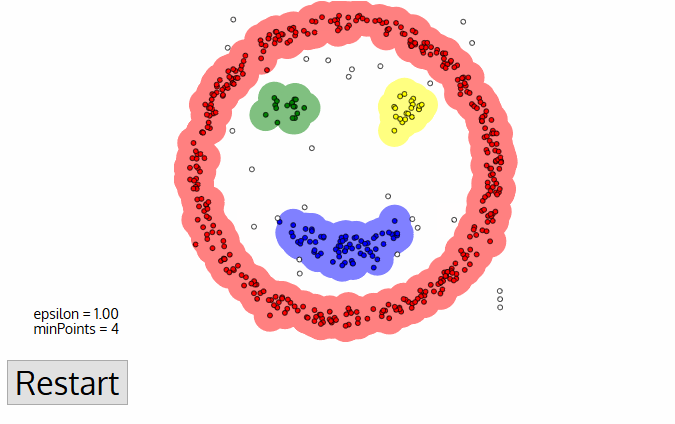
1. DBSCAN alkaa mielivaltainen alkaen tiedot pisteeseen, että ei ole käynyt. Tämän pisteen naapurustoa louhitaan etäisyyden epsilon ε avulla (kaikki ε: n sisällä olevat kohdat ovat lähipisteitä).,
2. Jos on olemassa riittävä määrä pisteitä (mukaan minPoints) tässä naapurustossa niin klusterointi prosessi alkaa ja nykyinen tiedot kohta tulee ensimmäinen kohta uuden klusterin. Muussa tapauksessa piste merkitään meluksi (myöhemmin tästä meluisasta pisteestä saattaa tulla klusterin osa). Kummassakin tapauksessa kyseinen piste on merkitty ”vierailluksi”.
3. tämän uuden klusterin ensimmäisen pisteen kohdalla myös sen ε distance-naapurustossa olevat pisteet tulevat osaksi samaa klusteria., Tämä menettely on tehdä kaikki pistettä ε naapurustossa kuuluvat samaan klusteriin on sitten toistetaan kaikille uusia kohtia, jotka ovat olleet vain lisätä klusterin ryhmä.
4. Tämän prosessin vaiheita 2 ja 3 toistetaan, kunnes kaikki pisteet klusterin määritetään minä.e kaikki pisteet sisällä ε naapurustossa klusteri on käynyt ja merkitty.
5. Kun olemme tehneet nykyisen klusterin, uusi avaamaton vaiheessa haetaan ja käsitellään, mikä löytö edelleen klusterin tai melua. Tämä prosessi toistaa, kunnes kaikki kohdat on merkitty vierailluiksi., Koska lopussa tämän kaikki kohdat on käyty, jokainen piste on merkitty joko kuuluvat ryhmään tai olla melua.

DBSCAN aiheuttaa joitakin suuria etuja verrattuna muihin klusterointi algoritmit. Ensinnäkin, se ei vaadi pe-set määrä klustereita ollenkaan. Se myös tunnistaa poikkeamat ääniksi, toisin kuin Mean-shift, joka yksinkertaisesti heittää ne klusteriin, vaikka datapiste olisi hyvin erilainen. Lisäksi se voi löytää mielivaltaisesti kokoisia ja mielivaltaisesti muotoiltuja klustereita melko hyvin.,

suurin haittapuoli DBSCAN on, että se ei toimi yhtä hyvin kuin muut, kun klusterit ovat eri tiheys. Tämä johtuu siitä, että asetus etäisyys, raja ε ja minPoints tunnistaa naapuruston pistettä vaihtelevat klusterin klusterin, kun tiheys vaihtelee. Tämä haitta esiintyy myös hyvin korkea-ulotteinen tiedot, kun taas etäisyys kynnys ε on haastavaa arvioida.,

Odotus–Maksimointi (EM) Klusterointi Gaussin Seos Mallit (GMM)

Yksi suurimmista haitoista K-means on sen naiivi käytön keskiarvo klusterin keskus. Voimme nähdä, miksi tämä ei ole paras tapa tehdä asioita katsomalla alla olevaa kuvaa. Vasemmalla puolella, se näyttää melko selvää, että ihmisen silmä, joka on kaksi pyöreä klustereita eri säde keskitetty samaan tarkoittaa. K-keinot eivät kestä tätä, koska klustereiden keskiarvot ovat hyvin lähellä toisiaan., K-keinot epäonnistuvat myös tapauksissa, joissa klusterit eivät ole pyöreitä, taas keskiarvon käyttämisen seurauksena klusterikeskuksena.

Gaussian Mixture Models (Gmm) antaa meille enemmän joustavuutta kuin K-means. Gmms oletamme, että datapisteet ovat Gaussin hajautettu; tämä on vähemmän rajoittava oletus kuin sanomalla ne ovat pyöreä käyttämällä keskiarvoa., Näin meillä on kaksi muuttujaa kuvaamaan klustereiden muotoa: keskiarvo ja keskihajonta! Kun otetaan esimerkki kahdesta ulottuvuudesta, tämä tarkoittaa, että klusterit voivat ottaa minkä tahansa elliptisen muodon (koska meillä on standardipoikkeama sekä x-että y-suunnissa). Näin jokainen Gaussin jakauma jaetaan yhteen klusteriin.

löytää parametrit Gaussin kunkin klusterin (esim.g keskiarvo ja keskihajonta), käytämme optimointi algoritmi nimeltään Odotus–Maksimointi (EM)., Katso alla olevaa graafista kuvaa gaussilaisista, jotka on asennettu klustereihin. Sitten voimme edetä prosessin odotuksen-maksimointi klusterointi käyttäen GMM.

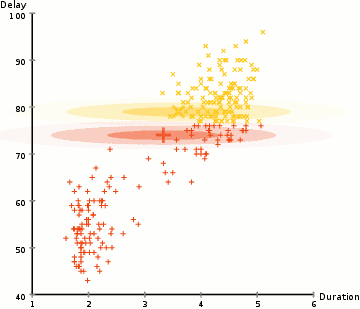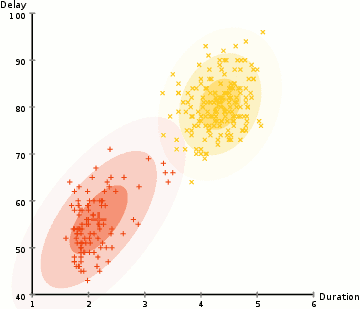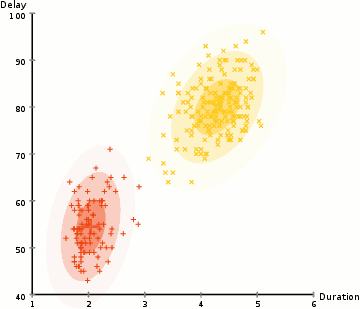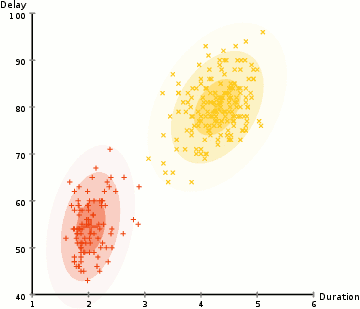
1. Emme aloita valitsemalla useita klustereita (kuten K-means ei) ja satunnaisesti alustetaan Gaussin jakauman parametrit kunkin klusterin., Yksi voi yrittää tarjota hyvä arvaus alkuperäisen parametrit ottamalla Nopeasti tarkastella tietoja liian. Vaikka huomata, kuten voidaan nähdä graafisen edellä, tämä ei ole 100% tarpeen, koska Gaussilaiset alkavat meidän erittäin huono, mutta on nopeasti optimoitu.
2. näiden Gaussin jakaumat kunkin klusterin, laske todennäköisyys, että jokainen datapiste kuuluu tiettyyn klusteriin. Mitä lähempänä piste on Gaussin keskustaa, sitä todennäköisemmin se kuuluu tuohon klusteriin., Tämä pitäisi tehdä intuitiivinen mielessä, koska Gaussin jakauma oletamme, että suurin osa tiedoista sijaitsee lähempänä keskustaa klusterin.
3. näiden todennäköisyyksien perusteella laskemme Gaussin jakaumille uudet parametrit siten, että maksimoimme klustereissa olevien datapisteiden todennäköisyydet. Laskemme nämä uudet parametrit käyttäen painotettua summaa datapisteiden positioista, joissa painot ovat kyseiseen klusteriin kuuluvan datapisteen todennäköisyyksiä., Selittääksemme tämän visuaalisesti voimme tarkastella yllä olevaa graafista, erityisesti keltaista klusteria esimerkkinä. Jakelu alkaa satunnaisesti ensimmäistä iterointia, mutta voimme nähdä, että useimmat keltainen pisteitä oikealle että jakelu. Kun laskemme todennäköisyyksillä painotettua summaa, vaikka keskustan tuntumassa on joitakin kohtia, suurin osa niistä on oikealla. Näin ollen jakauman keskiarvo siirtyy luonnollisesti lähemmäksi niitä pistejoukkoja. Voimme myös nähdä, että suurin osa pisteistä on ”ylhäältä oikealle alas vasemmalle”., Siksi standardipoikkeama muuttuu luodakseen ellipsin, joka on enemmän asennettu näihin pisteisiin, maksimoidakseen todennäköisyyksillä painotetun summan.
4. Vaiheet 2 ja 3 toistetaan iteratiivisesti, kunnes lähentymistä, jossa jakaumat eivät muutu paljon iterointi iterointi.

GMM: n käytössä on 2 keskeistä etua. Ensinnäkin Gmm: t ovat paljon joustavampia kannalta klusterin kovarianssi kuin K-means; koska keskihajonta parametri, klustereita voi ottaa minkä tahansa ellipsin muotoinen, sen sijaan, että rajoitettu piireissä., K-Means on itse asiassa GMM: n erikoistapaus, jossa kunkin klusterin kovarianssi kaikkien ulottuvuuksien suhteen lähestyy 0. Toiseksi, koska GMM: t käyttävät todennäköisyyksiä, niillä voi olla useita klustereita datapistettä kohti. Joten jos datapiste on kahden päällekkäisen klusterin keskellä, voimme yksinkertaisesti määritellä sen luokan sanomalla, että se kuuluu X-prosenttia luokkaan 1 ja Y-prosenttia luokkaan 2. GMM: t tukevat sekajäsenyyttä.

Agglomerative Hierarkkinen Klusterointi

Hierarkkinen klusterointi algoritmit jakaa 2 ryhmään: ylhäältä alas tai alhaalta ylös., Bottom-up-algoritmeja hoitoon jokainen datapiste, koska yhden klusterin aluksi, ja sitten peräkkäin yhdistää (tai agglomeraatti) paria klustereita, kunnes kaikki klusterit on yhdistetty yhdeksi klusteri, joka sisältää kaikki tiedot pistettä. Alhaalta ylöspäin suuntautuvaa hierarkkista klusterointia kutsutaankin hierarkkiseksi agglomeratiiviseksi klusteroinniksi tai HAC: ksi. Tämä klusterien hierarkia on esitetty puuksi (tai dendrogramiksi). Puun juuri on ainutlaatuinen klusteri, joka kokoaa kaikki näytteet, lehdet ovat klustereita, joissa on vain yksi näyte., Tutustu graafisen alla kuva ennen kuin siirrytään algoritmin vaiheet

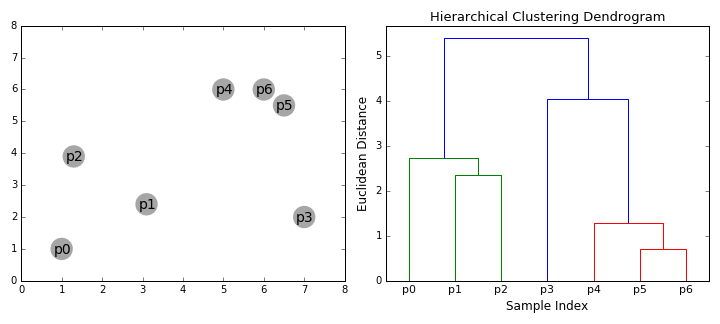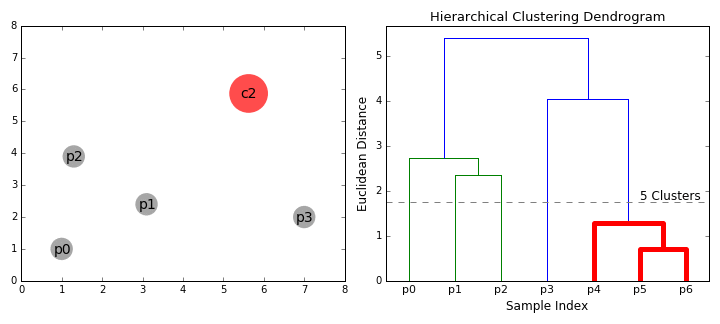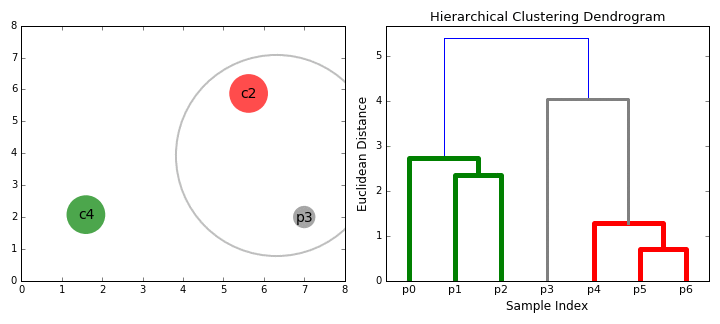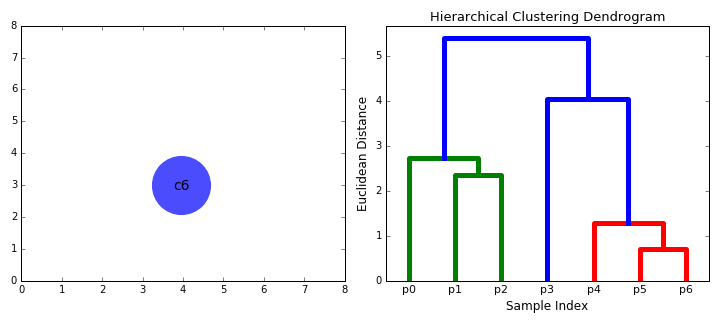
1. aloitamme käsittelemällä jokainen datapiste, koska yhden klusterin minä.e, jos on olemassa X datapisteiden meidän datajoukon sitten meillä on X-klustereita. Valitsemme sitten etäisyysmittarin, joka mittaa kahden klusterin välistä etäisyyttä., Esimerkiksi, käytämme keskimäärin sidonnaisuus, joka määrittelee etäisyyden kahden klustereihin olla keskimääräinen etäisyys tiedot pistettä ensimmäisellä klusterin ja tietoja pistettä toisen klusterin.
2. jokaisella iteraatiolla yhdistämme kaksi klusteria yhdeksi. Yhdistettävät kaksi klusteria valitaan sellaisiksi, joilla on pienin keskimääräinen yhteys. I. e mukaan valitun etäisyyden metrinen, nämä kaksi klustereita on pienin etäisyys toisistaan, ja siksi ovat eniten samanlaisia ja pitäisi yhdistää.
3. Vaihe 2 toistetaan, kunnes päästään puu I: n juurelle.,meillä on vain yksi klusteri, joka sisältää kaikki datapisteet. Näin voimme valita, kuinka monta klusteria haluamme lopulta, yksinkertaisesti valitsemalla milloin lakkaamme yhdistämästä klustereita eli kun lakkaamme rakentamasta puuta!

Hierarkkinen klusterointi ei vaadi meille mahdollisuuden määrittää useita klustereita ja voimme jopa valita, mikä määrä klustereita näyttää parhaiten, koska olemme rakentamassa puu. Lisäksi algoritmi ei ole herkkä valinta etäisyyttä metrijärjestelmän; kaikki ne ovat yleensä toimi yhtä hyvin ottaa huomioon muiden klusterointi algoritmit, valinta etäisyys mittari on kriittinen., Erityisen hyvä käyttää tapauksessa, hierarkkinen klusterointi menetelmiä on, kun taustalla olevat tiedot on hierarkkinen rakenne ja haluat palauttaa hierarkia; muut klusterointi algoritmit voi tehdä tätä. Nämä edut hierarkkinen klusterointi kustannuksella alentaa tehokkuutta, koska se on aikavaativuus O(n3), toisin kuin lineaarinen monimutkaisuus K-means ja GMM.