Varten sähkömagnetismi kaikki mitä sinun tarvitsee tietää on mitä tapahtuu, kun sinulla on + tai – maksuja, mitä tapahtuu, kun he saavat lähellä, ja mitä tapahtuu, kun ne liikkuvat. Juuri noin! Kaikille ei-kvanttisille EMIlle on vain 5 kaavaa, joita tarvitset.,Lorentzin yhtälön kuvata kaikki sähkö, magnetismi, valo, ääni, säteily, itse asiassa useimmat fysiikka:
(1) 
(2) 
(3) 
(4) 
(5) 
Kuinka huono voi aihe olla, jos voit kuvata sitä kaikki vain 5 yhtälöitä, voit ehkä sovittaa ne kaikki takaisin beermat., Nyt kun olet nähnyt johtopäätöksen, voimme mennä alkuun ja lukea koko tarinan yksityiskohtaisesti. Jos et ole tekemässä yliopistokurssia, voit päästä eroon tietämättä tarkalleen, mitä yhtälö tarkoittaa tai tehdä, mutta tämä sivusto selittää ne myöhemmin, ensin palataan perusasioihin.
Perusteet
Maksu tulee 2 tyyppisiä, positiivisia ja negatiivisia, ja se on mitattu Mikrocoulombia (C). Jos sinulla on lataus yksin se lähettää kentän kaikkiin suuntiin. Kenttää latauksesta edustaa e kuten E-lectricityssä., Jos alalle laittaa toisen latauksen, se kokee voiman. Kuten räjähteet hylkivät ja toisin kuin räjähteet houkuttelevat. Isompi maksu vahvempi voima ja kauempana maksut heikompi voima, mitä voit odottaa. Tämä suhde voidaan esittää Mikrocoulombia Lakia;
ja
’s ovat kaksi maksut ja 
on niiden välisen etäisyyden neliöön., Toinen bitti on vain vakio, joka vastaa karkeasti 900000000: ta. (Tämän lain tarkka johtaminen löytyy täältä). Näistä voit nähdä, että voima on vain kentän kertaa mitä veloittaa laittaa, 
. Tämän avulla voit selvittää kentän tai voiman hiukkasten tai atomien välillä tai mitä tahansa varauksella, jos ne eivät liiku. Kun aloitat latauksen, muut asiat tapahtuvat.
Liikkuu
heti Kun maksu alkaa liikkua se tuottaa toinen kenttä., Uusi kenttä on magnetismi ja sitä edustaa B kuten B-magmatismissa?
syy B on yksinkertaisesti se, että se oli toinen asia aakkosellinen lista:
- Sähkömagneettinen vektori potentiaali: A
- Magneettinen induktio: B
- Yhteensä sähkövirta: C
- Sähkö-siirtymä: D
- Sähkömotorinen voima: E
- Mekaaninen voima: F
- Nopeus pisteessä: G
- Magneettinen voimakkuus: H
(Tämä selittää myös sen, missä S tulee niille kiinnostunut).,
Joten nyt hiukkanen tai atom tai mikä on 2 kenttää tulossa ulos. Koko yhtälö kuvaamaan, miten molemmat kentät toimivat hiukkanen on
joka tunnetaan nimellä Lorentzin voima. 
symboli ei tarkoita, kerto -, tässä yhteydessä se tarkoittaa, Cross-Tuote. Se on pohjimmiltaan lyhyt tapa kirjoittaa ”
kertaa 
kertaa kulman sini välillä”., Tämä on koska kenttä työntää 90° kumpi suuntaan sen osoittaa JA jossa koskaan suuntaan olet menossa. Nyt jos olet tehnyt NIITÄ aiemmin A-tasolla, voit unohtaa suuntiin ja kulmat ja vain kirjoittaa,
Jos me laajentaa ulos edellä ilmaisun meillä on
Mutta voimme jo kuvata yksi näistä bittiä, 
on vain Mikrocoulombia Laki., Myös at-tasolla tai sen alapuolella, tilanne on luultavasti yksinkertaistettu, joten sinun tarvitsee vain harkita 
ja kentät erikseen., Joten sinulla todennäköisesti tarvitsee vain käyttää yhtä seuraavista kaksi kaavat,
Ilmeisesti 
voima, ja ei vastaa, ja ovat kaksi kenttää aiemmin kuvattu ja on nopeus, liikkuvat maksu., Sähkökentän mitataan SI-yksiköt Newtonia per coulombi (
) tai vastaavasti, volttia per metri (
). Magneettikenttä on SI-yksiköt Teslaa (T), joka vastaa Webers neliömetriä kohti (
) tai voltin sekuntia per neliömetri (
)
Piirit
Nyt en ole suuri fani piirejä, ei koskaan ollut, nyt toivottavasti tulee olla ammatillinen tarpeeksi, että minun vastenmielisyyden niitä ei törmännyt tässä jaksossa, mutta jos se ei pyydän etukäteen anteeksi., Jos todella alkaa kamppailla vihani en voi kutsua toinen kirjoittaja,
A-piirejä on pohjimmiltaan vain joukko liikkuvia maksut satunnaista esinettä tai laitetta niin, että se vaikuttaa virtaus. Nyt kun sanon elektronit liikkuvat ympäri useimmat ihmiset ajattelevat, että niiden ylinopeutta noin lähellä valonnopeutta, mutta tämä on väärin. Varsinaiset elektronit liikkuvat erittäin hitaasti, juuri aalto kulkee nopeasti. Kuten edellä on esitetty, kuten räjähteet hylkivät, joten laita yksi elektroni toisen viereen ja ne liikkuvat toisistaan., Nykyinen lanka, voit periaatteessa on putki elektroneja, ja olet lisäämällä yksi yksi päättyy, tämä aiheuttaa seuraavan electron liikkua alaspäin, joka puolestaan työntää seuraava yksi ja niin edelleen. Meksikolainen aalto liikkuu nopeasti, mutta itse elektronit liikkuvat vain hitaasti.
Piirit sisältävät yleensä kaikenlaisia erilaisia esineitä ja laitteita, riippuen siitä, mitä he ovat, ja riippuen siitä, kuinka olet asettanut ne kaikki ylös piiri riippuu siitä, miten voit tehdä kaikki laskelmat.
mikä on kumpi?,
Jos olet määrittänyt kaikki osa suljetun silmukan, kuten niin
sitten sanomme, että kaikki komponentit ovat Sarjassa. Jos olet määrittänyt ne aluevaltaus polkuja, kuten niin
sitten sanomme, että osat ovat Rinnakkain. Voit myös tehdä piirejä, jotka ovat sekoitus sarja-ja rinnakkais-osiossa, kuten niin
Ampeeria, Volttia ja Ohmia (Oh my!,)
kutsumme liikkuvat maksut Nykyinen, ja sitä mitataan SI-yksikkö Ampeeri (A). Vahvistimet ovat määrää vastaava maksu kulunut tietty aika, niin 2 mikrocoulombia 6 sekuntia vastaa 0,3 A. Tämä, kuten useimmat asiat fysiikassa voidaan ilmaista kiva kaava, voit oppia
Toinen tärkeä ajatus piirit on Jännite tai Potentiaali-Ero. Voltit ovat periaatteessa ero sähköpotentiaalissa kahdessa eri pisteessä., Sähköinen potentiaali välillä 2 pistettä annetaan.
jossa 
on etäisyys 
ja 
. Se on käytännössä kenttä kertaa etäisyys.
Toinen tärkeä idea, kun se tulee piirit on vastus. Vastus on pohjimmiltaan mittari siitä, kuinka paljon vastus vastustaa sähkövirtaa., Lähes kaikki esineet tai laitteet piiri koska vastuksen ja laskea koko vastus piiri voit käyttää yhtä tai useampaa näistä säännöistä.
Yksi tärkeimmistä ja perustavaa yhtälöt piirit on Ohmin laki, ja se koskee virta, jännite ja vastus.
The Deep End
Tämä on se. Klassinen EM ei mene tätä syvemmälle., Nämä 4 ovat Perusyhtälö kaikille aloille EM. Ne voivat kestää hieman saada pään ympäri, mutta kun teet sen pitäisi kaikki järkevää, tavallaan.,
Jos et tiedä integraatio ja eriyttäminen ehdotan pään yli Integrointi osassa tai Eriyttäminen osiossa yritän selittää sen täällä, mutta olen lähinnä keskittyen fysiikan.
Gaussin laki
Ok sitten ensin on Gaussin laki.,
Tämä sanoo, että olennainen sähkökentän, kautta suljettu alue 
on yhtä kuin koko maksu sisällä alue, 
jaettu 
. on vakio, kutsutaan Permittiivisyys Vapaata Tilaa ja näkyy ympäri fysiikka yhdessä 
jossa on Läpäisevyyttä Vapaata Tilaa., Mitä tämä yhtälö tarkoittaa, voit ottaa minkä TAHANSA suljetun pinnan ja löytää kentän läpi, jos voit tehdä matematiikka. Yleensä et voi. kuitenkin on olemassa useita tapauksia, kun se on mukava ja helppo. Tapaukset, joissa kenttä tulee suoraan pinnan läpi tasaisesti., Tapaukset ovat
- Pallomainen pinta noin piste tai pallo
- Lieriömäinen pinta noin ääretön lanka
- Säännöllinen pinnan yli osa ääretön kone
myönnän, nämä kuulostaa epämääräinen ja abstrakti, joten minun on osoitettava tuki-kaavio.
Nämä ovat Gaussin pinnat., Näillä pinnoilla yrität vain helpottaa elämää. Vain varmista, että pinta on aina sama etäisyys maksu lähde ja että kenttä on aina menossa läpi 90 astetta. Voit sitten selvittää integraalin silmät kiinni sen helppoa. Gaussin lain vasen puoli muuttuu e kertaa valitsemasi muodon pinnaksi.
- Pallomainen pinta tulee
, jossa 
on pallon säde., - Lieriön pinnasta tulee
, jossa ja ovat pituus ja säde sylinterin. - Säännöllinen pinta tulee
, jossa 
on-Alue ylä-ja alapuolella ääretön pinta (tarvitset kertoimella 2, kun kenttä menee edellä ja pinnan alle 90 astetta).,
So Gauss’ law for a sphere becomes
Which was introduces earlier as Coulombs Law, now you know where it came from., Gauss’ Laki ääretön line maksutta on vain
Nyt tässä jotain uutta on otettu käyttöön, 
. Jos sinulla on ääretön line veloituksetta sitten koko maksu on ääretön ja ei ole mitään keinoa tietää, kuinka paljon, että ääretön maksutta olisit sisällä gaussin pinta., Se on jossa tulee, sen arvo vastaa yksikön pituutta kohden, joten jos =4
ja sinulla on 5 metriä, sitten maksu on vain 20C. Se on kaikki ei, vain arvo-veloituksetta.
ääretön pinta gauss’ laki tulee
jälleen uusi symboli on lisätty, mutta sen aivan kuten ennen., 
on vain maksu pinta-alayksikköä kohti, joten jos =5Cm
ja sinulla on 100m
alue koko maksu on 500C.
Ladattu Rengas
Lets sanoa olet saanut ladattu rengas ja sinun täytyy tietää, kenttä, jotka on valmistettu siitä. Jälleen kerran käytämme yhtä fysiikan tärkeimmistä työkaluista, mikä helpottaa asioita. Ensinnäkin katsomme vain, kenttä-akselilla rengas, muuten asiat vain saada liian monimutkainen, ja se ei ole vaivan arvoista., Otetaan pieni osa kehästä ja sanotaan, että se on pallo. Tämä ei pidä paikkaansa, mutta mitä pienemmästä osiosta tehdään, sitä enemmän se muistuttaa pistelatausta. Joten sinulla on jotain tällaista,
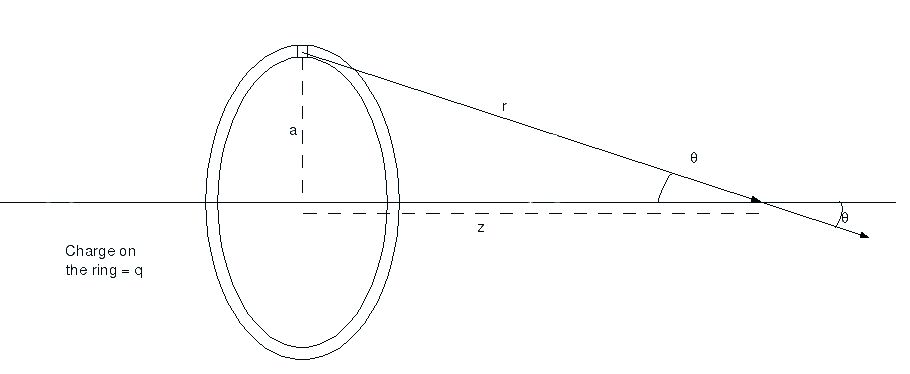
haluat löytää kentän pisteessä 
akselilla rengas koko maksu ja säde . Pieni neliöosa yläosassa, se on vähän, että oletat on ladattu pallo., Nyt emme tiedä, kuinka paljon virtaa on, että pieni osa, koska voit tehdä sen minkä kokoisia tahansa haluat, niin me vain soittaa maksutta 
, pieni määrä . Joten meillä on nyt
Nyt jos ajattelee sitä, jokainen vähän renkaan yläpuolella akseli työntää alas on yhtä suuri hieman alle akseli nousevat. Sama pätee myös vasempaan ja oikeaan sekä kaikkiin muihin kehän osiin., Kaikki voima kehästä toimii siis vain akselin suuntaisesti. Jotta voimme selvittää vain tämän osan, meidän täytyy käyttää trigiä. Meidän täytyy kertaa kentän 
saada aksiaalinen komponentti.,
As you may or may not know can also be described (using SOH CAH TOA) by the following relationship for our situation
As is the adjacent side and is the hypotenuse., Niin, nyt olemme
emme Kuitenkaan voi tietää, mitä on. Tiedämme levyn säde, , ja etäisyys olemme levyltä, .,on
Nyt haluamme päästä eroon, että , joten me yhdistää
Nyt tiedämme kaavio alussa, että koko maksu levyllä on , joten jos lisäämme kaikki vähän bittiä koko pitäisi olla , niin integraali on vain .,
Joten sinulla on se, kentän ladattu levy. Tarvitset vain kentän pisteestä ja jonkin verran trig-tietoa ja voit selvittää sen. Olisin voinut antaa sinulle lopullisen ratkaisun, mutta näin näet, mistä se tuli, ja jos unohdat sen, voit ehkä selvittää sen ensimmäisistä periaatteista, kuten edellä.,
Gauss’ Laki Magnetismi
Tämä on mukava ja helppo, mutta on joitakin suuria vaikutuksia. Gauss’ Laki Magnetismi on
Sen kuin tavallinen gauss’ laki, että se kuvaa kenttä, tällä kertaa sen magneettikentän, . Sen mukaan B: n integraali suljetun pinnan, 
on nolla. Mitään. Jokaisella pinnalta lähtevällä kenttäviivalla on vastaava, joka menee sisään. Yleistä kenttää ei ole., Tämä tarkoittaa, että sen on mahdotonta saada lähteitä magneettikentän. Ottaa huomioon, että elektronit ja protonit ovat alkuperä-kenttä, josta kenttä linjat poikkeavat tai lähentyvät, ei ole magneettinen analoginen. Magneettikentän linjat ovat aina suljettuja silmukoita, ei aloitusta, ei loppua. Tämä ei tietenkään ole estänyt ihmisiä valmistelusta jos löydämme magneettisen monopolin.
Tämä yhtälö voi tuntua kiva, ja se on, mutta se on täysin hyödytön yksinään., Yleensä 0-tulos fysiikassa on melko tärkeää, se tarkoittaa, että jotain erityistä tapahtuu, täällä se osoittaa magneettisia monopoleja ei ole olemassa.
Faradayta, Laki
Nyt asiat ovat yhä monimutkaisempia, tässä meillä on Faradayta, laki,
saatan sinut läpi jokaisen hieman näyttää, mitä se todella tarkoittaa. Ensin meillä on vasen puoli, joka on helppo. Sen aivan kuten Gaussin lain vain integraali on yli eri asia., Sen sijaan löytää yhteensä kentän läpi pinnan, olemme nyt löytää yhteensä kentän ympäri suljetun silmukan 
. Siinä kaikki, mikä on erilaista vasemman käden puolella, ei enää pintoja, vain suljetut silmukat. Oikealle puolelle. Ensinnäkin meillä on miinus, huomata monimutkainen siitä. Miksi sen siellä selitetään myöhemmin. Seuraavaksi meillä on toinen integraali, ja tämä näyttää kamalalta. 
Symboli tarkoittaa käytännössä pientä muutosta., Niin 
muuttuu ja 
muuttuu 
, jossa on aika. Koko 
on muutosnopeus , sen kuinka paljon muuttuu () tiettynä aikana (). Ja se integroidaan alueelle ., on alue sisällä suljetun silmukan , jos et tehdä joitakin satunnaisia koukeroinen asia, varmista, että linja ei rajat itse ja että se liittyy itse niin pituus noin linja on teidän ja alueen sisällä linja on teidän . Yksinkertainen kyllä? Joten yhteensä noin silmukka on yhtä suuri kuin miinus muuttuvassa silmukan läpi.
Mitä tapahtuu, jos ei ole ?, No ei , niin on nolla, mikä tekee olennainen 0, niin n . Mitä tapahtuu, jos sinulla on vakio ? Well again on 0. Niin on nolla, mikä tekee olennainen 0, niin taas ei . Voit vain aiheuttamaan kentän muuttaminen kenttä.,
merkitystä miinus tulee siitä, että kentät luo kentät ja kentät luo kentät (Kuten kuvassa Faradayn ja Ampere Lakeja). Jos miinusta ei olisi, niin kentät vain jatkaisivat rakentamista ja rakentamista antaen lopulta ääretöntä energiaa, ja se ei ole sallittua!
Ampère-Maxwellin Laki
viime Maxwellin Yhtälöt on Ampere-Maxwellin laki., Aivan kuten kaksi ensimmäistä lakia olivat samanlaisia, niin ovat kaksi viimeistä, on kaava heille tässä järjestyksessä, joka voi tehdä niistä helpompi muistaa. yli ala, yli ala, noin silmukka, ja nyt vihdoin noin silmukka. Yhtälö on
Vasemmalla puolella, helppo, integraali B noin suljetun silmukan. Oikea käsi, ei niin helppoa., First lets ignore the 
bit, I ’ ll come back to that. Muut kuin 
, sen hyvin samanlainen Faradayta laki. Sinulla on toinen muuttuvassa kentässä integroitu yli alue, mutta tällä kertaa sen . Tällä kertaa tosin sijaan kertomalla miinus 1, olet kertomalla 
. Jälleen kerran nämä ovat kaksi hyvin tärkeää arvoa fysiikassa, yksin ja yhdessä. He ovat EM: n ytimessä., Joten magneettikentän ympärillä silmukka on vain yhtä muuttuvat E-kentän läpi se kertaa , mutta sitten sinun täytyy lisätä hieman. Tämä on bitti. Tämä on vain nykyinen kiertänyt silmukka kertaa tämä on, koska, kuten sanottu Juttuja Liikkuu, jos sinulla on siirtymässä maksu eli nykyinen, niin saat magneettisen kentän. Joten sinun täytyy lisätä kaksi bittiä yhteen. Valmista tuli.,
Toinen Muoto Deep End
sekä kirjoittaa Maxwellin yhtälöt edellä, mikä on nimeltään kiinteä muoto, voit myös kirjoittaa niitä differentiaali-muodossa, kuten niin
Vielä Toinen Muoto Deep End
Kirjoittaa Maxwellin yhtälöt vuonna yksi ennen kahta on todella yksinkertaistamista., Sekä kiinteä muoto ja ero muodossa on vektori yhtälöt ja ne säästävät sinua ottaa kirjoittaa koko 8 Maxwellin yhtälöt ja kentät kaikki kolme ulottuvuutta.,div id=”a2ea6619e6″> 
Well iot turns out you can also compactify the four vector Maxwell equations into two tensor equations like so
Here 
is a vector with four components, sometimes called the 4-current, and 
is a 4×4 matrix called the electromagnetic tensor., Ne määritellään
(6) 
(7) 
jossa 
on valon nopeus. 
ja 
vain kertoa, missä vektori tai matriisi näyttää, mutta erehdyttävästi jostain alkaa 0, niin 
ja 
(ei pidä sekoittaa 
kuutioitu). Sama , niin 
ja 