Icosahedron (Suomi)

säännöllinen ikosaedri on yksi viidestä Platoninen kiintoaineita. Se on kupera säännöllinen monitahokas koostuu kahdestakymmenestä kolmionmuotoinen kasvot, jossa viisi kokousta kussakin kahdestatoista vertices. Siinä on 30 reunaa ja 12 kärkeä. Sen dual monitahokas on dodekaedri.,

Mitat

Jos reunan pituus säännöllinen ikosaedri on , säde sidotun alalla (yksi, joka koskettaa icosahedron kaikki vertices)

ja säde kaiverrettu pallo (tangentti kussakin icosahedron on kasvot) on

kun midradius, joka koskettaa keskellä jokainen reuna, on,

jossa 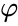(kutsutaan myös ) on kultainen suhde.,

– Ala ja tilavuus

pinta-ala ja tilavuus säännöllinen ikosaedri reunan pituus ovat:

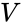
Suorakulmaiset koordinaatit

seuraavat Suorakulmaiset koordinaatit määrittää vertices, ikosaedri edge-pituus 2, keskitetty alkuperä:

jossa on kultainen suhde (myös kirjoitettu τ)., Huomaa, että nämä vertices muodostavat viisi sarjaa kolme keskenään keskitetty, toisiaan ortogonaalinen kultainen suorakulmioita.

12 reunat säännöllinen octahedron voi olla osioitu kultainen suhde niin, että tuloksena vertices määritellä säännöllinen ikosaedri. Tämä on tehty siten, että ensin asettamalla vektorit pitkin octahedron on reunat siten, että jokainen kasvot on rajoittuu ajan, sitten vastaavasti osiointi kunkin reunan kultainen keskitie pitkin suuntaan sen vektori., Viisi octahedra määritellään tiettynä icosahedron muodossa säännöllinen polyhedral yhdiste, samoin kaksi icosahedra, joka voidaan määritellä näin mistä tahansa octahedron.

Rakentaminen järjestelmä equiangular rivit

seuraavat rakentamisen icoshaedron välttää tylsiä laskelmat määrä-kenttään tarpeen enemmän peruskoulun lähestymistapoja.

Olemassaolon icosahedron merkitsee olemassaolon kuusi equiangular rivit ., Itse asiassa, intersecting tällainen järjestelmä equiangular linjat Euklidinen pallo keskitetty niiden yhteinen risteys tuottaa kaksitoista vertices säännöllisen ikosaedri kuten voidaan helposti tarkistaa. Kääntäen, oletetaan, että on olemassa säännöllinen ikosaedri, linjat määritelty sen kuusi paria vastapäätä kärkipisteet muodostavat equiangular järjestelmä.

jotta rakentaa tällaisen equiangular järjestelmän, me aloittaa matriisi

neliön koko ., (Muistisääntö: matrix koodaa kulmat, akuutti positiivinen merkintä, tylppä muuten, välillä viisi syklisesti peräkkäisen vertices vieressä ensimmäinen vertex ja ikosaedri keskitetty alkuperä.)

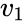
suoraviivainen laskenta saannot . Tämä merkitsee sitä, että on ominaisarvot , sekä moninaisuus 3 jälkeen on symmetrinen ja jäljittää 0., Matrix indusoi thusan Euklidinen rakenne osamäärä tilaa , joka on isomorphic koska kernel ja ulottuvuus on 3. Kuvan alla projektio kuuden koordinaattiakselien vuonna lomakkeet siten asystem kuusi equiangular rivit leikkaavat pareittain yhteinen akuutti kulma ., Ortogonaalinen projektio päälle -eigenspace on saadaan näin kaksitoista vertices, ikosaedri.

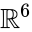
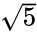
toinen yksinkertainen rakenne icosahedron käyttää edustus teoria vuorotellen ryhmän puolesta toimii suoraan isometries on icosahedron.

tähtikuviot

kirjassa määriteltyjen erityissääntöjen mukaan tavalliselle ikosaedrille tunnistettiin 59 tähtikuviota. Ensimmäinen muoto on ikosaedri itse., Yksi on tavallinen Kepler-Poinsot kiinteä. Kolme on säännöllisiä monitahokkaita.

21 59 stellations

kasvot icosahedron laajennettu ulospäin, koska koneet leikkaavat, jossa määritellään alueiden tilaa, kuten on esitetty tämän stellation kaavio risteyksiä yhdessä tasossa.,

Geometric relations

Icosahedron as a snub tetrahedron.,

Icosahedron as an alternated truncated octahedron.

There are distortions of the icosahedron that, while no longer regular, are nevertheless vertex-uniform., Nämä ovat invariant nojalla sama kierrosta kuin tetraedrin, ja ovat hieman samanlainen tölväistä kuutio ja snub dodekaedri, mukaan lukien joitakin muotoja, jotka ovat kiraalinen ja jotkut Th-symmetria, eli on eri tasoissa symmetria päässä tetraedrin. Icosahedron on suuri määrä stellations, mukaan lukien yksi Kepler-Poinsot polyhedra ja joitakin säännöllinen yhdisteitä, joita voitaisiin keskustella täällä.

icosahedron on ainutlaatuinen Platoninen kiintoaineita jolla diedrikulma ei pienempi kuin 120°. Sen dihedraalinen kulma on noin 138,19°.,ss on vähintään 120° ja ei voi käyttää kasvot, kupera säännöllinen monitahokas, koska tällainen rakenne ei täytä vaatimusta, että vähintään kolme kohtaa kokoontuu vertex ja jättää positiivisen vika taitto kolmiulotteisesti, icosahedra ei voi käyttää, koska solujen kupera säännöllisesti polychoron koska, vastaavasti vähintään kolme solua on tavata reuna ja jättää positiivisen vika taitto neljä ulottuvuutta (yleensä kupera polytope vuonna mitat, vähintään kolme puolia on tavata huipussaan ja jättää positiivisen vika taitto n-tila)., Kuitenkin, kun yhdistetään sopiva soluja, joilla on pienempi dihedral näkökulmista, icosahedra voidaan käyttää solujen semi-säännöllinen polychora (esimerkiksi tölväistä 24-solu), aivan kuten laput voidaan käyttää kasvot semi-säännöllisesti polyhedra (esimerkiksi typistetty ikosaedri). Lopuksi, ei-kupera polytopes eivät ole yhtä tiukat vaatimukset kuin kupera polytopes, ja icosahedra ovat todellakin solujen ikosahedraalinen 120-solu, yksi kymmenestä ei-kupera säännöllisesti polychora.

ikosaedria voidaan kutsua myös gyroelongatuksi viisikulmaiseksi bipyramidiksi., Se voidaan jakaa gyroelongated viisikulmainen pyramidi ja viisikulmainen pyramidi tai viisikulmainen antiprism ja kaksi yhtä suuri viisikulmainen pyramidit.

icosahedron voidaan kutsua myös väheksyntää tetraedrin, kuten snubification säännöllisen tetraedrin antaa säännöllinen ikosaedri., Vaihtoehtoisesti voit käyttää nimikkeistö tölväistä polyhedra, joka viittaa tölväistä kuutio väheksymistä cuboctahedron (cuboctahedron = korjattu kuutio) ja väheksyntää dodekaedri väheksymistä icosidodecaedri (icosidodecaedri = korjattu dodekaedri), yksi voi soittaa icosahedron tölväistä octahedron (octahedron = korjattu tetrahedron).

korjattu ikosaedri muodostaa ikosidodekaedrin.

Icosahedron vs dodekaedri

Kun ikosaedri on kaiverrettu pallo, se vie vähemmän pallon tilavuus (60.54%) kuin dodekaedri kirjoitettu vuonna sama pallo (66.49%).,

myös, koska nämä ovat kaksinkamppailuja, on mahdollista muuttaa toinen(KS.alla).,

Icosahedron

Truncated icosahedron

Icosidodecahedron

Truncated dodecahedron

Dodecahedron

Uses and natural forms

In 1904, Ernst Haeckel described a number of species of Radiolaria, including Circogonia icosahedra, whose skeleton is shaped like a regular icosahedron. A copy of Haeckel’s illustration for this radiolarian appears in the article on regular polyhedra.

	joissakin roolipelit, kaksikymmentä puolinen die (lyhyesti, d20) käytetään määritettäessä menestys tai epäonnistuminen toiminnan. Tämä kuolee tavallisen ikosaedrin muodossa. Se voi olla numeroitu ”0” – ”9” kahdesti (missä muodossa se yleensä toimii kymmenen puolinen die, tai d10), mutta useimmat modernit versiot on merkitty ”1” ”20”. Katso D20-järjestelmä.,

ikosaedri on kolmiulotteinen peli aluksella Icosagame, joka tunnettiin aiemmin nimellä Ico Crystal Peli.

ikosaedri on käytetty lautapeli Scattergories valita kirjaimen. Kuusi vähän käytettyä kirjainta, kuten X, Q ja Z, on jätetty pois.

Sisällä Magic-8-Pallo, erilaisia vastauksia kyllä-ei kysymyksiä on painettu säännöllinen ikosaedri.

funktionaalisessa muodossa esitetty ikosaedri näkyy Sol de la Florin valosävyssä., Päällekkäisten kappaleiden muodostama ruusuke muistuttaa frangipanin kukkaa.

Jos jokainen reuna ikosaedri on korvattu yhden ohmin vastus, vastus välillä vastapäätä vertices on 0.5 ohmia, ja että vierekkäisten vertices 11/30 ohmia.

ikosaedrin symmetriaryhmä on isomorfinen vuorottelevan ryhmän kanssa viidellä kirjaimella. Tämä nonabelilainen yksinkertainen ryhmä on symmetrisen ryhmän ainoa nontriviaalinen normaali alaryhmä viidellä kirjaimella., Koska Galois ryhmän yleinen quintic yhtälö on isomorphic on symmetrinen ryhmä viisi kirjainta, ja se, että ikosahedraalinen ryhmä on yksinkertainen ja nonabelian tarkoittaa, että quintic yhtälöt, ei tarvitse olla ratkaisu radikaalit. Todiste Abel-Ruffini lause käyttää tätä yksinkertainen tosiasia, ja Felix Klein kirjoitti kirjan, joka teki käytön teoria ikosahedraalinen symmetries perustuvat analyyttinen ratkaisu yleiseen quintic yhtälö.,

Katso myös

Malli:Wiktionarypar

• Typistetty ikosaedri
• Säännöllinen monitahokas
• Geodeettista ristikot käyttää iteratiivisesti puolitetaan icosahedron tuottaa ristikot pallolla
• Jessen on icosahedron

Malli:Wikisource1911Enc

Malli:Commonscat

• Weisstein, Eric W., ”Icosahedron” alkaen MathWorld.
• Paperi malleja icosahedron
• Yhtenäinen Polyhedra
• K. J. M., MacLean, Geometrinen Analyysi Viisi Platonin Kiintoaineita ja Muita Semi-Säännöllisesti Polyhedra
• Vuorovaikutteinen Icosahedron malli – toimii suoraan web-selaimella
• virtuaalitodellisuus Polyhedra Tietosanakirja Polyhedra
• Tulane.,edu on keskustelua, super rakenne ja icosahedron
• Paperi Malleja Polyhedra Paljon linkkejä
• Origami Polyhedra – Mallit on tehty Modulaarinen Origami
• video ikosahedraalinen peili on veistos

Malli:Polyhedra

az:Ikosaedrca:Icosàedrecs:Dvacetistěnda:Ikosaederet:Ikosaeedereo:Dudekedrofa:بیستوجهیit:Icosaedrohe:איקוסהדרוןlv:Ikosaedrshu:Ikozaédernl:Icosaëderno:Ikosaederpl:Dwudziestościan foremnypt:Icosaedrosimple:Icosahedronsq:Ikosaedri en rregulltsr:Икосаедарsv:Ikosaederta:puhkesi முக்கோணகம்th:ทรงยี่สิบหน้าuk:Ікосаедр.