Jakaumat
keskeinen kysymys ytimessä ongelmia Diracin delta ja vastaavat
matemaattinen esineitä, on ongelma differentiability. Kuten Dirac mainittu lainaus edellä, et voi todella ajaa vaikeuksiin, jos et käytä hänen δ-funktio symbolisena sääntö, miten se toimii muita toimintoja; kuitenkin, hän etenee erottaa δ hänen laskelmat, ja tämä on, jos ongelmia alkaa., Miten voi tietää etukäteen ”milloin nämä toiminnot ovat sallittuja”, kun ei ole edes tarkkaa määritelmää esineistä tai mitä niiden erottaminen merkitsisi? Näemme, miten nämä kysymykset johtavat uusien ja täsmällisesti määriteltyjen matemaattisten objektien johtamiseen.
Funktionaalit
mieti, miten funktion derivaatta (tai antiderivatiivista) yleensä määritetään. Normaaleissa olosuhteissa, kun ”klassisen” toiminnot, sinulla on hyvin määritelty sääntö, joka kuvaa, kuinka toiminta maps yksi joukko reaalilukuja toiseen joukko, sanotaan f : ℝ →ℝ., Kun otetaan huomioon tämä ja määritelmät kiinteä tai johdannainen, voi sitten selvästi tutkia arvoja, joita nämä toimijat tuotto, kun sitä sovelletaan toiminto. Δ: n tapauksessa meillä ei ole toimivaa määritelmää edetä näillä linjoilla. Sen sijaan käytännössä δ määritellään näkyvimmin sen mukaan, miten se toimii muilla tarkoin määritellyillä funktioilla (kuten kohdassa (3)). Tämä on keskeinen oivallus, joka johtaa nykyaikaiseen jakaumateoriaan. On käynyt ilmi, että oikea tapa matemaattisesti hoitoon δ, ja suuren luokan vastaavia esineitä, on lopettaa yrittää määritellä ne toiminnot lainkaan., Tämä ajattelutapa on hyvin kuvattu Jean Dieudonne hänen tarkastelu (ks.):
– yksi alkaa perheen hyvin ”tavallinen” toiminnot (yleensä
kunnioittaen differential properties), jotka täyttävät tietyt (yleensä
kiinteä) suhteita, tai jossa tietyt toiminnot ovat mahdollisia; ja
sitten yksi tajuaa, että lähtökohtaisesti suurempi perheen toimintoja täyttää
sama suhteita, tai voidaan suorittaa vastaavia operaatioita. Monia
kysymyksiä sitten voidaan luonnollisesti kysyä: onko tämä uusi perhe todella
erilainen kuin ensimmäinen?, Jos on, mitkä ovat
kahden perheen väliset suhteet, ja voiko uudesta antaa tarkan kuvauksen?
Se on vain viimeinen vaihe ”esihistoria”, että mitä voi olla
kutsutaan vallankumouksellinen näkökulmasta tulee esiin, ajatus, että
”uusi perhe” saattaa koostua esineet, muut kuin toimintoja.
muita esineitä viittasi ovat functionals. Funktionaalin
voi ajatella funktiona., Kun toiminto on ainutlaatuinen kartoitus yhdet
numerot toiseen, toiminnallinen F voidaan määritellä kuvaus F : C →ℝ,
, missä C on jokin joukko toimintoja. Toisin sanoen funktionaalinen kartta toimii reaalisille
– numeroille., Yksinkertainen esimerkki toiminnallisen tämä tyyppi on määrätty integraali:

joka selvästi ottaa funktio f jotkut joukko sopivasti integrable toiminnot ja kartat se todellinen määrä, arvo, kiinteä, tai alle jäävä pinta-ala f(x) a ja b välillä. Tämä on vain yksi esimerkki., Yksi voi kuvitella ääretön määrä functionals, ja sarjaa functionals; voisi jopa jatkaa yleistää, ja määritellä kuvaukset alkaen sarjaa functionals todellinen määrä. Se ei ole täällä eikä siellä. Tärkeää on, että funktionaalista käsitettä voidaan käyttää jakaumien määrittelyssä.
testitoimintojen joukko
tavoitteen saavuttamiseksi tarvitaan vielä yksi määritelmä. Tämä tarkoittaa sellaisten funktioiden joukon C määrittelyä,joista jakaumat kartoittavat funktioita reaalilukuihin., Funktiot kerätään usein sarjoiksi, joissa määritellään niiden jatkuvuus, differentiabiliteetti ja johdannaisten jatkuvuus. Me sanomme, että funktio f on asetettu C⁰ (kirjoittaa f ∈ C⁰), jos se on jatkuva koko reaaliakselilla siinä mielessä, että raja-kaikissa kohdissa on sama, kun otetaan vasemmalle tai oikealle; se ei ole välttämättä derivoituva. Sanomme, että f ∈ C1 jos sen derivaatta on olemassa ja on jatkuva, eli f ’ ∈ C⁰. Esimerkiksi funktio g(x) = |x| on jatkuva, mutta ei derivoituva kohdassa x= 0; g on C⁰ mutta ei C1., Voimme yleistää ja sanoa, että Cⁿ on joukko toimintoja, jotka ovat jatkuvien toimintojen ensimmäisen n johdannaiset, missä n on kokonaisluku.
kun n kasvaa suuremmaksi, joukoista tulee tavallaan ”pienempiä;” funktioita löytyy aina (äärettömän monta!) jotka ovat cⁿ, mutta eivät Cⁿ ⁺ 1. Nämä ”jatkuvuusavaruudet” muodostavat siis joukon sisäkkäisiä osajoukkoja, kuten alla on kuvattu.

alaosassa tämä loputon jono sarjaa toimintoja, löydämme set
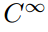
mikä on tietenkin asetettu kaikki toiminnot, joilla on äärettömän monia jatkuva johdannaiset. Monet tunnetut ja ystävälliset funktiot kuuluvat tähän jälkimmäiseen luokkaan(esimerkiksi sin(x); cos (x); eˣ; kaikki polynomit)., Nämä toiminnot ovat nimeltään ”pehmeä” tai ”hyvin käyttäytyviä”, koska yksi voi suorittaa toiminnan eriyttäminen niitä niin monta kertaa kuin tahtoo ilman hoitoa. Mutta kun tämä sarja on varmasti äärettömän monta jäsentä, ne ovat harvinaisia siinä mielessä, että useimmat toiminnot eivät ole niin hyvin käyttäytyviä.
jakaumien määrittelyyn soveltuva joukko on tätäkin pienempi
. Se edellyttää lisäkriteeriä: että toiminnoilla on kompakti tuki. Tämä tekninen termi tarkoittaa yksinkertaisesti sitä, että funktiolla on nonzero-arvot äärellisessä domainissa, ja se on tasaisen nolla tämän ulkopuolella., Meidän on siis käytettävä merkintätapa
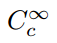
kuvaamaan joukon äärettömän jatkuvasti derivoituva toimintoja kompakti tukea, ja soittaa tällaisia toimintoja, testata toimintoja. Jotta voidaan määritellä luokka funktionals käyttämällä tätä joukkoa verkkotunnuksena, meidän pitäisi olla varmoja, että on olemassa todella jäseniä tämän joukon., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

Määrittely
tästä eteenpäin määritelmä jakelu on yksinkertaista. Jakelu on lineaarinen toiminnallinen
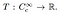
tämä on, se on kartoitus joukko testi-toiminnot todellinen määrä. Analoginen, miten tietty toiminto toimii input numero ja tuottaa erityisiä jakaumat määritellään, miten ne muuttavat testi toiminnot osaksi numerot., Testifunktion φ jakauma voidaan kirjoittaa muodossa T (φ) tai yleisesti muodossa〈T,φ〉.
nyt voi nähdä, miksi jakaumia kutsutaan yleistetyiksi funktioiksi. Mahdolliset
klassinen funktio, jonka integraali

on hyvin määritelty, on vastaava jakauma F siten, että 〈F,φ〉antaa arvo tämän olennainen., On kuitenkin olemassa myös jakaumia, jotka eivät vastaa klassisia funktioita; jakaumat ovat yleisempiä. Kuten tähän mennessä pitäisi olla selvää, kanoninen esimerkki jakaumasta, joka ei vastaa klassista funktiota, on Dirac δ., Siksi me lopulta saapuvat täysin tiukka määritelmä δ jakautumista siten, että

Yleistynyt tai ”Heikko” Johdannainen
δ jakelu on vain yksi äärettömän monista jakaumat, jotka eivät
vastaa klassisen toimintoja. Näitä saadaan jonkin verran lisää erottelemalla δ jakaumien merkityksessä., Mutta miten
– jakauman käsite ratkaisee erilaistumisongelman, kuten aiemmin puhuttiin? Meidän tarvitsee vain yleistää eriyttämisen käsite sovellettavaksi jakaumiin.
Harkitse funktio f ∈ C1, niin että se on jatkuvasti derivoituva. Laskeminen käyttäen yhdentymistä osia, näemme, että

Termi suluissa katoaa koska φ, testi-toiminto, on kompakti tukea., Tämä yleistää distribution, sanoa F’, joka vastaa funktiota f’:

Tämä laskelma yleistää melko helposti jakaumat, jotka eivät vastaa klassisen funktio f., Tällä tavalla, voimme määritellä derivaatta T’ T mielessä jakaumat:

Tämä on myös joskus kutsutaan heikko derivaatta, koska se ulottuu johdannaiset toimintoja, jotka normaalisti ei olisi derivoituva. Tämä yleistyy vielä pidemmälle, korkeamman kertaluvun johdannaisiin., Voimme määritellä, että n: nnen tappion johdannaisen jakelu T T⁽ⁿ⁾, jos jälkimmäinen on jakelu niin, että

Tässä,
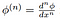
on klassisen derivaatan testi-toiminto, joka on varma,
olemassa hyvin määritelmä testata toimintoja!, Tästä seuraa, että kaikki jakaumat ovat äärettömän differentiable (merkityksessä jakaumat).
Tämä poistaa kokonaan taistelun, jonka Dirac ja muut kohtasivat erottaessaan δ-funktion. Mitä meillä on tässä määritelty, johdannainen δ vain sifts arvo toisen funktioita derivaatan nollakohdassa., Muodollisesti

Tämä tarjoaa tiukka matemaattinen kehys johdannaiset δ, joka ilmestyi kirjallisuudessa kauan ennen kuin tämä teoria syntyi.
on olemassa joukko muita toimintoja, jotka pätevät funktioihin, jotka on yleistetty koskemaan jakaumia. Niitä voidaan lisätä ja vähentää, convolved, ja muuntaa käyttämällä Laplace-ja Fourier-muunnokset., Se on kuitenkin mahdotonta määritellä kertolasku jakaumat tavalla, joka säilyttää algebra, joka koskee klassisen toiminnot (Schwartz Mahdottomuus Lause).