
Leonardo Pisan (Fibonacci) (c.1170-1250)
13-Luvulla Italian Leonardo Pisan, joka tunnetaan paremmin hänen lempinimi Fibonacci, oli ehkä kaikkein lahjakas Länsi-matemaatikko Keskiajalla. Vähän tiedetään hänen elämästään paitsi, että hän oli poika tulli offical ja, lapsena, hän matkusti ympäri Pohjois-Afrikassa hänen isänsä, jossa hän oppi Arabian matematiikka., Palattuaan Italiasta, hän auttoi levittämään tätä tietoa kaikkialla Euroopassa, mikä asettaa liikkeessä nuorentaminen Euroopan matematiikka, joka oli pysynyt pitkälti lepotilassa vuosisatojen aikana Keskiajalla.
erityisesti, vuonna 1202, hän kirjoitti vaikutusvaltainen kirja nimeltään ”Liber Abaci” (”Book of Laskenta”), jossa hän edisti käyttää Hindu-arabialainen numero järjestelmä, jossa kuvataan sen monia etuja kauppiaille ja matemaatikot keskuudessa yli kömpelö järjestelmä Roomalaisin numeroin sitten käytössä Euroopassa., Huolimatta selviä etuja, käyttöönotto järjestelmä Euroopassa oli hidasta (tämä oli loppujen aikana Ristiretkiä Islamia vastaan, aika, jossa mitään arabia oli tarkastella suuri epäily), ja arabialaiset numerot olivat jopa kielletty kaupungin Firenze vuonna 1299 sillä verukkeella, että ne oli helpompi väärentää kuin Roomalaiset numerot. Kuitenkin, järki lopulta voitti ja uusi järjestelmä otettiin käyttöön koko Euroopassa 15-luvulla, jolloin Roomalainen järjestelmä vanhentunut., Rekki merkintätapa jakeet oli myös ensimmäinen käytetty tässä työssä (vaikka seuraavat arabian käytäntö asettaa murto vasemmalla kokonaisluku).
Fibonaccin

löytö kuuluisa Fibonacci-sekvenssi
Fibonacci on parhaiten tunnettu, mutta hänen käyttöönotto eurooppaan tietyn numerosarjan, joka on sittemmin tullut tunnetuksi Fibonaccin Luvut tai Fibonaccin., Hän löysi järjestyksessä – ensin rekursiivinen numerosarja tunnettu Euroopassa – kun otetaan huomioon käytännön ongelma ”Liber Abaci”, johon kasvua hypoteettinen väestön kania, joka perustuu idealisoitu oletuksia. Hän totesi, että jokaisen kuukausittain sukupolvi, kuinka monta paria kanit lisääntynyt 1 2 3 5 8 13, jne, ja tunnistaa, miten jono eteni lisäämällä edellisen kaksi kautta (matemaattisesti, Fn = Fn-1 + Fn-2), sekvenssi, joka voisi teoriassa jatkaa loputtomiin.,
– sekvenssi, joka oli todella tunnettu Intian matemaatikot, koska 6. – Luvulla, on monia mielenkiintoisia matemaattisia ominaisuuksia, ja monia vaikutuksia ja suhteita järjestyksessä olivat löydettiin vasta useita vuosisatoja sen jälkeen, kun Fibonacci kuolemasta., Esimerkiksi, sekvenssi uusiutuu itse joitakin yllättäviä tapoja: joka kolmas F-numero on jaollinen 2 (F3 = 2), joka neljäs F-numero on jaollinen 3 (F4 = 3), joka viides F-luku on jaollinen 5 (F5 = 5), joka kuudes F-luku on jaollinen 8 (F6 = 8), joka seitsemäs F-numero on jaollinen 13 (F7 = 13), jne., Numerot järjestyksessä, on myös todettu olevan läsnä kaikkialla luonnossa: muun muassa monet lajit kukkivat kasvit on määrä terälehtiä Fibonaccin; kierre järjestelyt ananakset esiintyy 5s ja 8s, jotka pinecones vuonna 8s ja 13, ja siemenet auringonkukka päät 21s, 34s, 55 tai jopa korkeampi ehdot järjestyksessä; jne.,
Kultainen Suhde φ
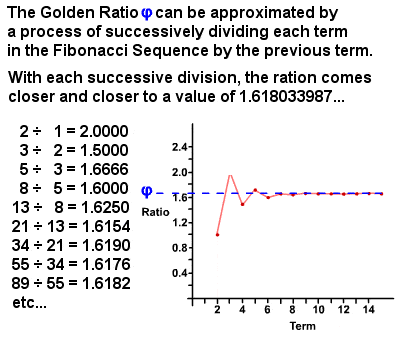
Kultainen Suhde φ voidaan johtaa Fibonaccin
Vuonna 1750, Robert Simson huomata, että suhde kunkin termin Fibonaccin edelliseen aikavälin lähestymistapaa, jossa entistä suurempi tarkkuus korkeampi ehdot, suhde on noin 1 : 1.6180339887 (se on oikeastaan järjetön määrä yhtä (1 + √5)⁄2 joka on sittemmin laskettu tuhansia desimaalin tarkkuudella)., Tätä arvoa kutsutaan Kultainen Suhde, joka tunnetaan myös nimellä Kultainen keskitie, Kultainen leikkaus, Divine Osuus, jne, ja on yleensä merkitty kreikkalainen kirjain phi φ (tai joskus kirjain Phi Φ). Pohjimmiltaan, kaksi määrät ovat Kultainen Suhde, jos suhde määrien summa suurempi määrä on yhtä suuri kuin suhde suurempi määrä pienempi. Kultainen Suhde itsessään on monia ainutlaatuisia ominaisuuksia, kuten 1⁄φ = φ – 1 (0.618…) ja φ2 = φ + 1 (2.618…), ja on olemassa lukemattomia esimerkkejä löytyy sekä luonnon ja ihmisen maailma.,
suorakulmio, jonka sivujen suhde 1 : φ tunnetaan Kultainen Suorakulmio, ja monet taiteilijat ja arkkitehdit koko historia (vuodelta muinaisessa Egyptissä ja Kreikassa, mutta erityisen suosittu Renessanssin Leonardo da Vinci ja hänen aikalaisensa) on mitoitettava niiden toimii noin käyttää Kultainen Suhde ja Kultaisia Suorakulmioita, jotka ovat yleisesti pidetään synnynnäisesti esteettisesti miellyttävä. Yhä pienempien sisäkkäisten kultaisten suorakulmioiden vastakkaisia kohtia yhdistävä kaari muodostaa logaritmisen spiraalin, joka tunnetaan kultaisena spiraalina., Kultainen leikkaus ja Kultainen Kierre löytyy myös yllättävä määrä tapauksia, Luonto, kuoret, kukkia eläinten sarvet ihmisen elinten myrsky järjestelmät loppuun galakseja.,
– Se olisi kuitenkin muistettava, että Fibonaccin oli itse asiassa vain hyvin pieni osa ”Liber Abaci” – todellakin, järjestys vain saanut Fibonacci nimi vuonna 1877, kun Eduouard Lucas päätti maksaa kunnianosoitus hänelle nimeämällä sarjan jälkeen häntä – ja että Fibonacci itse ei ole vastuussa tunnistaa mitään mielenkiintoisia matemaattisia ominaisuuksia järjestyksessä, sen suhde Kultainen keskitie ja Kultaisia Suorakulmioita ja Spiraaleja, jne.,
Lattice Kertolasku
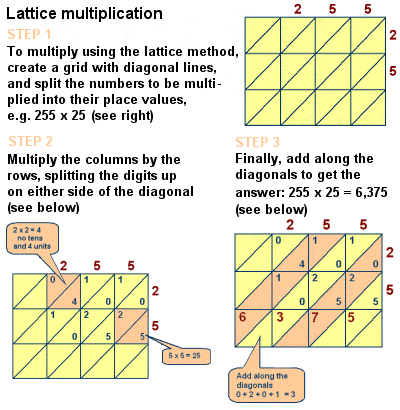
Fibonacci esitteli ristikko kertolasku eurooppaan
Kuitenkin, kirja on vaikutus keskiajan matematiikka on kiistaton, ja se sisältää myös keskusteluja useita muita matemaattisia ongelmia, kuten Kiina Remainder Theorem, täydellinen numerot ja prime numerot, kaavat aritmeettinen sarja ja neliö pyramidin numerot, Eukleideen geometrista todisteita, ja tutkimuksen samanaikainen lineaariset yhtälöt tyyliin Diofantos ja Al-Karaji., Hän myös kuvaili ristikko (tai seula) kerto-menetelmä, joka saadaan kertomalla suuri määrä, menetelmä – alun perin uranuurtajana Islamilainen matemaatikot, kuten Al-Khwarizmi – algoritmisesti vastaa pitkän kertolasku.
kumpikaan ei ollut ”Liber Abaci” Fibonaccin ainoa kirja, vaikka se oli hänen tärkein., Hänen ”Liber Quadratorum” (”Book of Squares”), esimerkiksi, on kirja algebra, joka julkaistiin vuonna 1225, jossa näkyy ilmoitus, mitä on nyt nimeltään Fibonacci identiteetti – joskus myös nimellä Brahmagupta identiteettiä jälkeen paljon aikaisemmin Intialainen matemaatikko, joka myös tuli samaan johtopäätökseen – että tuote kaksi summia kaksi ruutua on itse kahden neliöt esim.(12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,
| << Back to Medieval Mathematics | Forward to 16th Century Mathematics >> |