geometriassa monitahokas on suljettu avaruusluku, jonka kasvot ovat monikulmioita. Sanalla monitahokas on kreikkalainen alkuperä, joka tarkoittaa monia kasvoja. Seuraavassa on muutamia esimerkkejä monitahokkaista.
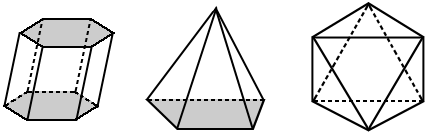
Ominaisuudet polyhedron
monikulmiot, että muodossa polyhedron ovat nimeltään kasvot. Kahden risteävän Tahkon luomia linjasegmenttejä kutsutaan reunoiksi. Vertices ovat kohtia, joissa kolme tai useampia reunoja kohtaavat.,
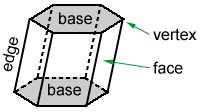
kuusikulmainen prisma edellä on monitahokas, joka on 6 sivusuunnassa kasvot, jotka ovat suunnikkaita, ja 2 kohtaa ylä-ja alareunassa, nimeltään emäkset, jotka ovat laput.
Eulerin Lause
Eulerin Lause osoittaa suhdetta määrän kasvoja, kärkipisteet ja reunat polyhedron., Siinä todetaan, että summa kasvot ja kärjet miinus määrä reunoja, aina on kaksi:
F + V – E = 2,
missä F on määrä kasvoja, V on solmujen lukumäärä ja E on määrä reunat polyhedron.
Esimerkki:
Varten kuusikulmainen prisma yllä, F = 8 (kuusi sivusuunnassa kasvot + kaksi emäkset), V = 12, ja E = 18:
8 + 12 – 18 = 2
Luokitukset polyhedra
Polyhedra voidaan luokitella monin tavoin. Ne voidaan luokitella esimerkiksi säännöllisiksi ja epäsäännöllisiksi monitahokkaiksi., Säännöllinen monitahokas on monitahokas, jonka kasvot ovat kaikki congruent säännölliset monikulmiot; tahansa monitahokas, joka ei täytä näitä ehtoja pidetään epäsäännöllinen.
Polyhedra voidaan myös luokitella kupera ja kovera. Koveralla monitahokkaalla on ainakin yksi kasvo, joka on kovera monikulmio. Monitahokas, joka ei ole kovera, on kupera. Polyhedra voidaan luokitella myös sen mukaan, kuinka monta tahkoa sillä on. Esimerkiksi, tetrahedron on 4 kohtaa, on pentahedron on 5 kohtaa, ja heksaedrin on 6 kasvot.,
seuraava on luettelo termeistä, joita käytetään usein kuvaamaan monitahokkaita niiden ominaisuuksien perusteella.
Prismat
Prismat ovat polyhedra, että on kaksi congruent kasvot, nimeltään emäkset, makaa rinnakkain lentokoneita. Prisma on tyypillisesti nimetty monikulmioisten emästensä muodon mukaan. Sivuttaispinnat (sivut, jotka eivät ole emäksiä) ovat parallelogrammeja, suorakulmioita tai neliöitä.,
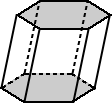
| Säännöllinen prisma | Epäsäännöllinen prisma |
|---|---|
 |
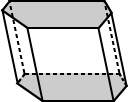 |
| Perustan säännöllinen kuusikulmainen prisma edellä on tukikohtia, jotka ovat säännöllisesti laput. | edellä olevan kuusikulmaisen prisman emäkset ovat epäsäännöllisiä kuusikulmioita. |
Pyramidit
Pyramidit ovat polyhedra, joka on monikulmio, koska sen pohja ja kolmioita, kuten kaikki sen muita kasvoja.Pyramidi on myös tyypillisesti nimetty sen monikulmioisen pohjan muodon mukaan.,
| Säännöllinen pyramid | Epäsäännöllinen pyramid |
|---|---|
 |
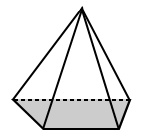 |
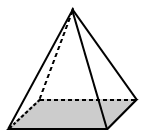
| Pohja neliö pyramidi on, että pohja on neliö (säännöllinen monikulmio). | pohjan puolisuunnikkaan muotoinen pyramidi on puolisuunnikkaan kanssa eriarvoiseen sivut (niin se on epäsäännöllinen monikulmio). |
Säännöllinen polyhedra
säännöllinen monitahokas on monitahokas, jonka kasvot ovat kaikki yhteneviä säännöllisiä monikulmioita., Säännöllinen monitahokas on nimetty sen kasvojen lukumäärän perusteella. Monitahokkaita on vain viisi, jotka ovat säännöllisiä monitahokkaita; näitä kutsutaan Platonisiksi kiintoaineiksi.
viisi Platonin kiintoaineita
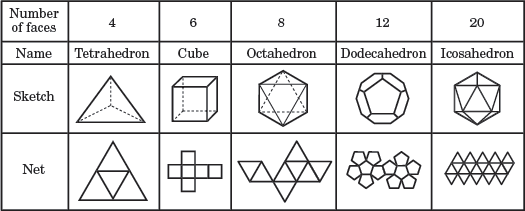
yllä olevassa kuvassa, jokainen säännöllinen polyhedra on nimetty perustuu sen määrä kasvoja. Jokaisen sketsin alla olevassa verkossa on 2D-Kuva kaikista monitahokkaan kasvoista.
useimpia säännöllisiä prismoja ei yleensä pidetä säännöllisinä monitahokkaina., Kuutio on ainoa säännöllinen prisma, joka voidaan luokitella myös tavalliseksi monitahokkaaksi.
Lisäksi, säännöllinen tetraedri on ainoa säännöllinen pyramidi, joka on myös säännöllinen monitahokas.