Kun ”normaali” osa sisältää jakeet joko osoittaja tai nimittäjä, tai molemmat, sitten katsomme, että se on monimutkainen osa. Tämä fraktio tunnetaan myös yhdistelmäfraktiona.
on olemassa kaksi menetelmää, joilla yksinkertaistetaan tällaista fraktiota.
Menetelmä 1
Keskeiset vaiheet:
- Luoda yhden murtoluvun osoittaja ja nimittäjä.,
- Sovellettava jako sääntö jakeet kertomalla osoittaja, jonka vastavuoroinen tai käänteinen nimittäjä.
- yksinkertaistaa tarvittaessa.
Menetelmä 2
Keskeiset vaiheet:
- Löytää Vähiten Yhteistä Nimittäjää (LCD) kaikki nimittäjät monimutkainen jakeet.
- Kerrotaan tämä LCD-osoittaja ja nimittäjä monimutkainen osa.
- yksinkertaistaa tarvittaessa.,
Kun menee yli muutamia esimerkkejä, sinun pitäisi ymmärtää, että Tapa 2 on paljon parempi kuin Menetelmä 1, koska lähes aina se vaatii vähemmän vaiheita saada lopullista vastausta.
Esimerkkejä siitä, Miten Yksinkertaistaa Monimutkaisia Jakeet
Esimerkki 1: Yksinkertaistaa monimutkainen murto alla.
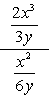
- Käyttämällä Menetelmää: 1
Sekä osoittaja ja nimittäjä monimutkainen osa on jo ilmaissut yksittäisinä osina. Tämä on mahtavaa!,

seuraava askel tehdä, on sovellettava jako sääntö kertomalla osoittaja, jonka vastavuoroinen nimittäjä. Lopeta peruuttamalla yhteisiä tekijöitä saada lopullinen vastaus.
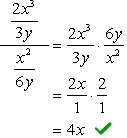
- Käytetään Menetelmää 2
LCD-näytön koko ongelma on, että LCD-näytön ylä-ja alareunassa nimittäjiä.,

Koska LCD-3y ja 6y on vain \textbf{6y}, me nyt moninkertaistaa monimutkainen osoittaja ja nimittäjä tässä LCD-näytössä. Tämän jälkeen voimme odottaa, että ongelma supistetaan yhteen murto-osaan, jota voidaan yksinkertaistaa tavalliseen tapaan.
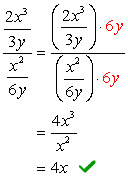
Esimerkki 2: Yksinkertaistaa monimutkainen murto alla.,
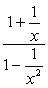
- Käyttämällä Menetelmää: 1
tämä menetelmä, haluamme luoda yksittäinen osa sekä osoittaja ja nimittäjä. On selvää, että tämä ongelma vaatii meitä tekemään sen ensin, ennen kuin suoritamme jaoksen.
Lisää jakeet osoittajaan ja vähennä nimittäjään kuuluvat.,
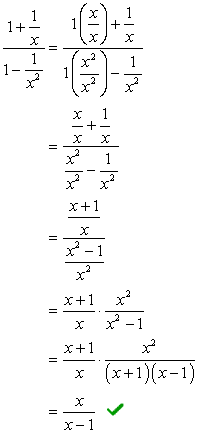
- Käytetään Menetelmää 2
tarkastellaan nimittäjiä \large{x} ja \large{x^2}, sen LCD-näyttö on \large{x^2} Kerrotaan ylä-ja alareunassa tässä LCD-näytössä.
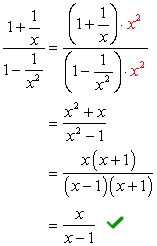
Esimerkki 3: Yksinkertaistaa monimutkainen murto alla.,
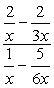
- Käyttämällä Menetelmää: 1
Luo yhden jakeet sekä osoittaja ja nimittäjä, sitten seuraa jakamalla jakeet.
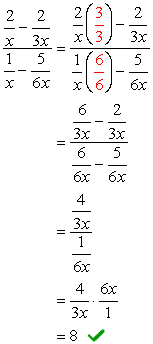
- Käytetään Menetelmää 2
yleistä LCD nimittäjiä on \color{red}6x. Käytä tätä lisääntyä läpi ylä-ja alareunassa ilmaisuja.,
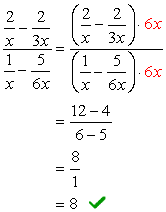
Esimerkki 4: Yksinkertaistaa monimutkainen murto alla.
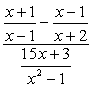
tähän ongelmaan, aiomme käyttää Menetelmää 1 vain.
ongelma edellyttää voit käyttää FOLIO-menetelmää (kerto kaksi binomials) ja yksinkertainen factorization of trinomial. Se voi aluksi näyttää hieman pelottavalta; mutta jos kiinnität huomiota yksityiskohtiin, takaan sinulle, että se ei ole niin huono.,
Jos huomaat, monimutkainen nimittäjä on jo siinä muodossa, että haluamme – ottaa yksi murto-symboli. Tämä tarkoittaa, että meidän täytyy työskennellä hieman monimutkainen Osoittaja. Seuraava askel olisi muuttaa monimutkainen Osoittaja ”yksinkertainen” tai yksi murto.
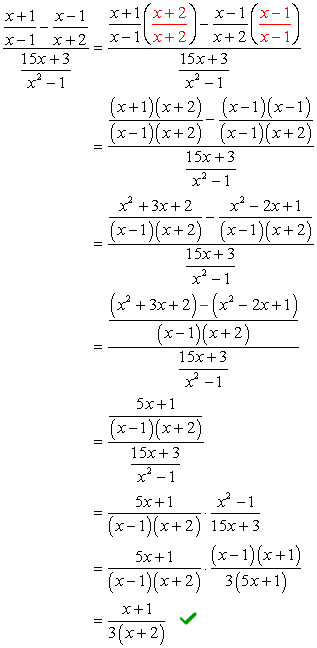
Esimerkki 5: Yksinkertaistaa monimutkainen murto alla.
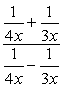
tähän ongelmaan, aiomme käyttää Menetelmää 2 vain.,
Huomioi, että LCD-näytössä kaikki nimittäjät on vain \color{red}12x. Käytä tätä yhteistä kerroin sekä ylä-ja alareunassa ilmaisuja.
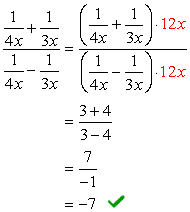
Käytännössä Laskentataulukoita
saatat myös olla kiinnostunut:
Kertomalla Monimutkainen Jakeet
Jakamalla Monimutkainen Numerot