Tanulási Eredmények
- megismerjék a történelem helyzeti száma rendszerek
- Azonosítani bázisok használt száma rendszerek történetileg
- Convert számok között bázisok
- a két különböző módszer, mely a számok között bázisok
Háttér
képzelhetik, hogy a fejlesztés egy alap rendszer egy fontos lépés, hogy a számolás folyamat hatékonyabb., Saját bázis-ten rendszerünk valószínűleg abból a tényből ered, hogy 10 ujjunk van (beleértve a hüvelykujját is) két kézzel. Ez természetes fejlődés. Más civilizációknak azonban a tízen kívül számos bázisuk volt. Például Queensland bennszülöttei egy bázis-két rendszert használtak, a következőképpen számolva: “egy, kettő, kettő, egy, kettő, sok.”Néhány Modern dél-amerikai törzsnek van egy bázis-öt rendszere, amely így számol: ” egy, kettő, három, négy, kéz, kéz és egy, kéz és kettő” stb. A babiloniak bázis-hatvan (sexigesimal) rendszert használtak., Ebben a fejezetben egy olyan civilizáció konkrét példájával foglalkozunk, amely valójában 10-től eltérő alaprendszert használt.
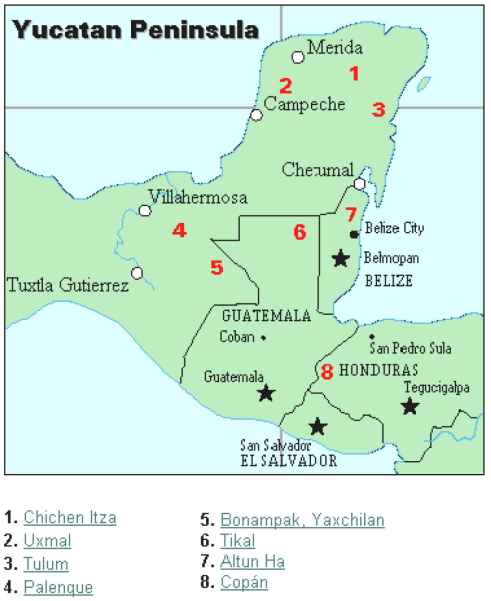A maja civilizáció általában I.E. 1500-tól 1700-ig nyúlik vissza. A mexikói Yucatan-félsziget (lásd a 16.ábrát) az ókori világ egyik legfejlettebb civilizációjának fejlődésének helyszíne volt. A majáknak kifinomult rituális rendszere volt, amelyet egy papi osztály felügyelt. Ez a papcsoport filozófiát fejlesztett ki az idővel, mint isteni és örök., A naptár és a hozzá kapcsolódó számítások tehát nagyon fontosak voltak a papi osztály rituális életében, így a maja népében is. Tény, hogy sok mindent tudunk erről a kultúráról a naptár-és csillagászati adataikból. Egy másik fontos információforrás a Majánokról Diego de Landa Atya írásai, akik 1549-ben misszionáriusként mentek Mexikóba.
két számrendszert fejlesztettek ki a maják—az egyik a köznép, a másik a papok számára., Ez a két rendszer nemcsak különböző szimbólumokat használt,hanem különböző alaprendszereket is. A papok számára a számrendszert rituálé irányította. Az év napjait isteneknek tartották, így a napok formális szimbólumai díszítették a fejeket, mint például a bal oldali minta, mivel az alapnaptár 360 napra épült, a papi számrendszer vegyes alaprendszert használt, amely 20 és 360 szorzót alkalmaz. Ez zavaró rendszert eredményez, amelynek részleteit kihagyjuk.,/td>
The Mayan Number System
Instead, we will focus on the numeration system of the “common” people, which used a more consistent base system., Mint korábban említettük, a maják egy base-20 rendszert használtak, az úgynevezett “vigesimal” rendszert. A rendszerünkhöz hasonlóan pozicionális, ami azt jelenti, hogy egy numerikus szimbólum pozíciója jelzi a helyértékét. A következő táblázatban látható a hely értéke függőleges formátumban.
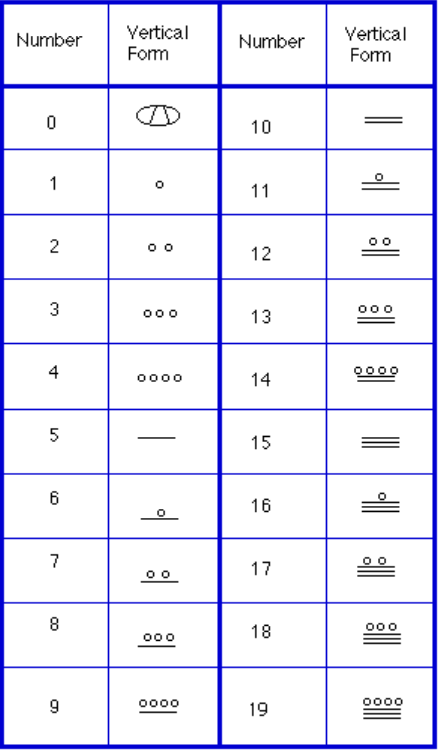
a számok leírásához csak három szimbólumra volt szükség ebben a rendszerben. Egy vízszintes sáv az 5-ös mennyiséget, egy pont az 1-es mennyiséget, egy speciális szimbólum (feltételezés szerint héj) pedig a nullát képviselte., Lehet, hogy a maja rendszer használta először a nullát helyőrzőként / számként. Az első 20 szám a jobb oldali táblázatban látható.
ellentétben a mi rendszerünkkel, ahol a hely jobbra indul, majd balra mozog, a maja rendszerek a függőleges tájolás aljára helyezik azokat, és a helyérték növekedésével felfelé mozognak.
Ha a számokat függőleges formában írják, soha nem lehet több, mint négy pont egyetlen helyen. A maja számok írásakor minden öt pontból álló csoport egy sáv lesz., Is, soha nem lehet több, mint három bár egyetlen helyen … négy bár lenne alakítani egy pont a következő helyen fel. Ez ugyanaz, mint 10 egyre alakítjuk a 1 A következő helyen fel, amikor magunkkal során kívül.
példa
mi ennek a számnak az értéke, amely függőleges formában jelenik meg?
példa
mi a következő Maja szám értéke?,
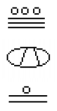
próbálja ki
konvertálja az alábbi Maja számot a 10-es alapra.,
Példa
Convert az alap 10 szám 357510, hogy Maja számok.
vegye figyelembe, hogy az előző példában egy új jelölést használtunk, amikor 8,18,1520-at írtunk. A vesszők a három szám között 8, 18 és 15 most elválasztják a helyértékeket számunkra, hogy elkülöníthessük őket egymástól. Ez a vessző használata kissé eltér attól, ahogyan a decimális rendszerben használják őket. Amikor egy számot a 10-es alapba írunk, mint például a 7,567,323, a vesszőket elsősorban segédként használják a szám egyszerű olvasásához, de nem különítik el egymástól az egypontos értékeket., Szükségünk lesz erre a jelölésre, ha az általunk használt alap nagyobb, mint 10.
10-nél nagyobb bázisú számok írása
Ha egy szám alapja nagyobb, mint 10, különítsen el minden” számjegyet ” vesszővel, hogy a számjegyek elválasztása egyértelmű legyen.
például a 20-as alapban írja be a megfelelő számot 17 × 202 + 6 × 201 + 13 × 200, 17,6,1320-at írnánk.
a következő videóban további példákat mutatunk be arról, hogyan lehet számokat írni Maja számokkal, valamint a maja nyelven írt számokat 10 alapformára konvertálni.,
a következő videó további példákat mutat az alap 10 számok Maja számokká történő konvertálására.
Maja Számok hozzáadása
A Maja számok összeadásakor elfogadunk egy olyan sémát, amelyet a maják valószínűleg nem használtak, de ami megkönnyíti az életet számunkra.
Example
Add, In Maja, the numbers 37 and 29:
Próbáld
Próbálja ki 174 78 Maja által első konvertáló, hogy Maja számok majd dolgozni teljesen a rendszeren belül. Ne adja hozzá a base-ten-t (decimális) a végéig, amikor ellenőrzi a munkáját.
az utolsó videóban további példákat mutatunk be a maja számok hozzáadására.,
ebben a modulban röviden vázoltuk a számok és a számlálási rendszer fejlesztését, a hangsúly a “rövid” részre helyeződött. Számos információ-és kutatási forrás található, amelyek sok kötetet töltenek be ebben a témában. Sajnos nem kezdhetjük el közeledni ahhoz, hogy lefedjük az összes információt, ami odakint van.
csak a számok fejlődésével és a számolással kapcsolatos kutatások és információk gazdagságának felszínét karcoltuk meg az emberi történelem során., Fontos megjegyezni, hogy a rendszer, amelyet minden nap használunk, több ezer éves fejlődés eredménye. Számos civilizáció és kultúra hozzájárulását képviseli. Nem jön le hozzánk az égből, az istenek ajándéka. Ez nem egy Tankönyvkiadó létrehozása. Ez valóban olyan emberi, mint mi, mint a többi matematika. Minden szimbólum, képlet és szabály mögött emberi arc található, vagy legalábbis keresett.
továbbá reméljük, hogy most már van egy alapvető elismerését, hogy milyen érdekes, változatos számrendszerek kaphat., Is, biztosak vagyunk benne, hogy Ön is elkezdte felismerni, hogy a saját számrendszerünket magától értetődőnek vesszük annyira, hogy amikor megpróbálunk alkalmazkodni más rendszerekhez vagy alapokhoz, akkor valóban arra kell koncentrálnunk, és gondolkodnunk, hogy mi folyik itt.