az 5 Klaszterező algoritmusok adatok a tudósoknak tudniuk kell

nemrég elindítottam egy könyvközpontú oktatási hírlevelet. A Book Dives egy kéthetente megjelenő hírlevél, ahol minden új kiadáshoz belemerülünk egy nem-fikciós könyvbe. Megtanulod a könyv alapvető tanulságait, és hogyan alkalmazhatod őket a való életben. Itt feliratkozhat rá.

a Csoportosítás gépi tanulási technika, amely magában foglalja az adatpontok csoportosítását. Mivel egy sor adatpont, tudjuk használni a klaszterezés algoritmus osztályozza az egyes adatok pont egy adott csoportba., Elméletileg az ugyanazon csoportba tartozó adatpontoknak hasonló tulajdonságokkal és/vagy jellemzőkkel kell rendelkezniük, míg a különböző csoportokban lévő adatpontoknak nagyon eltérő tulajdonságokkal és/vagy jellemzőkkel kell rendelkezniük. A klaszterezés a felügyelet nélküli tanulás egyik módszere, amely számos területen alkalmazott statisztikai Adatelemzés közös technikája.

az Adattudományban a klaszterezés elemzésével értékes betekintést nyerhetünk adatainkból, ha megnézzük, hogy az adatpontok milyen csoportokba esnek, amikor klaszterező algoritmust alkalmazunk., Ma 5 népszerű klaszterezési algoritmust fogunk megvizsgálni, amelyeket az adattudósoknak tudniuk kell, valamint azok előnyeit és hátrányait!

K-azt jelenti, klaszterezés

k-azt jelenti, talán a legismertebb klaszterezés algoritmus. Sok bevezető adattudományban és gépi tanulásban tanítják. Ez könnyen érthető, és végre a kódot! Nézze meg az alábbi ábrát illusztráció.,

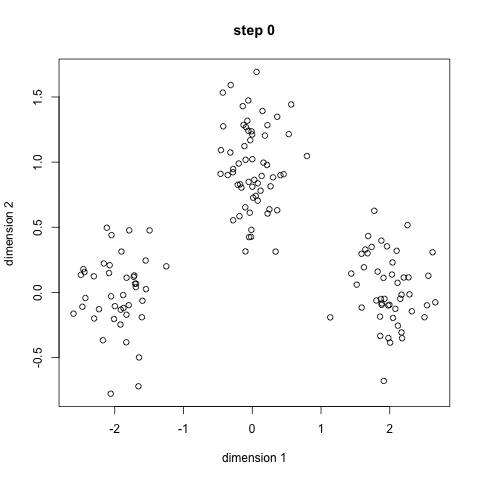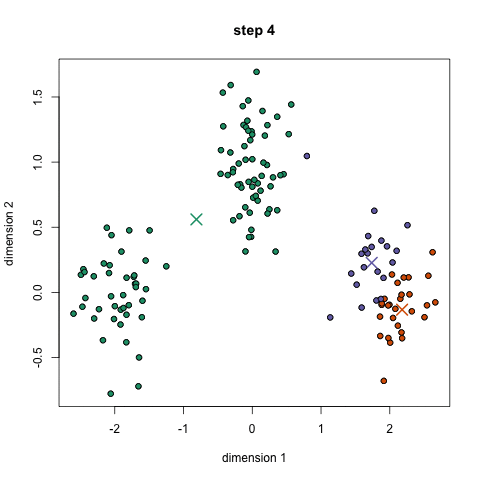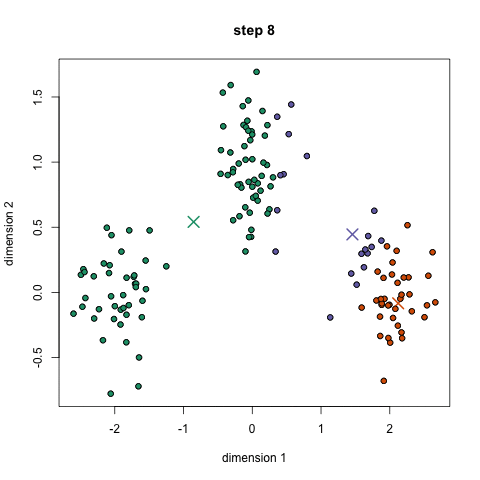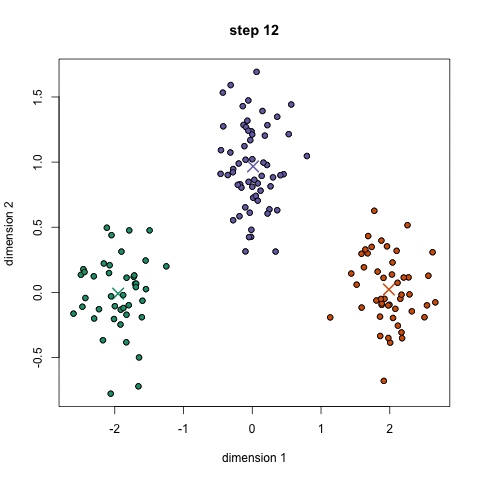
1. kezdeni, először válassza ki, hogy hány osztályok/csoportok használata véletlenszerűen inicializálja a megfelelő center pontot. Ahhoz, hogy kitaláljuk, az osztályok száma használni, ez jó, hogy egy gyors pillantást az adatokat, majd próbálja azonosítani a különböző csoportosítások. A középpontok az egyes adatpontvektorokkal azonos hosszúságú Vektorok, a fenti ábrán pedig az “X” – ek.,
2. minden adatpontot úgy osztályoznak, hogy kiszámítják az adott pont és az egyes csoportközpontok közötti távolságot, majd osztályozzák azt a pontot, amely abban a csoportban van, amelynek középpontja a legközelebb van hozzá.
3. ezen Osztályozott pontok alapján újraszámoljuk a csoportközpontot a csoport összes vektorának átlagával.
4. ismételje meg ezeket a lépéseket egy meghatározott számú iterációhoz, vagy amíg a csoportközpontok nem változnak sokat az iterációk között. Azt is választhatja, hogy véletlenszerűen inicializálja a csoportközpontokat néhányszor, majd válassza ki azt a futást, amely úgy néz ki, hogy a legjobb eredményeket nyújtja.,

K-azt jelenti, az az előnye, hogy elég gyors, mint minden, amit igazán csinál a számítás közötti távolság pontok és csoport központok; nagyon kevés számítás! Így lineáris komplexitása O (n).

másrészt a K-eszközöknek néhány hátránya van. Először ki kell választania, hogy hány csoport/osztály van. Ez nem mindig triviális, ideális esetben egy klaszterező algoritmussal azt szeretnénk, ha kitalálná ezeket nekünk, mert a lényeg az, hogy betekintést nyerjünk az adatokból., A K-means a klaszterközpontok véletlenszerű kiválasztásával is kezdődik, ezért az algoritmus különböző futásain eltérő klaszterezési eredményeket eredményezhet. Így előfordulhat, hogy az eredmények nem ismételhetők, nincs következetesség. Más klaszter módszerek következetesebbek.

A K-mediánok egy másik, a K-eszközökkel kapcsolatos csoportosítási algoritmus, kivéve, ha a csoport középpontjait a csoport medián vektorát használjuk., Ez a módszer kevésbé érzékeny a kiugró értékekre( a Medián használata miatt), de sokkal lassabb a nagyobb adatkészleteknél, mivel a medián vektor kiszámításakor minden iterációra válogatásra van szükség.

átlagos-Shift fürtözés

átlagos shift fürtözés egy csúszó-ablak alapú algoritmus, amely megpróbálja megtalálni sűrű területek adatpontok. Ez egy centroid alapú algoritmus, ami azt jelenti, hogy a cél az, hogy keresse meg a központ pontjai minden csoport/osztály, amely úgy működik, frissítésével jelöltek center pont, hogy az átlag a pontokat a csúszó-ablak., Ezeket a jelölt ablakokat ezután utófeldolgozási szakaszban szűrjük, hogy megszüntessük a Közel-duplikációkat, létrehozva a végső középpontokat és azok megfelelő csoportjait. Nézze meg az alábbi ábrát illusztráció.

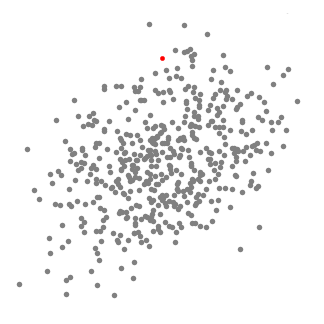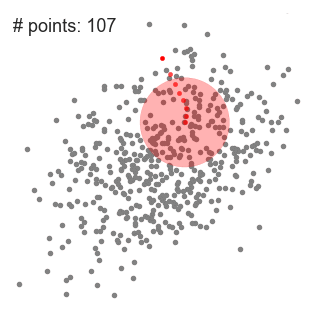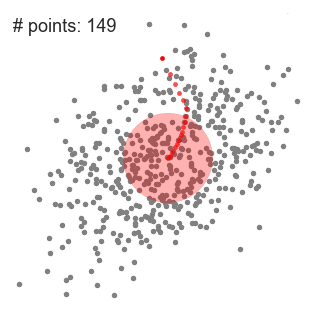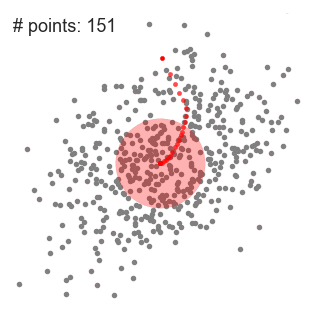
1. elmagyarázni, Hogy értem-shift figyelembe vesszük, hogy egy meghatározott pontot, a két-dimenziós térben, mint a fenti ábrán., Kezdjük egy kör alakú csúszó ablak közepén egy pont C (véletlenszerűen kiválasztott), amelynek sugara r, mint a kernel. A Mean shift egy hegymászó algoritmus, amely magában foglalja a kernel iteratív áthelyezését egy nagyobb sűrűségű régióra minden lépésnél a konvergenciáig.
2. minden iterációnál a csúszóablak a nagyobb sűrűségű régiók felé tolódik el úgy, hogy a középpontot az ablakon belüli pontok átlagára tolja (innen a név). A tolóablakon belüli sűrűség arányos a benne lévő pontok számával., Természetesen az ablak pontjainak átlagára váltva fokozatosan a magasabb pontsűrűségű területek felé halad.
3. folytatjuk a csúszó ablakot az átlagnak megfelelően, amíg nincs olyan irány, amelyen a váltás több pontot képes befogadni a kernel belsejében. Nézze meg a fenti ábrát; addig mozgatjuk a kört, amíg már nem növeljük a sűrűséget (azaz az ablakban lévő pontok számát).
4. ez az 1-3. lépésfolyamat sok csúszó ablakkal történik, amíg az összes pont egy ablakon belül nem található., Ha több csúszó ablak átfedésben van, a legtöbb pontot tartalmazó ablak megmarad. Az adatpontokat ezután a csúszó ablak szerint csoportosítják, amelyben tartózkodnak.

az alábbiakban bemutatjuk az egész folyamatot a végponttól a végéig az összes csúszó ablakkal. Minden fekete pont a csúszó ablak centroidját, minden szürke pont pedig adatpont.,

ellentétben a K-jelenti klaszterezés, nincs szükség, hogy válassza ki a klaszterek száma, mint átlagos-Shift automatikusan felfedezi ezt. Ez hatalmas előny. Az a tény, hogy a klaszter központok közelednek a maximális sűrűség pontjaihoz, szintén nagyon kívánatos, mivel nagyon intuitív megérteni és jól illeszkedik a természetesen adatvezérelt értelemben., A hátrány az, hogy az “R” ablakméret/sugár kiválasztása nem triviális lehet.

sűrűség-alapú térbeli klaszterezés Alkalmazások zaj (DBSCAN)

DBSCAN egy sűrűség-alapú klaszterezett algoritmus hasonló átlagos-shift, de egy pár figyelemre méltó előnye. Nézze meg egy másik díszes grafika alatt, és kezdjük el!,

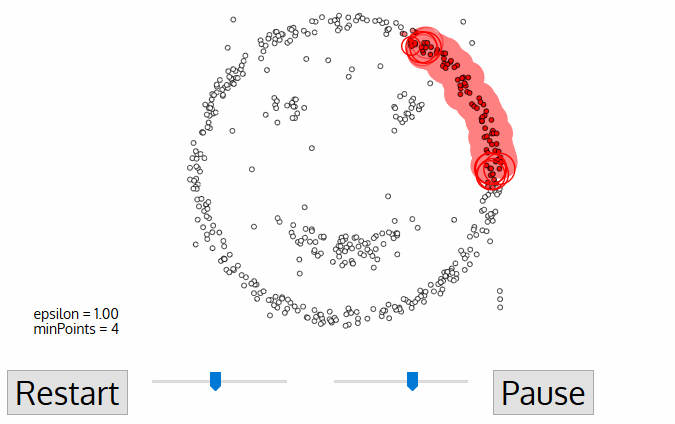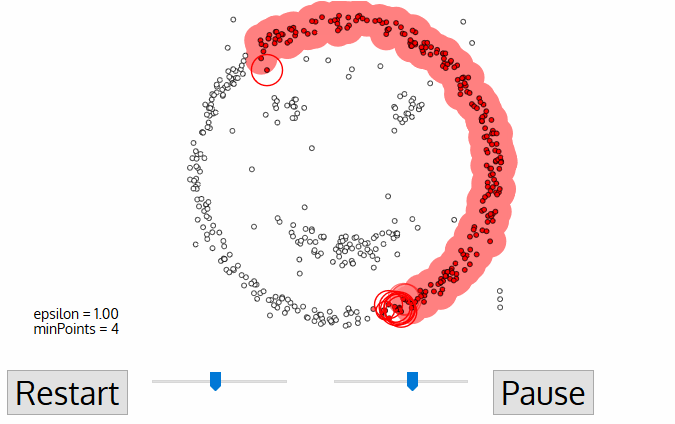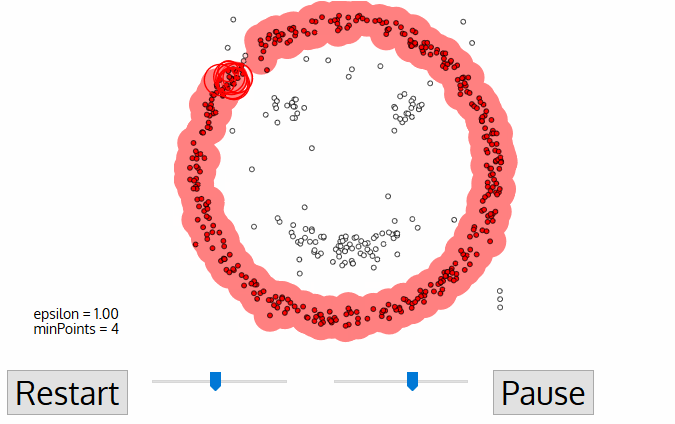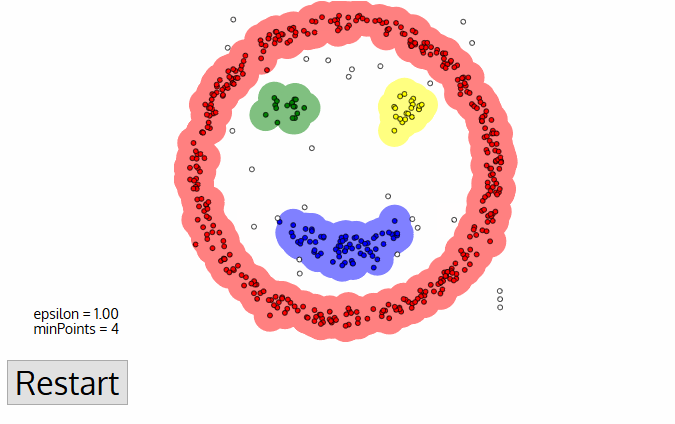
1. dbscan egy tetszőleges kiindulási adatponttal kezdődik, amelyet még nem látogattak meg. Ennek a pontnak a szomszédságát Epsilon ε távolsággal extraháljuk (az ε távolságon belüli összes pont szomszédsági pont).,
2. ha elegendő számú pont van ezen a környéken (minPoints szerint), akkor a klaszterezési folyamat elindul, és az aktuális adatpont lesz az új klaszter első pontja. Ellenkező esetben a pontot zajként jelöljük (később ez a zajos pont a klaszter részévé válhat). Mindkét esetben ez a pont “meglátogatott”.
3. az új klaszter ezen első pontjára az ε távolságon belüli pontok is ugyanazon klaszter részévé válnak., Ezt az eljárást, amely szerint az ε szomszédság minden pontja ugyanahhoz a klaszterhez tartozik, megismételjük az összes új pont esetében, amelyeket éppen hozzáadtak a klasztercsoporthoz.
4. ezt a 2. és 3. lépésfolyamatot addig ismételjük, amíg a klaszter összes pontját meg nem határozzuk, azaz a klaszter ε szomszédságában lévő összes pontot meglátogattuk és címkéztük.
5. miután végeztünk az aktuális klaszterrel, egy új, nem látogatott pontot kapunk és feldolgozunk, ami egy további klaszter vagy zaj felfedezéséhez vezet. Ez a folyamat mindaddig megismétlődik, amíg az összes pontot látogatottnak nem jelölik., Mivel ennek végén minden pontot Meglátogattak, minden pontot egy klaszterhez tartozónak vagy zajnak jelölnek.

DBSCAN jelent néhány nagy előnye más klaszterezési algoritmusok. Először is, egyáltalán nem igényel PE-set klaszterek számát. A kiugró értékeket zajként is azonosítja, ellentétben az átlagos eltolódással, amely egyszerűen egy klaszterbe dobja őket, még akkor is, ha az adatpont nagyon eltérő. Továbbá, megtalálja önkényesen méretű, önkényesen alakú klaszterek elég jól.,

a DBSCAN fő hátránya, hogy nem működik olyan jól, mint mások, ha a klaszterek változó sűrűségűek. Ennek oka az, hogy az ε távolságküszöb és a szomszédos pontok azonosítására szolgáló minpontok beállítása klaszterenként változik, amikor a sűrűség változik. Ez a hátrány nagyon nagy dimenziós adatokkal is előfordul, mivel az ε távolságküszöb ismét kihívást jelent a becsléshez.,

elvárás-Maximalizáció (EM) klaszterezés segítségével Gauss keverék modellek (GMM)

A K-eszközök egyik fő hátránya a klaszterközpont átlagértékének naiv használata. Láthatjuk, hogy miért nem ez a legjobb módja a dolgok elvégzésének az alábbi képre nézve. A bal oldalon, úgy néz ki, teljesen nyilvánvaló, hogy az emberi szem, hogy van két kör alakú klaszterek különböző sugarú ” középre azonos átlagos. A K-Means ezt nem tudja kezelni, mert a klaszterek átlagértékei nagyon közel vannak egymáshoz., A K-eszközök akkor is kudarcot vallnak, ha a klaszterek nem körkörösek, ismét az átlag klaszterközpontként történő használata következtében.

Gauss-féle Keverék Modellek (Felhasználás) több rugalmasság, mint a K-means. A GMM-ekkel feltételezzük, hogy az adatpontok Gaussian elosztva vannak; ez kevésbé korlátozó feltételezés, mint azt mondani, hogy kör alakúak az átlag használatával., Így két paraméterünk van a klaszterek alakjának leírására: az átlag és a szórás! Két dimenzióban példát véve ez azt jelenti, hogy a klaszterek bármilyen elliptikus alakot vehetnek fel (mivel standard eltérés van mind az x, mind az y irányban). Így minden Gauss-eloszlást egyetlen klaszterhez rendelnek.

Az egyes klaszterek Gauss paramétereinek (pl. az átlag és a szórás) megkereséséhez egy optimalizáló algoritmust használunk, az úgynevezett elvárás-Maximizációt (EM)., Vessen egy pillantást az alábbi ábrára, mint a Gaussiak klaszterekbe való felszerelésének illusztrációjára. Ezután folytathatjuk a várakozás–Maximalizálás klaszterezését GMM-ek segítségével.

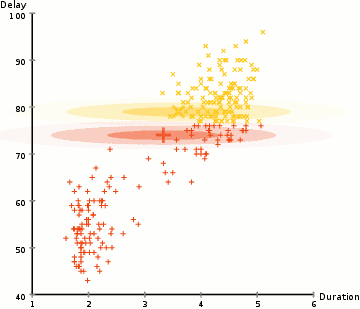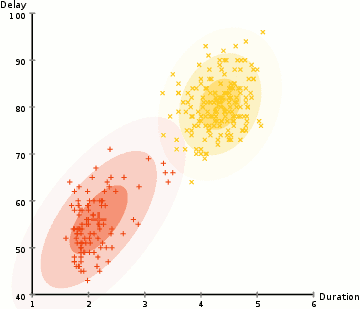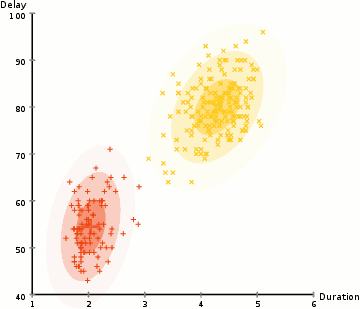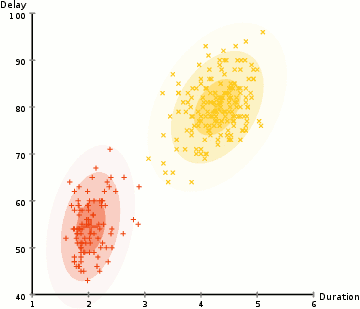
1. kezdjük a klaszterek számának kiválasztásával (mint például a K-means does), majd véletlenszerűen inicializáljuk az egyes klaszterek Gauss eloszlási paramétereit., Megpróbálhatunk jó találgatást adni a kezdeti paraméterekhez, ha gyorsan megnézzük az adatokat is. Bár vegye figyelembe, amint az a fenti ábrán látható, ez nem 100% – ban szükséges, mivel a Gaussiak nagyon szegényként kezdik el, de gyorsan optimalizálják őket.
2. tekintettel ezekre a Gauss-eloszlásokra az egyes klasztereknél, számítsa ki annak valószínűségét, hogy minden adatpont egy adott klaszterhez tartozik. Minél közelebb van egy pont a Gauss-központhoz, annál valószínűbb, hogy a klaszterhez tartozik., Ennek intuitív értelemben kell lennie, mivel Gauss-eloszlással feltételezzük, hogy az adatok többsége közelebb áll a klaszter középpontjához.
3. ezen valószínűségek alapján kiszámítunk egy új paraméterkészletet a Gauss-eloszlásokhoz, hogy maximalizáljuk a klasztereken belüli adatpontok valószínűségét. Ezeket az új paramétereket az adatpontpozíciók súlyozott összegével számítjuk ki, ahol a súlyok az adott klaszterhez tartozó adatpont valószínűségei., Ennek vizuális magyarázata érdekében megnézzük a fenti ábrát, különösen a sárga klasztert példaként. Az eloszlás indul véletlenszerűen az első iteráció, de láthatjuk, hogy a legtöbb sárga pont a jobb oldalon, hogy az eloszlás. Amikor kiszámítjuk a valószínűségekkel súlyozott összeget, annak ellenére, hogy vannak pontok a központ közelében, a legtöbbjük a jobb oldalon van. Így természetesen az eloszlás átlaga közelebb kerül a pontok halmazához. Azt is láthatjuk, hogy a legtöbb pont “jobb felső-bal alsó-bal”., Ezért a szórás megváltozik, hogy ellipszist hozzon létre, amely jobban illeszkedik ezekhez a pontokhoz, hogy maximalizálja a valószínűségekkel súlyozott összeget.
4. a 2. és 3. lépést iteratívan ismételjük a konvergenciáig, ahol az eloszlások nem sokat változnak iterációtól iterációig.

A GMMs használatának 2 fő előnye van. Először is a GMM-ek sokkal rugalmasabbak a klaszter kovariancia szempontjából, mint a K-eszközök; a szórási paraméter miatt a klaszterek ellipszis alakúak lehetnek, ahelyett, hogy körökre korlátozódnának., A K-Means valójában egy speciális GMM eset, amelyben minden klaszter kovarianciája minden dimenzió mentén megközelíti a 0-t. Másodszor, mivel a GMM-ek valószínűségeket használnak, adatpontonként több klaszter is lehet. Tehát, ha egy adatpont két átfedő klaszter közepén van, egyszerűen meghatározhatjuk annak osztályát, mondván, hogy X-százalék az 1. osztályhoz, Y-százalék pedig a 2. osztályhoz tartozik. Vagyis a GMMs támogatja a vegyes tagságot.

Agglomeratív hierarchikus klaszterezés

hierarchikus klaszterezési algoritmusok 2 kategóriába tartoznak: felülről lefelé vagy alulról felfelé., Alulról felfelé algoritmusok kezelni minden adatot, ahogy egyetlen klaszter az elején, majd egymás után merge (vagy agglomerátum) pár klaszterek, amíg az összes klaszterek volna beolvadnak egy halmaz, amely tartalmazza mindazokat az adatokat. Alulról felfelé hierarchikus klaszterezés ezért az úgynevezett hierarchikus agglomeratív klaszterezés vagy HAC. A klaszterek hierarchiáját fa (vagy dendrogram) képviseli. A fa gyökere az egyedülálló klaszter, amely összegyűjti az összes mintát, a levelek pedig csak egy mintával rendelkező klaszterek., Nézze meg az alábbi ábrát az illusztráció, mielőtt továbblépne, hogy az algoritmus lépései

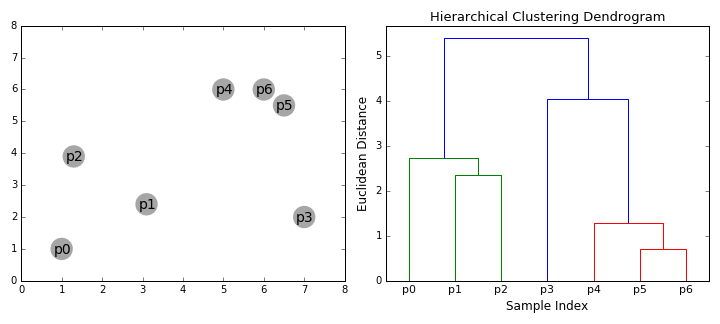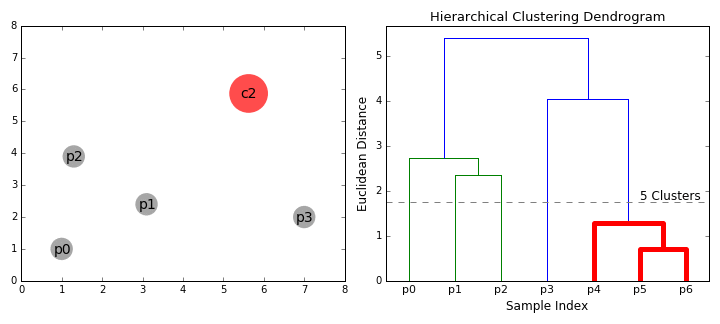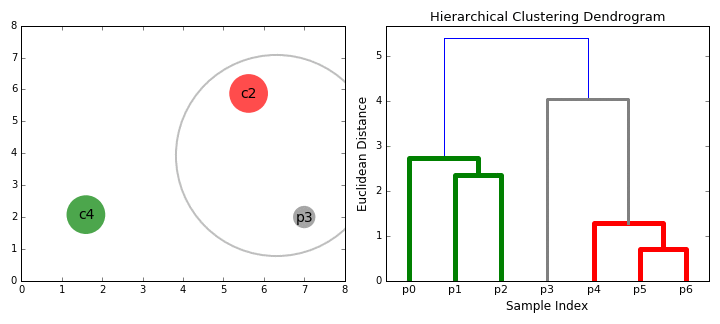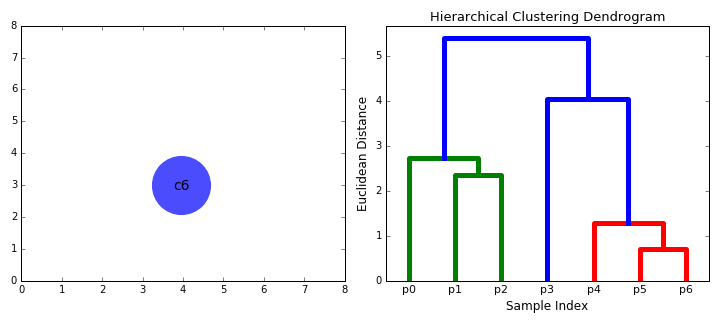
1. kezdjük azzal, hogy kezelni minden adatot, ahogy egyetlen klaszter én.e, ha X adatokat az adatkészlet akkor X klaszterek. Ezután kiválasztunk egy távolságmérőt, amely méri a két klaszter közötti távolságot., Példaként az átlagos kapcsolatot használjuk, amely meghatározza a két klaszter közötti távolságot, hogy az első klaszter adatpontjai és a második klaszter adatpontjai közötti átlagos távolság legyen.
2. minden iteráción két klasztert egyesítünk egybe. A kombinálandó két klasztert a legkisebb átlagos kapcsolattal rendelkező klaszterek választják ki. I. e a kiválasztott távolságmérőnk szerint ez a két klaszter a legkisebb távolságra van egymástól, ezért a leginkább hasonlóak, ezért kombinálni kell.
3. a 2. lépést addig ismételjük, amíg el nem érjük a fa gyökerét i.,e csak egy Klaszterünk van, amely tartalmazza az összes adatpontot. Ily módon kiválaszthatjuk, hogy hány klasztert akarunk a végén, egyszerűen úgy, hogy kiválasztjuk, mikor kell abbahagyni a klaszterek kombinálását, azaz amikor abbahagyjuk a fa építését!

A hierarchikus klaszterezés nem követeli meg a klaszterek számának meghatározását, sőt azt is kiválaszthatjuk, hogy melyik klaszterek száma néz ki a legjobban, mivel fát építünk. Továbbá, az algoritmus nem érzékeny a választott távolság metrikus; mindegyik hajlamosak egyformán jól működik, míg más klaszterezési algoritmusok, a választott távolság metrikus kritikus., A hierarchikus klaszterezési módszerek különösen jó felhasználási esete az, amikor a mögöttes adatok hierarchikus struktúrával rendelkeznek, és a hierarchiát vissza kívánja állítani; más klaszterezési algoritmusok ezt nem tudják megtenni. A hierarchikus klaszterezés ezen előnyei alacsonyabb hatékonysággal járnak, mivel az O(n3) idő összetettsége, ellentétben a K-eszközök és a GMM lineáris összetettségével.