disztribúciók
a Dirac delta és hasonló
matematikai objektumok problémáinak középpontjában a differenciálhatóság problémája áll. Amint Dirac a fenti idézetben kijelentette, nem igazán kerül bajba, ha a δ funkcióját szimbolikus szabályként használja arra, hogy hogyan hat más funkciókra; azonban számításai során megkülönbözteti δ-t, és itt kezdődnek a problémák., Honnan lehet tudni a priori “amikor ezek a műveletek megengedettek”, amikor az embernek még nincs határozott meghatározása az objektumokról, vagy mit jelentene megkülönböztetni őket? Látni fogjuk, hogy ezek a kérdések hogyan vezetnek új, szigorúan meghatározott matematikai objektumok levezetéséhez.
Functionals
fontolja meg, hogy az egyik általában meghatározza a függvény származékát (vagy antiderivatíváját). Normál körülmények között, a “klasszikus” funkciók, van egy jól meghatározott szabály, amely leírja, hogy egy függvény térképek egy sor valós számok egy másik készlet, mondjuk f: ℝ →ℝ., Tekintettel erre, valamint az integrál vagy származék definícióira, egyértelműen meg lehet vizsgálni azokat az értékeket, amelyeket ezek az operátorok a függvényre alkalmazva adnak. Δ esetén nincs működőképes meghatározásunk ezen vonalak mentén. Ehelyett a gyakorlatban a δ-t leginkább az határozza meg, hogy hogyan működik más, jól meghatározott funkciókon (mint a (3)). Ez a legfontosabb betekintés, amely a disztribúciók modern elméletéhez vezet. Kiderül, hogy a helyes módja annak, hogy matematikailag kezelni δ, valamint egy nagy osztály hasonló tárgyak, hogy ne próbálja meghatározni őket, mint a funkciók egyáltalán., Ez a sor azt hittem, jól leírható Jean Dieudonne felülvizsgálata során (lásd ):
… egy kezdődik egy család nagyon “rendszeres” funkciók (általában
a tekintetben, hogy a megkülönböztető tulajdonságok), amelyek megfelelnek bizonyos (általában
szerves) kapcsolatok, illetve amelyek bizonyos műveletek lehetséges; s
aztán egy felfedezi, hogy egy a priori nagyobb családi funkciók megfelel
ugyanaz a kapcsolatok, vagy lehet kitéve hasonló műveletek. Sok
kérdést természetesen fel lehet tenni: valóban különbözik-e ez az új család
az elsőtől?, Ha igen, milyen a viszony a
két család között, és lehet-e pontos leírást adni az újról?
csak az “őstörténet” utolsó szakaszában jelenik meg az, amit
forradalmi szempontnak nevezhetünk, azzal a gondolattal, hogy
az “új család” a függvényektől eltérő tárgyakból állhat.
a többi, funkcionálisnak nevezett objektum. Gondolhat egy funkcionális
függvényként., Mivel a függvény egy egyedi leképezés a
számok egyik halmazából a másikba, a funkcionális F definiálható F leképezésként: C →ℝ,
ahol C néhány függvénykészlet. Vagyis a funkcionális térképek valós
számokra működnek., Egy egyszerű példa a funkcionális ez a típus a határozott integrál:

ami egyértelműen vesz egy f függvény egy sor megfelelő integrable funkciók, valamint térképek, hogy egy valós szám, értéke a szerves, vagy a görbe alatti terület f(x) között, valamint b. Ez csak egyetlen példa., El lehet képzelni végtelen számú functionals, és a halmazok functionals; az ember még tovább általánosítani és definiálni leképezések halmazok functionals valós számok. Ez sem itt, sem ott. Fontos, hogy a funkcionális koncepció felhasználható az eloszlások meghatározására.
A Tesztfunkciók halmaza
a cél elérése érdekében még egy meghatározásra van szükségünk. Ez azt jelenti, hogy megadja a függvénykészlet C értékét, amelyből a disztribúciók a függvényeket valós számokra térképezik., A függvényeket gyakran olyan halmazokban gyűjtik össze, amelyek meghatározzák a folytonosság mértékét, a differenciálhatóságot és származékaik folytonosságát. Azt mondjuk, hogy az f függvény a c⁰ készletben van (F ∈ c⁰ írása), ha az egész valós vonalon folyamatos abban az értelemben, hogy a határ minden ponton ugyanaz, ha balról vagy jobbról veszik; nem feltétlenül differenciálható. Azt mondjuk, hogy f ∈ C1, ha a származéka létezik és folyamatos, azaz F ‘ ∈ C⁰. Például a g(x) = |x| függvény folyamatos, de nem differenciálható x= 0; g C⁰-ban van, de nem C1-ben., Ezt általánosíthatjuk, és azt mondhatjuk, hogy a Cⁿ azon függvények halmaza, amelyek a folytonos függvények első n-származékait tartalmazzák, ahol n egész szám.
ahogy n nagyobb lesz, a készletek bizonyos értelemben “kisebbek”; mindig talál funkciókat (végtelenül sok!) cⁿ, de nem cⁿ ⁺ 1. Ezek a “folytonossági terek” tehát beágyazott részhalmazok sorozatát alkotják, az alábbiak szerint.

a funkciók végtelen sorozatának alja közelében találjuk a
ami természetesen az összes olyan függvény halmaza, amely végtelenül sok folyamatos származékkal rendelkezik. Ez utóbbi osztályba számos jól ismert és barátságos függvény tartozik(pl. sin(x); cos (x); eˣ; minden polinom)., Ezeket a funkciókat “sima” vagy “jól viselkedő” – nek nevezik, mert a differenciálás működését annyi alkalommal lehet elvégezni, amennyit csak akar, gond nélkül. De bár ez a készlet minden bizonnyal végtelenül sok taggal rendelkezik, ritkák abban az értelemben, hogy a legtöbb funkció nem olyan jól viselkedik.
az eloszlások meghatározására alkalmas készlet ennél is kisebb
. További kritériumot igényel: hogy a funkciók kompakt Támogatással rendelkezzenek. Ez a technikai kifejezés egyszerűen azt jelenti, hogy egy függvénynek nem nulla értéke van egy véges tartományon belül, és ezen kívül egyenletesen nulla., Ezért használja a jelölés
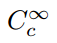
jelölésére a készlet végtelenül folyamatosan differenciálható függvények kompakt támogatás, illetve ilyen feladatok teszt funkciók. Annak érdekében, hogy meghatározzuk a funkcionálisok egy osztályát, amely ezt a készletet tartományként használja, biztosnak kell lennünk abban, hogy valóban vannak tagjai ennek a készletnek., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

A definíció
ettől a ponttól az eloszlás meghatározása egyszerű. Egy eloszlás egy lineáris funkcionális
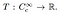
Ez, ez egy feltérképezése a vizsgált funkciók, hogy egy valós szám. Ahhoz hasonlóan, hogy egy adott függvény hogyan hat egy bemeneti számra, és hogyan hoz létre egy kimenetet, a specifikus eloszlásokat az határozza meg, hogy hogyan alakítják át a tesztfunkciókat számokká., A φ vizsgálati függvény eloszlása t (φ), vagy általában〈T,φ〉.
most már láthatjuk, hogy az eloszlásokat miért nevezik általánosított függvényeknek. Bármilyen
klasszikus funkciója, amely a szerves

jól meghatározott, megfelelő engedély, F olyan, hogy 〈F,φ〉ad az értéke ennek a szerves része., Vannak azonban olyan disztribúciók is, amelyek nem felelnek meg a klasszikus funkcióknak; az eloszlások általánosabbak. Amint már világosnak kell lennie, a klasszikus függvénynek nem megfelelő eloszlás kanonikus példája a Dirac δ., Ezért mi végre érkezik egy teljesen szigorú definíciója δ, mint a elrendezése olyan, hogy

A Generalizált vagy “Gyenge” Származékos
A δ engedély csak egy a végtelen sok disztribúció, amely nem
felel meg a klasszikus funkcióit. Ezek közül még néhányat meg tudunk szerezni azáltal, hogy megkülönböztetjük a δ-t az eloszlások értelmében., De hogyan oldja meg a
disztribúció fogalma a differenciálás problémáját, amint azt korábban tárgyaltuk? A disztribúciókra való alkalmazáshoz csak a differenciálás fogalmát kell általánosítani.
fontolja meg az f ∈ C1 függvényt, hogy folyamatosan differenciálható legyen. Kiszámításához használja integrálással, azt látjuk, hogy

Az a kifejezés, hogy a zárójelben eltűnik, mivel φ, mint egy teszt funkció, van kompakt támogatást., Ez generalizes, hogy egy engedély, mondjuk F’, a funkciónak megfelelő f’:

Ez a számítás generalizes elég könnyen disztribúció, amely nem felel meg a klasszikus f függvény., Ilyen módon meg tudjuk határozni a származékos T T T abban az értelemben, disztribúciók:

Ez is nevezik a gyenge származék, mivel kiterjed származékok, hogy a funkciókat, amelyek rendszerint nem differenciálható. Ez még tovább általánosítja a magasabb rendű származékokat., Határozhatunk meg, az n-edik deriváltja egy forgalmazás T T⁽ⁿ⁾, amennyiben az utóbbi a elrendezése olyan, hogy

Itt
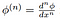
a klasszikus származéka a teszt funkció, ami biztos,
hogy létezik az a meghatározás, teszt funkciók!, Ebből következik, hogy minden disztribúció végtelenül differenciálható (az eloszlások értelmében).
Ez teljesen eltávolítja azt a küzdelmet, amellyel Dirac és mások szembesültek a δ függvény differenciálásakor. Amit itt definiáltunk, a δ származéka egyszerűen egy másik függvény deriváltjának értékét nullára emeli., Hivatalosan,

Ez biztosítja a szigorú matematikai keretet a származékos δ, hogy megjelent az irodalomban jóval azelőtt, hogy ez az elmélet jött létre.
számos más olyan művelet is létezik, amelyek a disztribúciókra általánosított függvényekre vonatkoznak. Ezek hozzáadhatók és kivonhatók, konvolválhatók és átalakíthatók Laplace és Fourier transzformációk segítségével., Azonban lehetetlen meghatározni az eloszlások sokszorozódását oly módon, hogy megőrizze a klasszikus függvényekre vonatkozó algebrát (a Schwartz Lehetetlenségi tétel).