LEONARDO FIBONACCI – OLASZ MATEMATIKUS (ÍRTA LEBER ABACI)

Leonardo Pisa (Fibonacci) (c.1170-1250)

A 13 Században olasz Leonardo a Pisa által jobban ismert a beceneve, Fibonacci, talán a legtehetségesebb Nyugati matematikus a Középkorban. Életéről keveset tudunk, csak annyit, hogy Vámos fia volt, és gyermekként apjával Észak-Afrikát járta, ahol Arab matematikát tanult., Itáliába való visszatérésekor segített e tudás terjesztésében Európa-szerte, így elindítva az európai matematika megújulását, amely évszázadok óta nagyrészt nyugvó volt a sötét középkorban.

különösen 1202-ben írt egy rendkívül befolyásos könyvet “Liber Abaci” (“számítási könyv”) néven, amelyben elősegítette a Hindu-arab számrendszer használatát, leírva annak számos előnyét a kereskedők és a matematikusok számára egyaránt a római számok ügyetlen rendszerével szemben, majd Európában használják., Nyilvánvaló előnyei ellenére a rendszer elterjedése Európában lassú volt (ez végül is az iszlám elleni keresztes hadjáratok idején volt, amikor valami arabot nagy gyanúval néztek meg), és az arab számokat 1299-ben Firenze városában is betiltották azzal az ürüggyel, hogy könnyebben hamisíthatók, mint a római számok. A józan ész azonban végül érvényesült, és az új rendszert a 15.században egész Európában elfogadták, így a Római rendszer elavult., Ebben a munkában először a frakciók vízszintes sáv jelölését is használták (bár az arab gyakorlatot követve a frakciót az egész szám bal oldalára helyezték).

Fibonacci-szekvencia

a híres Fibonacci-szekvencia felfedezése

Fibonacci a legismertebb, bár egy bizonyos számsorozat Európába való bevezetése miatt, amely azóta Fibonacci-számokként vagy Fibonacci-szekvenciaként vált ismertté., Felfedezte a szekvenciát – az Európában ismert első rekurzív számsorozatot -, miközben figyelembe vette a “Liber Abaci” gyakorlati problémáját, amely magában foglalja a nyulak hipotetikus populációjának növekedését idealizált feltételezések alapján. Megjegyezte, hogy minden havi generáció után a nyulak párjainak száma 1-ről 2-ről 3-ra 5-re 8-ra 13-ra stb. nőtt, és azonosította a sorrend előrehaladását az előző két kifejezés hozzáadásával (matematikai értelemben Fn = Fn-1 + Fn-2), egy olyan szekvencia, amely elméletileg határozatlan időre meghosszabbítható.,

A sorozatot, amely tulajdonképpen már ismert Indiai matematikusok, mivel a 6., számos érdekes matematikai tulajdonságai, sokan pedig a következtetések, összefüggések, hogy a sorrend nem fedeztek fel, míg több évszázados után Fibonacci halála., Például, a sorrend regenerálódik, néhány meglepő módon: minden harmadik F-szám osztható 2 (F3 = 2), minden negyedik F-szám osztható 3-mal (F4 = 3), minden ötödik F-szám osztható 5 (F5 = 5), minden hatodik F-szám osztható 8 (F6 = 8), minden hetedik F-szám osztható 13 (F7 = 13), stb., A szekvencia számait a természetben is mindenütt jelen vannak: többek között a virágos növények számos fajának szirmai vannak a Fibonacci-sorrendben; az ananász spirális elrendezése az 5S és 8s-ben, a 8s és 13S pinekonoké, a napraforgófejek magjai pedig a 21S, 34s, 55s vagy még magasabb sorrendben; stb.,

Az aranymetszés φ

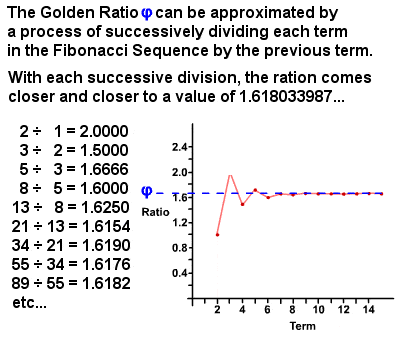
Az aranymetszés φ származtatható a Fibonacci-Sorozat

a 1750s, Robert Simson kell jegyezni, hogy ez az arány minden kifejezés a Fibonacci-Sorozat a korábbi távú megközelítés, a még nagyobb pontosság magasabb a feltételek, arány körülbelül 1 : 1.6180339887 (ez valójában egy irracionális szám, egyenlő (1 + √5)⁄2, amely azóta is számított, hogy több ezer tizedesjegyre kerekítve)., Ezt az értéket arany aránynak nevezik, más néven arany Középértéknek, Aranymetszésnek, isteni aránynak stb., és általában a görög Phi φ betűvel (vagy néha a nagybetűvel Phi Φ) jelölik. Alapvetően két mennyiség van az Aranyarányban, ha a mennyiségek összegének a nagyobb mennyiséghez viszonyított aránya megegyezik a nagyobb mennyiség és a kisebb arányával. Maga az Aranyarány számos egyedi tulajdonsággal rendelkezik, mint például 1⁄φ = φ – 1 (0.618…) és φ2 = φ + 1 (2.618…), és számtalan példa található rá mind a természetben, mind az emberi világban.,

A téglalap oldalai arány 1 : φ ismert, mint egy Arany Téglalapot, sok művészek, építészek a történelem során (nyúlik vissza, az ókori Egyiptomban, Görögországban, de különösen népszerű a Reneszánsz művészet Leonardo da Vinci, valamint kortársai) rendelkezik arányos, a munkálatok körülbelül segítségével az aranymetszés, illetve Arany Négyszögek, amelyek széles körben tekinthető, alapvetően esztétikus. Az egyre kisebb beágyazott arany téglalapok ellentétes pontjait összekötő ív logaritmikus spirált képez, amelyet Arany spirálnak neveznek., Az Aranyarány és az arany spirál a természetben meglepő számú esetben is megtalálható, a kagylóktól a virágokig az állati szarvakig az emberi testekig a viharrendszerekig a teljes galaxisokig.,

nem szabad elfelejteni azonban, hogy a Fibonacci-Sorozat volt, igazából csak egy nagyon apró elem a “Liber Abaci” – sőt, a sorozat egyetlen kapott Fibonacci neve 1877-ben, amikor Eduouard Lucas úgy döntött, hogy fizessék meg neki, hogy megnevezi a sorozat után, ő pedig, hogy a Fibonacci-maga nem volt felelős annak, hogy egy érdekes matematikai tulajdonságai a sorrend, a kapcsolat az Arany középút Arany Téglalapok pedig Spirál, stb.,

Rács Szorzás

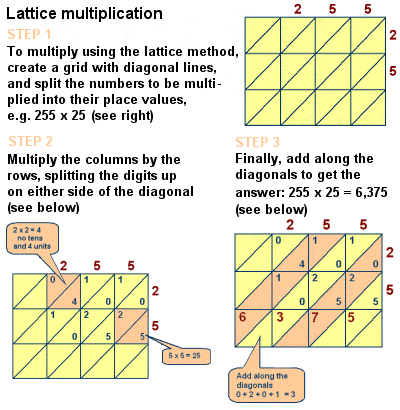
Fibonacci bevezetett rács szorzás, hogy Európa

Azonban a könyv hatása a középkori matematika tagadhatatlan, de ez nem is tartalmaznia viták számos más matematikai problémák, mint például a Kínai Többi Tétel, tökéletes számok, prímszám, a képletek számtani sorozat, négyzetes piramis számok, Euklideszi geometriai bizonyítások, meg egy tanulmány a szimultán lineáris egyenletek mentén Diophantosz Al-Karaji., Leírta a nagy számok megszorzásának rácsos (vagy szita) szorzási módszerét is, egy módszert – amelyet eredetileg az Iszlám matematikusok, például az Al-Khwarizmi úttörője – algoritmikusan egyenértékű a hosszú szorzással.

sem” Liber Abaci ” Fibonacci egyetlen könyve, bár ez volt a legfontosabb., A “Liber Quadratorum” (“A Könyv a Négyzetek”), például egy könyv algebra, megjelent 1225-ben, amely úgy tűnik, egy nyilatkozat, amit most az úgynevezett Fibonacci személyazonosságát – néha úgy is ismert, mint Brahmagupta személyazonosságát után a sokkal korábbi Indiai matematikus, aki szintén ugyanerre a következtetésre jutottam, hogy a termék a két összeget, két négyzet maga összege két négyzet pl. (12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,