Distribuzioni
Il problema principale al centro dei problemi con il delta di Dirac e simili
oggetti matematici è il problema della differenziabilità. Come Dirac ha dichiarato nella citazione sopra, non si corre davvero nei guai se si usa la sua funzione δ come regola simbolica per come agisce su altre funzioni; tuttavia, procede a differenziare δ nei suoi calcoli, ed è qui che i problemi iniziano davvero., Come si può sapere a priori “quando queste operazioni sono consentite” quando non si ha nemmeno una definizione ferma degli oggetti, o cosa significherebbe differenziarli? Vedremo come queste domande portano alla derivazione di oggetti matematici nuovi e rigorosamente definiti.
Funzionali
Considera come normalmente si determina la derivata (o antiderivativa) di una funzione. In circostanze normali, con le funzioni “classiche”, hai una regola ben definita che descrive come una funzione mappa un insieme di numeri reali a un altro insieme, ad esempio f: → → ℝ., Dato questo e le definizioni dell’integrale o della derivata, si può quindi indagare chiaramente i valori che questi operatori producono quando applicati alla funzione. Nel caso di δ, non abbiamo una definizione praticabile per procedere su queste linee. Invece, in pratica δ è definito in modo più prominente dal modo in cui opera su altre funzioni ben definite (come in (3)). Questa è l’intuizione chiave che porta alla moderna teoria delle distribuzioni. Si scopre che il modo corretto per trattare matematicamente δ, e una grande classe di oggetti simili, è smettere di cercare di definirli come funzioni., Questa linea di pensiero è ben descritto da Jean Dieudonne, nella sua recensione (vedi ):
… si inizia con una famiglia molto “normali” funzioni (di solito con un
rispetto a un differenziale di proprietà), che soddisfano alcuni (in genere
integrale) relazioni, o di talune operazioni sono possibili; e
poi si scopre che un a priori grande famiglia di funzioni soddisfa
le stesse relazioni, o può essere sottoposto a operazioni simili. Molte
domande allora possono naturalmente essere chiesto: È questa nuova famiglia davvero
diverso dal primo?, Se lo è, quali sono le relazioni tra le due famiglie, e si può dare una descrizione precisa di quella nuova?
È solo nell’ultima fase della “preistoria” che emergerà quello che potrebbe essere
definito un punto di vista rivoluzionario, con l’idea che
la “nuova famiglia” potrebbe consistere in oggetti diversi dalle funzioni.
Gli altri oggetti a cui si allude sono funzionali. Puoi pensare a un funzionale
come una funzione di funzioni., Poiché una funzione è una mappatura univoca da un insieme di numeri
a un altro, una F funzionale può essere definita come una mappatura F : C →ℝ,
dove C è un insieme di funzioni. Cioè, una mappa funzionale funziona con numeri reali
., Un semplice esempio di un funzionale di questo tipo è l’integrale definito:

che è chiaramente una funzione f da un insieme di persone integrabili funzioni e le mappe è un numero reale, il valore dell’integrale, o l’area sotto la curva f(x) tra a e b. Questo è solo un singolo esempio., Si può immaginare un numero infinito di funzionali e insiemi di funzionali; si potrebbe anche continuare a generalizzare e definire mappature da insiemi di funzionali a numeri reali. Questo non è né qui né là. Ciò che è importante è che il concetto funzionale può essere utilizzato per definire le distribuzioni.
L’insieme delle funzioni di test
Abbiamo bisogno di un’altra definizione per raggiungere il nostro obiettivo. Ciò equivale a specificare il set C di funzioni da cui le distribuzioni mapperanno le funzioni a numeri reali., Le funzioni sono spesso raccolte in insiemi che specificano il loro grado di continuità, differenziabilità e continuità delle loro derivate. Diciamo che una funzione f è nell’insieme C C (scrivi f C c.) se è continua su tutta la linea reale nel senso che il limite in tutti i punti è lo stesso se preso da sinistra o da destra; non è necessariamente differenziabile. Diciamo che f C C1 se la sua derivata esiste ed è continua, cioè f ‘ C C.. Ad esempio, la funzione g(x) = |x| è continua ma non differenziabile a x= 0; g è in C but ma non in C1., Possiamo generalizzare questo e dire che cⁿ è l’insieme di funzioni che hanno per le funzioni continue le loro prime n derivate, dove n è un numero intero.
Quando n diventa più grande, i set diventano in un certo senso “più piccoli;” puoi sempre trovare funzioni (infinitamente molte!) che sono in C but ma non c C 1. Questi “spazi di continuità” formano quindi una sequenza di sottoinsiemi nidificati, come illustrato di seguito.

Vicino alla parte inferiore di questa sequenza infinita di insiemi di funzioni troviamo il set
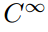
che è, naturalmente, l’insieme di tutte le funzioni che hanno un numero infinito continuo derivati. Molte funzioni ben note e amichevoli sono in quest’ultima classe(ad esempio sin(x); cos (x); eˣ; tutti i polinomi)., Queste funzioni sono chiamate “lisce” o” ben educate ” perché si può eseguire l’operazione di differenziazione su di esse tutte le volte che si vuole senza cura. Ma mentre questo set ha certamente infinitamente molti membri, sono rari nel senso che la maggior parte delle funzioni non sono così ben educati.
L’insieme che è adatto per la definizione di distribuzioni è ancora più piccolo
di questo. Richiede un criterio aggiuntivo: che le funzioni abbiano un supporto compatto. Questo termine tecnico significa semplicemente che una funzione ha valori diversi da zero all’interno di un dominio finito ed è uniformemente zero al di fuori di questo., Abbiamo quindi utilizzare la notazione
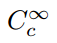
per indicare l’insieme di infinitamente continuamente differenziabile funzioni a supporto compatto, e chiamare tali funzioni le funzioni di test. Per definire una classe di funzionali usando questo set come dominio, dovremmo essere sicuri che ci siano effettivamente membri di questo set., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

La Definizione
Da questo punto la definizione di una distribuzione è semplice. Una distribuzione è un funzionale lineare
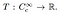
Che è, si tratta di una mappatura dal set di funzioni di prova per un numero reale. Analogamente a come una funzione specifica agisce su un numero di input e produce un output, le distribuzioni specifiche sono definite dal modo in cui trasformano le funzioni di test in numeri., L’azione di distribuzione della funzione di prova φ può essere scritta come T (φ), o comunemente come T T, φ〉.
Ora si può vedere perché le distribuzioni sono chiamate funzioni generalizzate. Per qualsiasi
classica funzione per cui l’integrale

è ben definito, non c’è una corrispondente distribuzione di F tale che 〈F,f〉, fornisce il valore di questo integrale., Tuttavia, ci sono anche distribuzioni che non corrispondono alle funzioni classiche; le distribuzioni sono più generali. Come dovrebbe essere chiaro ormai, l’esempio canonico di una distribuzione che non corrisponde a una funzione classica è il Dirac δ., Abbiamo quindi finalmente arrivare ad una cucina completamente una definizione rigorosa di δ come la distribuzione tale che

La Generalizzata o “Debole” Derivati
La distribuzione δ è solo una delle infinite distribuzioni che non
corrispondono alle classiche funzioni. Possiamo ottenere alcuni di questi differenziando δ nel senso delle distribuzioni., Ma in che modo il concetto di distribuzione risolve il problema della differenziazione come discusso in precedenza? Dobbiamo solo generalizzare il concetto di differenziazione da applicare alle distribuzioni.
Considera una funzione f C C1, in modo che sia continuamente differenziabile. Calcolo utilizzando integrazione per parti, vediamo che

Il termine tra parentesi quadre svanisce dal φ, come una funzione di test, ha supporto compatto., Questo si estende per una distribuzione, dire che F’, corrispondente alla funzione f’:

Questo calcolo si estende facilmente per le distribuzioni che non corrispondono ad una classica funzione f., In questo modo, siamo in grado di definire la derivata di T’ T nel senso delle distribuzioni:

Questo è anche a volte indicato come il debole derivati, dal momento che si estende derivati di funzioni che normalmente non sarebbe una funzione derivabile. Questo generalizza ancora di più, ai derivati di ordine superiore., Possiamo definire l’ennesimo derivata di una distribuzione T T⁽ü⁾, dove quest’ultima è la distribuzione tale che

Qui
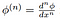
è la classica derivata della funzione di test quale è assicurata
a esistere per la definizione stessa di funzioni di test!, Ne consegue che tutte le distribuzioni sono infinitamente differenziabili (nel senso di distribuzioni).
Questo rimuove completamente la lotta che Dirac e altri hanno affrontato quando hanno differenziato la funzione δ. Da quello che abbiamo definito qui, una derivata di δ semplicemente setaccia per il valore di un’altra derivata di funzioni a zero., Formalmente,

Questo fornisce un rigoroso quadro matematico per i derivati di δ che è apparso in letteratura a lungo prima di questa teoria è entrato in esistenza.
Ci sono un certo numero di altre operazioni che si applicano a funzioni che sono state generalizzate per applicarsi alle distribuzioni. Possono essere aggiunti e sottratti, convolti e trasformati usando trasformazioni di Laplace e Fourier., Tuttavia, è impossibile definire la moltiplicazione delle distribuzioni in un modo che preservi l’algebra che si applica alle funzioni classiche (il Teorema dell’Impossibilità di Schwartz).