I 5 algoritmi di clustering Gli scienziati dei dati hanno bisogno di sapere

Recentemente ho iniziato una newsletter educativa incentrata sul libro. Book Dives è una newsletter bisettimanale in cui per ogni nuovo numero ci immergiamo in un libro di saggistica. Imparerai a conoscere le lezioni principali del libro e come applicarle nella vita reale. Puoi iscriverti qui.

Il clustering è una tecnica di apprendimento automatico che prevede il raggruppamento di punti dati. Dato un insieme di punti dati, possiamo utilizzare un algoritmo di clustering per classificare ogni punto dati in un gruppo specifico., In teoria, i punti dati che si trovano nello stesso gruppo dovrebbero avere proprietà e/o caratteristiche simili, mentre i punti dati in gruppi diversi dovrebbero avere proprietà e/o caratteristiche altamente dissimili. Il clustering è un metodo di apprendimento non supervisionato ed è una tecnica comune per l’analisi statistica dei dati utilizzata in molti campi.

Nella scienza dei dati, possiamo utilizzare l’analisi di clustering per ottenere alcune preziose informazioni dai nostri dati vedendo in quali gruppi rientrano i punti dati quando applichiamo un algoritmo di clustering., Oggi, stiamo andando a guardare 5 algoritmi di clustering popolari che gli scienziati di dati hanno bisogno di conoscere e dei loro pro e contro!

K-Means Clustering

K-Means è probabilmente l’algoritmo di clustering più noto. Viene insegnato in molte lezioni introduttive di scienza dei dati e apprendimento automatico. È facile da capire e implementare nel codice! Controlla il grafico qui sotto per un’illustrazione.,

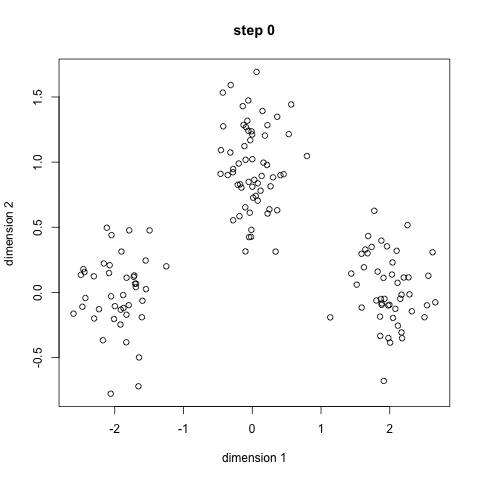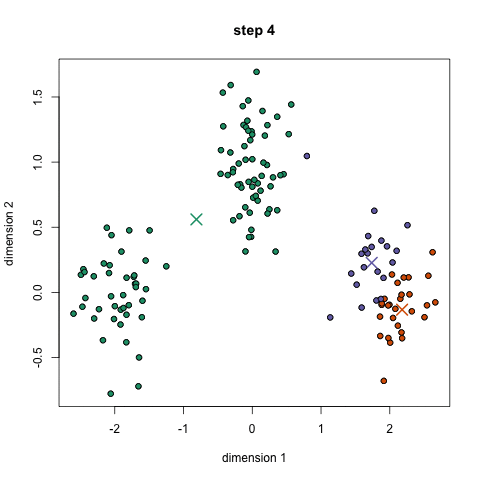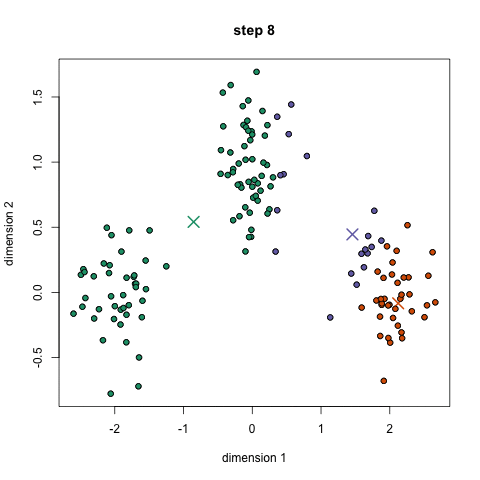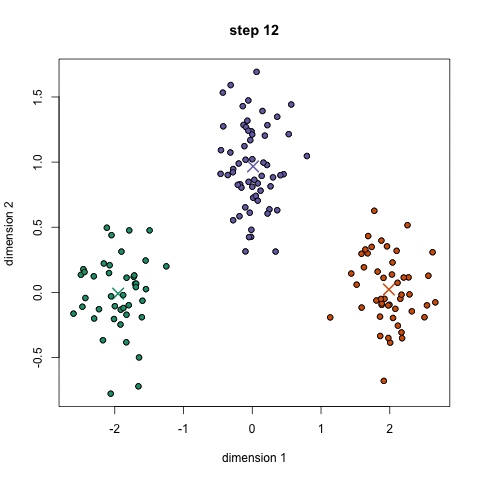
1. Per iniziare, dobbiamo prima selezionare un numero di classi/gruppi di utilizzare in modo casuale e inizializzare i loro rispettivi punti centrali. Per capire il numero di classi da utilizzare, è bene dare una rapida occhiata ai dati e cercare di identificare eventuali raggruppamenti distinti. I punti centrali sono vettori della stessa lunghezza di ciascun vettore di punti dati e sono le ” X ” nel grafico sopra.,
2. Ogni punto dati viene classificato calcolando la distanza tra quel punto e ogni centro del gruppo e quindi classificando il punto nel gruppo il cui centro è più vicino ad esso.
3. In base a questi punti classificati, ricalcoliamo il centro del gruppo prendendo la media di tutti i vettori del gruppo.
4. Ripetere questi passaggi per un determinato numero di iterazioni o fino a quando i centri di gruppo non cambiano molto tra le iterazioni. Si può anche scegliere di inizializzare in modo casuale i centri di gruppo un paio di volte, e quindi selezionare l’esecuzione che sembra che ha fornito i migliori risultati.,

K-Means ha il vantaggio di essere piuttosto veloce, poiché tutto ciò che stiamo facendo è calcolare le distanze tra punti e centri di gruppo; pochissimi calcoli! Ha quindi una complessità lineare O (n).

D’altra parte, K-Means ha un paio di svantaggi. In primo luogo, devi selezionare quanti gruppi/classi ci sono. Questo non è sempre banale e idealmente con un algoritmo di clustering vorremmo che li capisse per noi perché il punto è ottenere qualche intuizione dai dati., K-means inizia anche con una scelta casuale di centri di cluster e quindi può produrre diversi risultati di clustering su diverse esecuzioni dell’algoritmo. Pertanto, i risultati potrebbero non essere ripetibili e mancare di coerenza. Altri metodi di cluster sono più coerenti.

K-Medians è un altro algoritmo di clustering relativo a K-Means, tranne che invece di ricalcolare i punti centrali del gruppo usando la media usiamo il vettore mediano del gruppo., Questo metodo è meno sensibile ai valori anomali (a causa dell’utilizzo della Mediana) ma è molto più lento per set di dati più grandi poiché l’ordinamento è richiesto su ogni iterazione quando si calcola il vettore mediano.

Mean-Shift Clustering

Mean shift clustering è un algoritmo basato su finestre scorrevoli che tenta di trovare aree dense di punti dati. Si tratta di un algoritmo basato centroide significa che l’obiettivo è quello di individuare i punti centrali di ogni gruppo/classe, che funziona aggiornando i candidati per i punti centrali per essere la media dei punti all’interno della finestra scorrevole., Queste finestre candidate vengono quindi filtrate in una fase di post-elaborazione per eliminare i quasi duplicati, formando l’insieme finale di punti centrali e i loro gruppi corrispondenti. Controlla il grafico qui sotto per un’illustrazione.

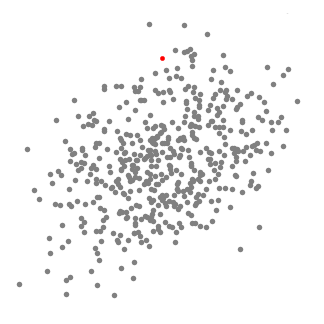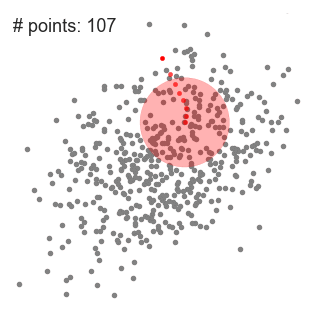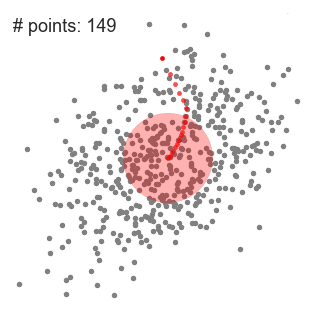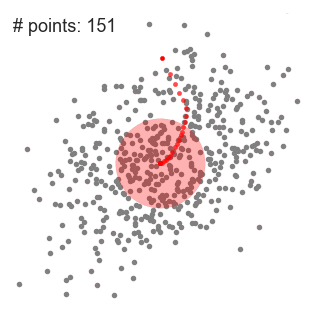
1. Per spiegare mean-shift consideriamo un insieme di punti dello spazio a due dimensioni come l’illustrazione di cui sopra., Iniziamo con una finestra scorrevole circolare centrata in un punto C (selezionato casualmente) e con raggio r come kernel. Mean shift è un algoritmo di salita che comporta lo spostamento iterativo di questo kernel in una regione a densità più elevata su ogni passaggio fino alla convergenza.
2. Ad ogni iterazione, la finestra scorrevole viene spostata verso regioni di maggiore densità spostando il punto centrale alla media dei punti all’interno della finestra (da cui il nome). La densità all’interno della finestra scorrevole è proporzionale al numero di punti al suo interno., Naturalmente, passando alla media dei punti nella finestra si sposterà gradualmente verso aree di maggiore densità di punti.
3. Continuiamo a spostare la finestra scorrevole in base alla media fino a quando non c’è una direzione in cui uno spostamento può ospitare più punti all’interno del kernel. Controlla il grafico sopra; continuiamo a spostare il cerchio fino a quando non aumentiamo più la densità (cioè il numero di punti nella finestra).
4. Questo processo di passaggi da 1 a 3 viene eseguito con molte finestre scorrevoli fino a quando tutti i punti si trovano all’interno di una finestra., Quando più finestre scorrevoli si sovrappongono, la finestra contenente il maggior numero di punti viene mantenuta. I punti dati vengono quindi raggruppati in base alla finestra scorrevole in cui risiedono.

Un’illustrazione dell’intero processo da un capo all’altro con tutte le finestre scorrevoli è mostrata di seguito. Ogni punto nero rappresenta il centroide di una finestra scorrevole e ogni punto grigio è un punto dati.,

In contrasto con K-means clustering, non è necessario selezionare il numero di cluster come mean-shift rileva automaticamente questa. Questo è un enorme vantaggio. Il fatto che i centri del cluster convergano verso i punti di massima densità è anche abbastanza desiderabile in quanto è abbastanza intuitivo da capire e si adatta bene in un senso naturalmente basato sui dati., Lo svantaggio è che la selezione della dimensione/raggio della finestra “r” può essere non banale.

Clustering spaziale basato sulla densità di applicazioni con rumore (DBSCAN)

DBSCAN è un algoritmo cluster basato sulla densità simile a mean-shift, ma con un paio di vantaggi notevoli. Scopri un altro grafico di fantasia qui sotto e cominciamo!,

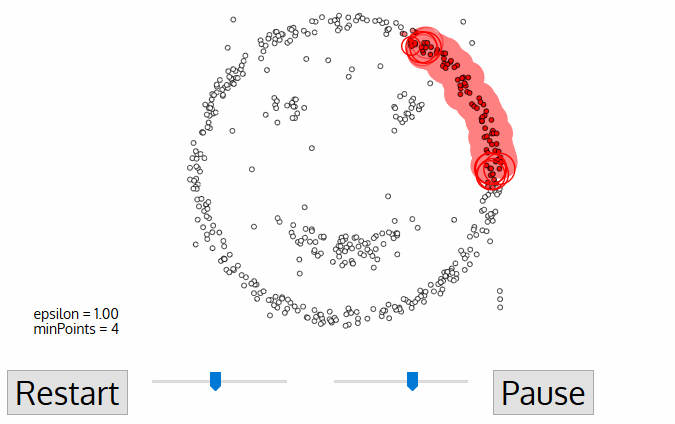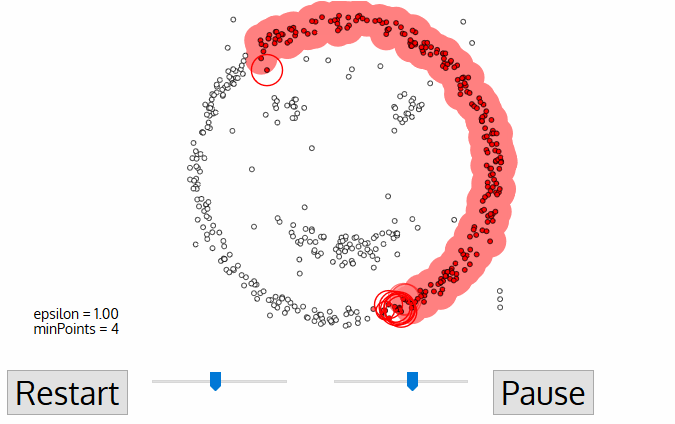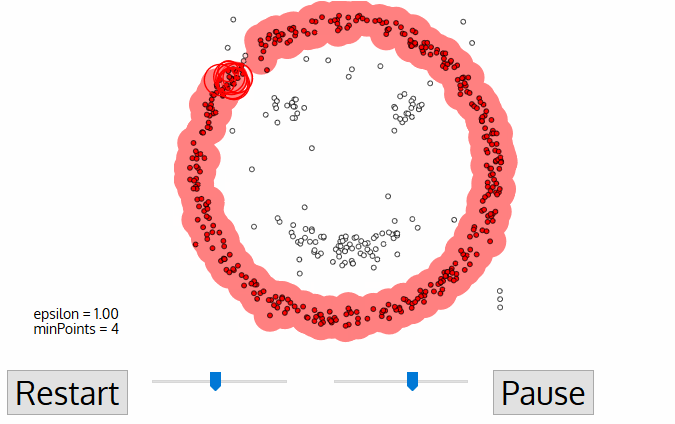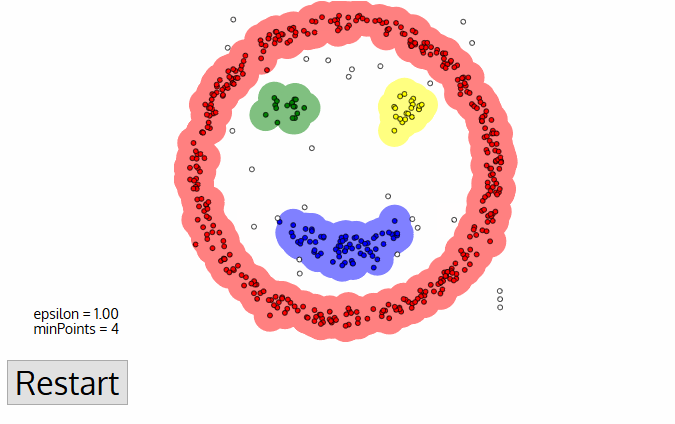
1. DBSCAN inizia con un numero arbitrario di dati di partenza punto che non ha ancora visitato. Il vicinato di questo punto viene estratto usando una distanza epsilon ε (Tutti i punti che si trovano all’interno della distanza ε sono punti di vicinato).,
2. Se c’è un numero sufficiente di punti (secondo minPoints) all’interno di questo quartiere, il processo di clustering inizia e il punto dati corrente diventa il primo punto nel nuovo cluster. In caso contrario, il punto verrà etichettato come rumore (in seguito questo punto rumoroso potrebbe diventare la parte del cluster). In entrambi i casi quel punto è contrassegnato come “visitato”.
3. Per questo primo punto nel nuovo cluster, anche i punti all’interno del suo quartiere di distanza ε diventano parte dello stesso cluster., Questa procedura di fare tutti i punti nel quartiere ε appartengono allo stesso cluster viene quindi ripetuta per tutti i nuovi punti che sono stati appena aggiunti al gruppo di cluster.
4. Questo processo di passaggi 2 e 3 viene ripetuto fino a quando tutti i punti del cluster sono determinati cioè tutti i punti all’interno del quartiere ε del cluster sono stati visitati ed etichettati.
5. Una volta che abbiamo finito con il cluster corrente, un nuovo punto non visitato viene recuperato ed elaborato, portando alla scoperta di un ulteriore cluster o rumore. Questo processo si ripete fino a quando tutti i punti sono contrassegnati come visitati., Poiché alla fine di questo tutti i punti sono stati visitati, ogni punto sarà stato contrassegnato come appartenente a un cluster o come rumore.

DBSCAN presenta alcuni grandi vantaggi rispetto ad altri algoritmi di clustering. In primo luogo, non richiede affatto un numero di cluster impostato in pe. Identifica anche i valori anomali come rumori, a differenza di mean-shift che li getta semplicemente in un cluster anche se il punto dati è molto diverso. Inoltre, può trovare cluster di dimensioni arbitrarie e di forma arbitraria abbastanza bene.,

Lo svantaggio principale di DBSCAN è che non funziona come gli altri quando i cluster sono di densità variabile. Questo perché l’impostazione della soglia di distanza ε e minPoints per identificare i punti di vicinato varierà da cluster a cluster quando la densità varia. Questo inconveniente si verifica anche con dati molto dimensionali poiché ancora una volta la soglia di distanza ε diventa difficile da stimare.,

Clustering di Expectation–Maximization (EM) usando Gaussian Mixture Models (GMM)

Uno dei principali inconvenienti di K-Means è il suo uso ingenuo del valore medio per il centro del cluster. Possiamo capire perché questo non è il modo migliore di fare le cose guardando l’immagine qui sotto. Sul lato sinistro, sembra abbastanza ovvio all’occhio umano che ci sono due ammassi circolari con raggio diverso centrato alla stessa media. K-Means non può gestirlo perché i valori medi dei cluster sono molto vicini tra loro., K-Means fallisce anche nei casi in cui i cluster non sono circolari, sempre come risultato dell’uso della media come centro del cluster.

Gaussian mixture Models (Mgm) non ci darà più flessibilità rispetto a K-means. Con i GMM assumiamo che i punti dati siano distribuiti gaussiani; questa è un’ipotesi meno restrittiva rispetto a dire che sono circolari usando la media., In questo modo, abbiamo due parametri per descrivere la forma dei cluster: la media e la deviazione standard! Prendendo un esempio in due dimensioni, ciò significa che i cluster possono assumere qualsiasi tipo di forma ellittica (poiché abbiamo una deviazione standard in entrambe le direzioni x e y). Pertanto, ogni distribuzione gaussiana viene assegnata a un singolo cluster.

Per trovare i parametri della gaussiana per ogni cluster (ad esempio la media e la deviazione standard), useremo un algoritmo di ottimizzazione chiamato Expectation–Maximization (EM)., Dai un’occhiata al grafico qui sotto come illustrazione dei Gaussiani montati sui cluster. Quindi possiamo procedere con il processo di clustering di massimizzazione delle aspettative utilizzando GMM.

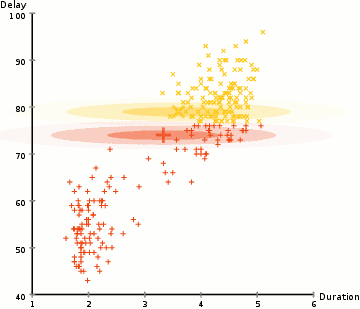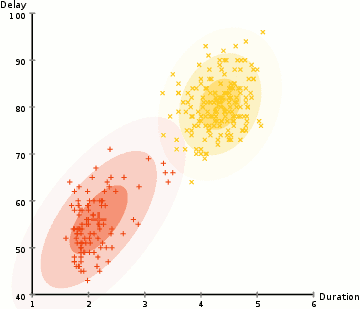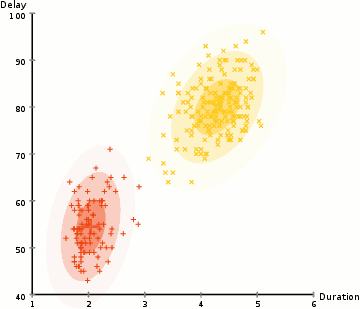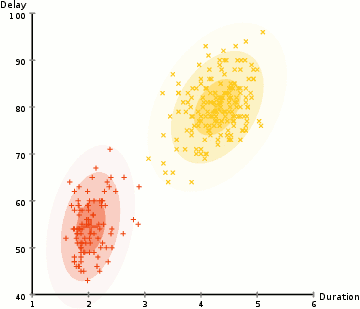
1. Iniziamo selezionando il numero di cluster (come K-Mezzo fa) e casualmente inizializzazione di una distribuzione Gaussiana parametri per ogni cluster., Si può provare a fornire una buona stima per i parametri iniziali dando una rapida occhiata anche ai dati. Anche se nota, come si può vedere nel grafico sopra, questo non è necessario al 100% in quanto i gaussiani iniziano a essere molto poveri ma sono rapidamente ottimizzati.
2. Date queste distribuzioni gaussiane per ciascun cluster, calcolare la probabilità che ogni punto dati appartenga a un particolare cluster. Più un punto è vicino al centro gaussiano, più è probabile che appartenga a quell’ammasso., Questo dovrebbe avere un senso intuitivo poiché con una distribuzione gaussiana supponiamo che la maggior parte dei dati si trovi più vicino al centro del cluster.
3. In base a queste probabilità, calcoliamo un nuovo set di parametri per le distribuzioni gaussiane in modo tale da massimizzare le probabilità dei punti dati all’interno dei cluster. Calcoliamo questi nuovi parametri usando una somma ponderata delle posizioni dei punti dati, dove i pesi sono le probabilità del punto dati appartenente a quel particolare cluster., Per spiegare questo visivamente possiamo dare un’occhiata al grafico sopra, in particolare il cluster giallo come esempio. La distribuzione inizia casualmente alla prima iterazione, ma possiamo vedere che la maggior parte dei punti gialli si trova a destra di quella distribuzione. Quando calcoliamo una somma ponderata per le probabilità, anche se ci sono alcuni punti vicino al centro, la maggior parte di essi si trova sulla destra. Così naturalmente la media della distribuzione è spostata più vicino a quelle serie di punti. Possiamo anche vedere che la maggior parte dei punti sono “in alto a destra in basso a sinistra”., Pertanto la deviazione standard cambia per creare un’ellisse più adatta a questi punti, per massimizzare la somma ponderata dalle probabilità.
4. I passaggi 2 e 3 vengono ripetuti iterativamente fino alla convergenza, dove le distribuzioni non cambiano molto da iterazione a iterazione.

Ci sono 2 vantaggi chiave per l’utilizzo di GMM. In primo luogo i GMM sono molto più flessibili in termini di covarianza dei cluster rispetto ai K-Means; a causa del parametro di deviazione standard, i cluster possono assumere qualsiasi forma di ellisse, piuttosto che essere limitati ai cerchi., K-Means è in realtà un caso speciale di GMM in cui la covarianza di ogni cluster lungo tutte le dimensioni si avvicina a 0. In secondo luogo, poiché i GMM utilizzano le probabilità, possono avere più cluster per punto dati. Quindi, se un punto dati si trova nel mezzo di due cluster sovrapposti, possiamo semplicemente definire la sua classe dicendo che appartiene X-percentuale alla classe 1 e Y-percentuale alla classe 2. I. e GMM supportano l’adesione mista.

Clustering gerarchico agglomerativo

Gli algoritmi di clustering gerarchico rientrano in 2 categorie: top-down o bottom-up., Gli algoritmi bottom-up trattano ogni punto dati come un singolo cluster all’inizio e poi successivamente uniscono (o agglomerano) coppie di cluster fino a quando tutti i cluster sono stati uniti in un singolo cluster che contiene tutti i punti dati. Il clustering gerarchico bottom-up è quindi chiamato clustering agglomerativo gerarchico o HAC. Questa gerarchia di cluster è rappresentata come un albero (o dendrogramma). La radice dell’albero è il cluster unico che raccoglie tutti i campioni, le foglie sono i cluster con un solo campione., Controllare il grafico di seguito un’illustrazione, prima di passare all’algoritmo passi

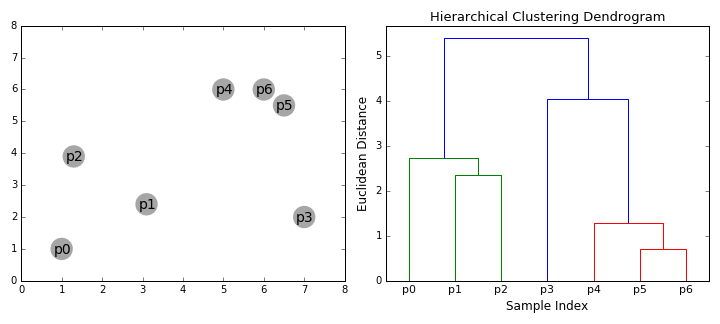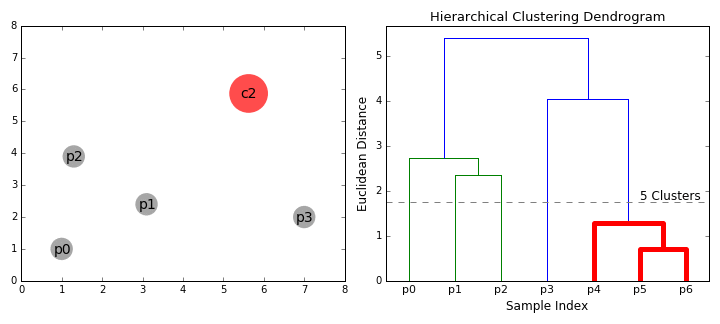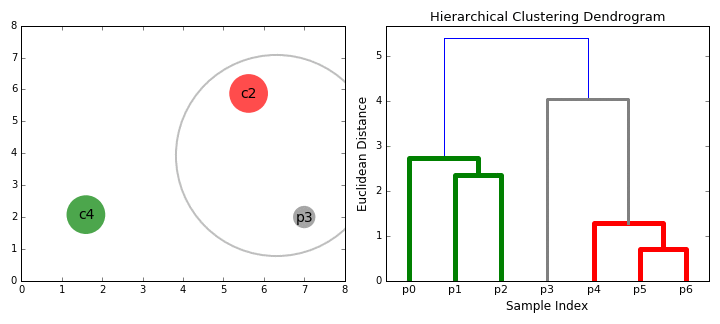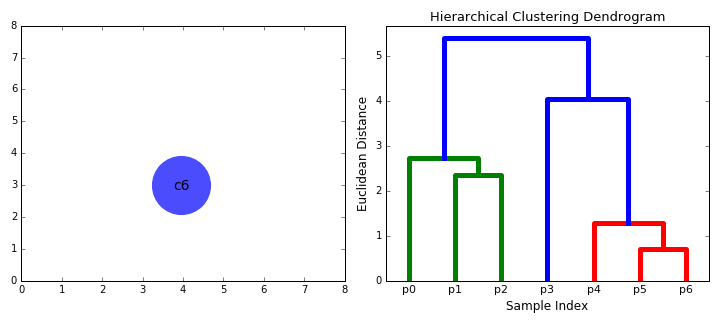
1. cominciamo con il trattamento di dati, un unico cluster.e se ci sono X i punti dati in nostro dataset quindi abbiamo X cluster. Selezioniamo quindi una metrica di distanza che misura la distanza tra due cluster., Ad esempio, useremo il collegamento medio che definisce la distanza tra due cluster come la distanza media tra i punti dati nel primo cluster e i punti dati nel secondo cluster.
2. Su ogni iterazione, combiniamo due cluster in uno. I due cluster da combinare sono selezionati come quelli con il legame medio più piccolo. Cioè secondo la nostra metrica di distanza selezionata, questi due cluster hanno la distanza più piccola tra loro e quindi sono i più simili e dovrebbero essere combinati.
3. Il passaggio 2 viene ripetuto fino a raggiungere la radice dell’albero i.,e abbiamo solo un cluster che contiene tutti i punti dati. In questo modo possiamo selezionare quanti cluster vogliamo alla fine, semplicemente scegliendo quando smettere di combinare i cluster cioè quando smettiamo di costruire l’albero!

Il clustering gerarchico non richiede di specificare il numero di cluster e possiamo persino selezionare quale numero di cluster sembra migliore poiché stiamo costruendo un albero. Inoltre, l’algoritmo non è sensibile alla scelta della metrica della distanza; tutti tendono a funzionare altrettanto bene mentre con altri algoritmi di clustering, la scelta della metrica della distanza è fondamentale., Un caso d’uso particolarmente valido dei metodi di clustering gerarchico è quando i dati sottostanti hanno una struttura gerarchica e si desidera ripristinare la gerarchia; altri algoritmi di clustering non possono farlo. Questi vantaggi del clustering gerarchico hanno il costo di una minore efficienza, in quanto ha una complessità temporale di O(n3), a differenza della complessità lineare di K-Means e GMM.