Icosaedro (Italiano)

L’icosaedro regolare è uno dei cinque solidi platonici. È un poliedro regolare convesso composto da venti facce triangolari, con cinque che si incontrano in ciascuno dei dodici vertici. Ha 30 bordi e 12 vertici. Il suo poliedro doppio è il dodecaedro.,

Dimensione

Se la lunghezza del bordo di un icosaedro regolare è , il raggio della sfera circoscritta (quella che tocca l’icosaedro a tutti i vertici) è

e il raggio della sfera inscritta (tangente per ciascuna delle facce dell’icosaedro) è

mentre la midradius, che tocca al centro di ogni lato, è

dove 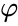(chiamato anche ) è il rapporto aureo.,

Area e volume

superficie e il volume di un icosaedro regolare di lunghezza del bordo sono:

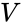
coordinate Cartesiane

I seguenti coordinate Cartesiane definiscono i vertici di un icosaedro con bordo di lunghezza 2, centrata sull’origine:

dove è il rapporto aureo (scritto anche τ)., Si noti che questi vertici formano cinque serie di tre rettangoli dorati reciprocamente centrati e reciprocamente ortogonali.

I 12 bordi di un ottaedro regolare possono essere partizionati nel rapporto aureo in modo che i vertici risultanti definiscano un icosaedro regolare. Questo viene fatto posizionando prima i vettori lungo i bordi dell’ottaedro in modo tale che ogni faccia sia delimitata da un ciclo, quindi suddividendo in modo simile ciascun bordo nella media aurea lungo la direzione del suo vettore., I cinque ottaedri che definiscono un dato icosaedro formano un composto poliedrico regolare, così come i due icosaedri che possono essere definiti in questo modo da un dato ottaedro.

Costruzione con un sistema di linee equiangolari

La seguente costruzione dell’icoshaedron evita calcoli noiosi nel campo numerico necessario in approcci più elementari.

L’esistenza dell’icosaedro equivale all’esistenza di sei linee equiangolari in ., Infatti, intersecando un tale sistema di linee equiangolari con una sfera euclidea centrata alla loro intersezione comune si ottengono i dodici vertici di un icosaedro regolare come si può facilmente verificare. Al contrario, supponendo l’esistenza di un icosaedro regolare, le linee definite dalle sue sei coppie di vertici opposti formano un sistema equiangolare.

Per costruire un tale sistema equiangolare, iniziamo con la matrice

di dimensione quadrata ., (Mnemonico: la matrice codifica gli angoli, acuti per una voce positiva, ottusi altrimenti, tra cinque vertici ciclicamente consecutivi adiacenti ad un primo vertice di un icosaedro centrato all’origine.)

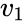
Un calcolo semplice produce . Ciò implica che ha autovalori , entrambi con molteplicità 3 poiché è simmetrico e di traccia 0., La matrice induce thusan struttura Euclidea su lo spazio quoziente che è isomorfi visto che il kernel di ha dimensione 3. L’immagine sotto la proiezione dei sei assi nel moduli così asystem di sei equiangular linee si intersecano pairwise comuni angolo acuto di ., La proiezione ortogonale di sul-eigenspace di produce così i dodici vertici dell’icosaedro.

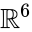
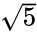
Una seconda costruzione semplice dell’icosaedro utilizza la teoria della rappresentazione del gruppo alternato agendo per isometria diretta sull’icosaedro.

Stellazioni

Secondo le regole specifiche definite nel libro I cinquantanove icosaedri, sono state identificate 59 stellazioni per l’icosaedro regolare. La prima forma è l’icosaedro stesso., Uno è un solido Kepler-Poinsot regolare. Tre sono poliedri composti regolari.

21 di 59 stellations

Le facce dell’icosaedro esteso verso l’esterno, come i piani si intersecano, la definizione di regioni di spazio, come mostrato da questo stellation diagramma delle intersezioni in un unico piano.,

Geometric relations

Icosahedron as a snub tetrahedron.,

Icosahedron as an alternated truncated octahedron.

There are distortions of the icosahedron that, while no longer regular, are nevertheless vertex-uniform., Questi sono invarianti sotto le stesse rotazioni del tetraedro, e sono in qualche modo analoghi al cubo snub e al dodecaedro snub, incluse alcune forme che sono chirali e alcune con simmetria Th, cioè hanno diversi piani di simmetria dal tetraedro. L’icosaedro ha un gran numero di stellazioni, tra cui uno dei poliedri di Kepler-Poinsot e alcuni dei composti regolari, che potrebbero essere discussi qui.

L’icosaedro è unico tra i solidi platonici in possesso di un angolo diedro non inferiore a 120°. Il suo angolo diedro è di circa 138,19°.,ss di 120° e non può essere utilizzato come facce di un convesso regolare poliedro perché una tale costruzione non soddisfano il requisito di almeno tre facce che si incontrano in un vertice e lasciare un positivo difetto per la piegatura in tre dimensioni, icosahedra non possono essere utilizzati come celle di un convesso regolare policoro, perché, allo stesso modo, almeno tre celle devono rispondere a bordo e lasciare un positivo difetto per la piegatura in quattro dimensioni (in generale per un convesso polytope nel dimensioni, almeno tre aspetti devono rispondere a un picco e lasciare un positivo difetto per la piegatura in n-space)., Tuttavia, quando combinato con celle adatte con angoli diedri più piccoli, gli icosaedri possono essere usati come celle in polichora semi-regolare (ad esempio la cella snub 24), proprio come gli esagoni possono essere usati come facce in poliedri semi-regolari (ad esempio l’icosaedro troncato). Infine, i politopi non convessi non hanno gli stessi requisiti rigorosi dei politopi convessi, e gli icosaedri sono infatti le cellule dell’icosaedro a 120 celle, uno dei dieci polichori regolari non convessi.

Un icosaedro può anche essere chiamato bipiramide pentagonale gyroelongated., Può essere scomposto in una piramide pentagonale gyroelongated e una piramide pentagonale o in un antiprisma pentagonale e due piramidi pentagonali uguali.

L’icosaedro può anche essere chiamato un tetraedro snub, poiché la snubificazione di un tetraedro regolare dà un icosaedro regolare., In alternativa, utilizzando la nomenclatura per poliedri snub che si riferisce a un cubo snub come un cuboctaedro snub (cuboctaedro = cubo rettificato) e un dodecaedro snub come icosidodecaedro snub (icosidodecaedro = dodecaedro rettificato), si può chiamare l’icosaedro l’ottaedro snub (ottaedro = tetraedro rettificato).

Un icosaedro rettificato forma un icosidodecaedro.

Icosaedro vs dodecaedro

Quando un icosaedro è inscritto in una sfera, occupa meno del volume della sfera (60,54%) di un dodecaedro inscritto nella stessa sfera (66,49%).,

Inoltre, poiché questi sono duali, è possibile trasformare l’uno nell’altro(Vedi sotto).,

Icosahedron

Truncated icosahedron

Icosidodecahedron

Truncated dodecahedron

Dodecahedron

Uses and natural forms

In 1904, Ernst Haeckel described a number of species of Radiolaria, including Circogonia icosahedra, whose skeleton is shaped like a regular icosahedron. A copy of Haeckel’s illustration for this radiolarian appears in the article on regular polyhedra.

	In alcuni giochi di ruolo, il dado a venti lati (in breve, d20) viene utilizzato per determinare il successo o il fallimento di un’azione. Questo dado ha la forma di un icosaedro regolare. Può essere numerato da” 0 “a” 9 “due volte (nella quale forma di solito serve come un dado a dieci lati, o d10), ma la maggior parte delle versioni moderne sono etichettate da” 1 “a”20”. Vedere Sistema d20.,

Un icosaedro è il gioco tridimensionale per Icosagame, precedentemente noto come Ico Crystal Game.

Un icosaedro viene utilizzato nel gioco da tavolo Scattergories per scegliere una lettera dell’alfabeto. Sei lettere poco usate, come X, Q e Z, vengono omesse.

All’interno di una palla magica 8, varie risposte alle domande sì-no sono stampate su un icosaedro regolare.

L’icosaedro visualizzato in forma funzionale è visibile nella tonalità chiara Sol de la Flor., Il rosone formato dai pezzi sovrapposti mostra una somiglianza con il fiore di Frangipani.

Se ogni bordo di un icosaedro viene sostituito da un resistore di un ohm, la resistenza tra i vertici opposti è di 0,5 ohm e quella tra i vertici adiacenti di 11/30 ohm.

Il gruppo di simmetria dell’icosaedro è isomorfo al gruppo alternato su cinque lettere. Questo gruppo semplice non abeliano è l’unico sottogruppo normale non banale del gruppo simmetrico su cinque lettere., Poiché il gruppo di Galois dell’equazione quintica generale è isomorfo al gruppo simmetrico su cinque lettere, e il fatto che il gruppo icosaedrico sia semplice e non abeliano significa che le equazioni quintiche non devono avere una soluzione nei radicali. La dimostrazione del teorema di Abel-Ruffini utilizza questo semplice fatto, e Felix Klein ha scritto un libro che ha fatto uso della teoria delle simmetrie icosaedriche per derivare una soluzione analitica per l’equazione quintica generale.,

Vedi anche

Modello:Wiktionarypar

• icosaedro Troncato
• Regolare poliedro
• Geodetica griglie di utilizzare un modo iterativo che si incrociavano icosaedro per generare griglie su una sfera
• Jessen dell’icosaedro

Modello:Wikisource1911Enc

Modello:Commonscat

• Weisstein, Eric W., “Icosaedro” da MathWorld.
• Modelli cartacei dell’icosaedro
• I poliedri uniformi
• K. J. M., MacLean, Un’analisi geometrica dei cinque solidi platonici e altri poliedri semi-regolari
• Modello icosaedro interattivo-funziona direttamente nel tuo browser web
• Realtà virtuale Poliedri L’Enciclopedia dei poliedri
• Tulane.,edu è Una discussione di super struttura e l’icosaedro
• Carta Modelli di Poliedri Molti link
• Origami Poliedri – Modelli è realizzato con un Origami Modulare
• il video di icosaedrica specchio è una scultura

Modello:Poliedri

az:Ikosaedrca:Icosàedrecs:Dvacetistěnda:Ikosaederet:Ikosaeedereo:Dudekedrofa:بیستوجهیit:Icosaedrohe:איקוסהדרוןlv:Ikosaedrshu:Ikozaédernl:Icosaëderno:Ikosaederpl:Dwudziestościan foremnypt:Icosaedrosimple:Icosahedronsq:Ikosaedri ho rregulltsr:Икосаедарsv:Ikosaederta:è scoppiata முக்கோணகம்th:ทรงยี่สิบหน้าuk:Ікосаедр.