Introduzione alla filosofia: Logica

C’è una visione antica, ancora ampiamente diffusa, che ciò che rende gli esseri umani speciali—ciò che ci distingue dalle “bestie del campo”—è che siamo razionali. In cosa consiste la razionalità? Questa è una domanda irritata, ma una possibile risposta va più o meno così: manifestiamo la nostra razionalità impegnandoci in attività che coinvolgono il ragionamento—facendo affermazioni e sostenendole con ragioni, agendo in accordo con ragioni e credenze, attingendo inferenze da prove disponibili, e così via.,

Questa attività di ragionamento può essere fatta bene e può essere fatta male; può essere fatta correttamente o in modo errato. La logica è la disciplina che mira a distinguere il buon ragionamento dal male.

Un buon ragionamento non è necessariamente un ragionamento efficace. Infatti, come vedremo in un capitolo successivo sugli errori logici, il cattivo ragionamento è pervasivo e spesso estremamente efficace—nel senso che le persone sono spesso persuase da esso. Nella logica, lo standard della bontà non è l’efficacia nel senso di persuasività, ma piuttosto la correttezza secondo le regole logiche.,

Ad esempio, considera Hitler. Persuase un’intera nazione ad accettare una serie di proposte non solo false, ma addirittura malvagie. Non sarete sorpresi di sentire che se si esamina criticamente, il suo ragionamento non passa adunata logica. Gli argomenti di Hitler erano efficaci, ma non logicamente corretti. Inoltre, le sue tecniche persuasive vanno oltre il ragionamento nel senso di sostenere affermazioni con ragioni. Hitler si basava su minacce, manipolazioni emotive, affermazioni non supportate, ecc. Ci sono molti trucchi retorici che si possono usare per persuadere.,

In logica, studiamo le regole e le tecniche che ci permettono di distinguere il ragionamento buono e corretto dal ragionamento cattivo e scorretto.

Poiché esistono una varietà di diversi tipi di ragionamento e metodi con cui valutare ciascuno di questi tipi, oltre a varie opinioni divergenti su ciò che costituisce un ragionamento corretto, ci sono molti approcci all’impresa logica. Si parla di logica, ma anche di logica. Una logica è solo un insieme di regole e tecniche per distinguere il buon ragionamento dal cattivo., Una logica deve formulare standard precisi per valutare il ragionamento e sviluppare metodi per applicare tali standard a particolari istanze.

Nozioni di base

Il ragionamento implica affermazioni o dichiarazioni—rendendole e sostenendole con ragioni, disegnandone le conseguenze. Le proposizioni sono le cose che rivendichiamo, affermiamo, affermiamo.

Le proposizioni sono il tipo di cose che possono essere vere o false. Sono espressi da frasi dichiarative., Usiamo tali frasi per fare ogni sorta di asserzioni, dalle questioni di routine di fatto (“la Terra ruota intorno al Sole”), alle grandi tesi metafisiche (“la realtà è un assoluto immutabile, senza caratteristiche, unificato”), alle affermazioni sulla moralità (“è sbagliato mangiare carne”).

È importante distinguere le frasi nell’umore dichiarativo, che esprimono proposizioni, dalle frasi in altri stati d’animo, che non lo fanno. Frasi interrogative, ad esempio, fanno domande (“Sta piovendo?”), e le frasi imperative emettono comandi (“Non bere cherosene.”)., Non ha senso chiedersi se questo tipo di frasi esprimono verità o falsità, quindi non esprimono proposizioni.

Distinguiamo anche le proposizioni dalle frasi che le esprimono, perché una singola proposizione può essere espressa da frasi diverse. “It’s raining” e “es regnet” esprimono entrambi la proposizione che sta piovendo; una frase lo fa in inglese, l’altra in tedesco. Anche, “Giovanni ama Maria” e “Maria è amata da Giovanni” entrambi esprimono la stessa proposizione.

L’unità fondamentale del ragionamento è l’argomento., Nella logica, per “argomento”non intendiamo un disaccordo, una partita urlante; piuttosto, definiamo precisamente il termine:

Argomento = un insieme di proposizioni, una delle quali, la conclusione, è (dovrebbe essere) supportata dalle altre, le premesse.

Se stiamo ragionando facendo affermazioni e sostenendole con ragioni, allora l’affermazione di cui viene eseguito il backup è la conclusione di un argomento; le ragioni fornite per sostenerlo sono le premesse dell’argomento., Se stiamo ragionando disegnando un’inferenza da un insieme di affermazioni, allora l’inferenza che tracciamo è la conclusione di un argomento, e le affermazioni da cui è tratto sono le premesse.

Includiamo la siepe tra parentesi—”dovrebbe essere”—nella definizione per fare spazio a argomenti errati. Un cattivo argomento, molto grosso modo, è quello in cui le premesse non supportano la conclusione; le premesse di un buon argomento in realtà supportano la conclusione.

Analisi degli argomenti

Il seguente passaggio esprime un argomento:

Così fa questo passaggio:

Ancora una volta, lo scopo ultimo della logica è valutare gli argomenti—distinguere il bene dal male. Per fare ciò richiede distinzioni, definizioni, principi e tecniche che saranno delineate nei capitoli successivi. Per ora, ci concentreremo sull’identificazione e la ricostruzione degli argomenti.

Il primo compito è quello di spiegare gli argomenti—di indicare esplicitamente le loro premesse e conclusioni., Un modo perspicuo per farlo è semplicemente elencare frasi dichiarative che esprimono le proposizioni pertinenti, con una linea che separa le premesse dalla conclusione, quindi:

1. McDonald’s paga i loro lavoratori salari molto bassi.
2. Gli animali che forniscono carne di McDonald sono allevati in condizioni deplorevoli.
3. Il cibo di McDonald è molto malsano.
4. /\quindi non dovresti mangiare da McDonald’s.

Questa è una spiegazione del primo passaggio argomentativo sopra., Per identificare la conclusione di un argomento, è utile chiedersi: “Che cosa sta cercando di convincermi a credere dicendo queste cose? Qual è il punto finale di questo passaggio?” La risposta è abbastanza chiara in questo caso. Un altro indizio su cosa sta succedendo nel passaggio è fornito dalla parola “perché” nella terza frase. Insieme ad altre parole, come “poiché” e “per”, indica la presenza di una premessa. Possiamo chiamare tali parole premessa marcatori. Il simbolo “/∴” può essere letto come abbreviazione di “therefore.,”Insieme a espressioni come “di conseguenza”,” così”, “ne consegue che” e” che implica che”,” quindi ” è un indicatore che la conclusione dell’argomento sta per seguire. Chiamiamo tali locuzioni marcatori di conclusione. Tale marcatore non è presente nel primo argomento, ma ne vediamo uno nel secondo, che può essere spiegato così:

1. L’universo è vasto e complesso.
2. L’universo mostra un sorprendente grado di ordine.
3. I pianeti orbitano attorno al sole secondo le leggi regolari.
4. Le parti più piccole degli animali sono disposte precisamente per servire i loro scopi.,
5. Tale ordine e complessità non possono sorgere a caso.
6. / \quindi l’universo deve essere il prodotto di un progettista di enorme potere e intelletto: Dio.

Diversi punti di confronto alla nostra prima spiegazione sono degni di nota qui. In primo luogo, come detto, siamo stati avvisati della conclusione dalla parola “pertanto.”In secondo luogo, questo passaggio richiedeva molto più parafrasi del primo. La seconda frase è interrogativa, non dichiarativa, e quindi non esprime una proposizione., Poiché gli argomenti sono, per definizione, raccolte di proposizioni, dobbiamo limitarci a frasi dichiarative quando le spieghiamo. Poiché la risposta alla domanda retorica della seconda frase è chiaramente “sì”, parafrasiamo come mostrato. La terza frase esprime due proposizioni, quindi nella nostra spiegazione le separiamo; ognuna è una premessa.

Quindi a volte, quando spieghiamo un argomento, dobbiamo prendere ciò che è presente nel passaggio argomentativo e cambiarlo leggermente, in modo che tutte le frasi che scriviamo esprimano le proposizioni presenti nell’argomento., Questo è parafrasando. Altre volte, dobbiamo fare ancora di più. Ad esempio, potremmo dover introdurre proposizioni che non sono esplicitamente menzionate all’interno del passaggio argomentativo, ma sono indubbiamente utilizzate all’interno del ragionamento dell’argomento.

C’è una parola greca per passaggi argomentativi che lasciano certe proposizioni non dichiarate: entimemi. Ecco un esempio:

C’è una premessa implicita in agguato in background qui—qualcosa che non è stato detto, ma che deve essere vero per l’argomento di passare attraverso. Abbiamo bisogno di un’affermazione che colleghi la premessa alla conclusione—che colmi il divario tra loro. Qualcosa di simile: un Dio che ama tutto non permetterebbe alle persone innocenti di soffrire. O forse: la sofferenza diffusa è incompatibile con l’idea di una divinità che ama tutto. La premessa indica la sofferenza, mentre la conclusione riguarda Dio; queste proposizioni collegano queste due affermazioni., Una spiegazione completa del passaggio argomentativo renderebbe esplicita una proposizione come questa:

1. Molte persone innocenti in tutto il mondo stanno soffrendo.
2. Un Dio che ama tutto non permetterebbe alle persone innocenti di soffrire.
3. / \quindi non ci può essere un Dio che ama tutto.

Questo è il marchio dei tipi di premesse tacite che vogliamo scoprire: se sono false, minano l’argomento., Spesso, premesse come questa non sono dichiarate per un motivo: sono affermazioni controverse da sole, che richiedono prove per sostenerle; quindi l’argomentatore le lascia fuori, preferendo non impantanarsi. Quando li tiriamo fuori, tuttavia, possiamo forzare uno scambio dialettico più robusto, concentrando l’argomento sul cuore della questione. In questo caso, una discussione sulla compatibilità della bontà di Dio e del male nel mondo sarebbe in ordine. C’è molto da dire su questo argomento., Filosofi e teologi hanno sviluppato argomenti elaborati nel corso dei secoli per difendere l’idea che la bontà di Dio e la sofferenza umana siano in realtà compatibili.

Finora, la nostra analisi degli argomenti non è stata particolarmente approfondita. Abbiamo notato l’importanza di identificare le conclusioni e di indicare chiaramente le premesse, ma non abbiamo esaminato i modi in cui gruppi di premesse possono sostenere le loro conclusioni. Abbiamo semplicemente osservato che, collettivamente, le premesse forniscono sostegno alle conclusioni., Non abbiamo esaminato come lo fanno, quali tipi di relazioni hanno l’uno con l’altro. Ciò richiede un’analisi più approfondita.

Spesso, diverse premesse supporteranno una conclusione—o un’altra premessa—individualmente, senza l’aiuto di altri. Considera questo semplice argomento:

Le proposizioni 1 e 2 supportano la conclusione, proposizione 3—e lo fanno indipendentemente. Ognuno ci dà una ragione per credere che la guerra era ingiusta, e ciascuno si erge come una ragione anche se dovessimo supporre che l’altro non fosse vero; questo è il marchio di premesse indipendenti.

Può essere utile, specialmente quando gli argomenti sono più complessi, disegnare diagrammi che descrivono le relazioni tra premesse e conclusioni., Potremmo descrivere l’argomento sopra come segue:

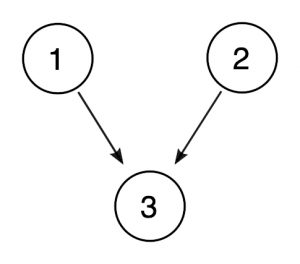
In tale diagramma, i numeri cerchiati rappresentano le proposizioni e le frecce rappresentano la relazione di supporto da una proposizione all’altra. Poiché le proposizioni 1 e 2 supportano ciascuna 3 in modo indipendente, ottengono le proprie frecce.

Sono possibili altre relazioni tra i locali. A volte, le premesse forniscono supporto per le conclusioni solo indirettamente, dandoci una ragione per credere a qualche altra premessa, che è intermedia tra le due affermazioni., Considera il seguente argomento:

In questo esempio, la proposizione 1 fornisce il supporto per la proposizione 2 (la parola “quindi” è un indizio), mentre la proposizione 2 supporta direttamente la conclusione in 3., Descriveremmo le relazioni tra queste proposizioni così:

A volte le premesse devono lavorare insieme per fornire supporto per un’altra affermazione, non perché una di esse fornisca motivo per credere all’altra, ma perché nessuna delle due fornisce il supporto necessario da sola; chiamiamo tali proposizioni premesse congiunte. Considera quanto segue:

In questo argomento, né la premessa 1 né la premessa 2 supportano la conclusione da sola; piuttosto, la seconda premessa, per così dire, fornisce una chiave che sblocca la conclusione dalla premessa condizionale 1. Possiamo indicare tale interdipendenza schematicamente con parentesi, quindi:

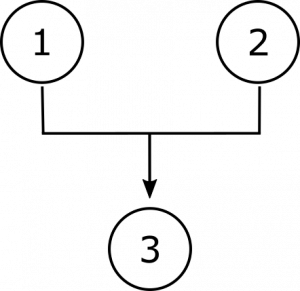
Diagrammare argomenti in questo modo può essere utile sia per capire come funzionano sia per informare qualsiasi tentativo di impegnarsi criticamente con loro., Nella prima argomentazione si vede chiaramente che qualsiasi considerazione contraria a una delle premesse indipendenti non comprometterà completamente il sostegno alla conclusione, poiché esiste ancora un’altra premessa che le fornisce un certo grado di sostegno. Nel secondo argomento, però, le ragioni che dicono contro la seconda premessa taglierebbero il supporto per la conclusione alla radice; e qualsiasi cosa contraria alla prima premessa lascerà il secondo bisognoso di supporto. E nel terzo argomento, considerazioni contrarie a una delle premesse comuni mineranno il sostegno alla conclusione., Soprattutto quando gli argomenti sono più complessi, tali ausili visivi possono aiutarci a riconoscere tutte le inferenze contenute all’interno dell’argomento.

Forse sarà utile concludere considerando un argomento leggermente più complesso. Consideriamo la natura dei numeri:

La conclusione di questo argomento è l’ultima proposizione, che i numeri sono oggetti astratti. Si noti che la prima premessa ci dà una scelta tra questa affermazione e un’alternativa—che sono concreti. La seconda premessa nega quell’alternativa, e così le premesse 1 e 2 stanno lavorando insieme per sostenere la conclusione:

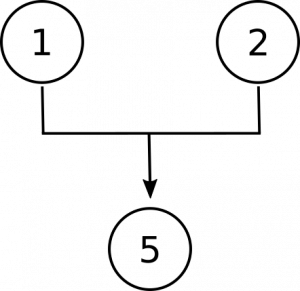
Ora dobbiamo fare spazio nel nostro diagramma per le proposizioni 3 e 4. Sono lì per darci ragioni per credere che i numeri non siano oggetti concreti., In primo luogo, affermando che i numeri non si trovano nello spazio come lo sono gli oggetti concreti, e in secondo luogo affermando che i numeri non interagiscono con altri oggetti, come fanno gli oggetti concreti. Queste sono ragioni separate e indipendenti per credere che non siano concrete, quindi finiamo con questo diagramma:

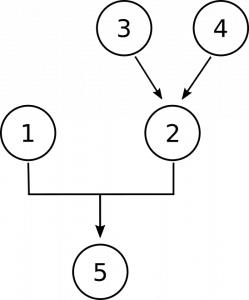
Logica e filosofia

Al centro dell’impresa logica c’è una domanda filosofica: cosa rende un buon argomento? Cioè, che cosa è per una serie di affermazioni fornire supporto per qualche altra affermazione? O forse: quando siamo giustificati nel disegnare inferenze?, Per rispondere a queste domande, i logici hanno sviluppato un’ampia varietà di sistemi logici, coprendo diversi tipi di argomenti e applicando diversi principi e tecniche. Molti degli strumenti sviluppati nella logica possono essere applicati oltre i confini della filosofia. Il matematico che dimostra un teorema, l’informatico che programma un computer, il linguista che modella la struttura del linguaggio—tutti questi stanno usando metodi logici., Poiché la logica ha un’applicazione così ampia e, a causa della sofisticazione formale/matematica di molti sistemi logici, occupa un posto unico nel curriculum filosofico. Una classe di logica è in genere a differenza di altre classi di filosofia in quanto pochissimo tempo viene speso direttamente impegnandosi e tentando di rispondere alle “grandi domande”; piuttosto, si arriva molto rapidamente al business dell’apprendimento dei formalismi logici. Le domande che la logica sta cercando di rispondere sono importanti domande filosofiche, ma le tecniche sviluppate per rispondere a loro sono degne di studio da sole.,

Questo non significa, tuttavia, che dovremmo pensare alla logica e alla filosofia come semplicemente tangenzialmente correlate; al contrario, sono profondamente intrecciate. Per tutte le campane formali e fischietti presenti nel più recente sistema logico di fascia alta, in fondo è parte di uno sforzo per rispondere alla domanda fondamentale di ciò che segue da cosa. Inoltre, la logica è utile al filosofo praticante in almeno altri tre modi.

I filosofi cercano di rispondere a domande profonde e vessatorie—sulla natura della realtà, su cosa costituisce una buona vita, su come creare una società giusta e così via., Danno le loro risposte a queste domande e le sostengono con ragioni. Poi altri filosofi considerano i loro argomenti e rispondono con elaborazioni e critiche—argomenti propri. La filosofia è condotta e fa progressi attraverso lo scambio di argomenti. Dal momento che sono lo strumento principale del loro mestiere, filosofi meglio sapere un po ‘ di qualcosa su ciò che rende per buoni argomenti! La logica, quindi, è essenziale per la pratica della filosofia.,

Ma la logica non è solo uno strumento per valutare argomenti filosofici; ha alterato il corso della conversazione filosofica in corso. Mentre i logici sviluppavano sistemi formali per modellare la struttura di una gamma sempre più ampia di pratiche discorsive, i filosofi sono stati in grado di applicare le loro intuizioni direttamente ai problemi filosofici tradizionali e riconoscere vie di indagine precedentemente nascoste. Dal volgere del 20 ° secolo in particolare, la proliferazione di nuovi approcci nella logica ha scatenato una rivoluzione nella pratica della filosofia., Non è troppo esagerato dire che gran parte della storia della filosofia nel 20 ° secolo costituiva un tentativo continuo di affrontare i nuovi sviluppi della logica e l’attenzione filosofica sul linguaggio che sembravano richiedere. Nessun argomento filosofico—dalla metafisica all’etica all’epistemologia e oltre-è stato toccato da questa rivoluzione.

Infine, la logica stessa è la fonte di affascinanti domande filosofiche. La domanda fondamentale al suo cuore-che cosa è per una pretesa di seguire da altri?,- ramifica in una miriade di direzioni, fornendo terreno fertile per la speculazione filosofica. C’è la logica, e poi c’è la filosofia della logica. Si dice che la logica sia “formale”, ad esempio. Che significa? È una domanda sorprendentemente difficile a cui rispondere. Le nostre formulazioni logiche più semplici di frasi condizionali (quelle che coinvolgono “se”), portano a paradossi apparenti. Come dovrebbero essere risolti? I nostri formalismi dovrebbero essere modificati per catturare meglio i significati del linguaggio naturale dei condizionali? Qual è la corretta relazione tra sistemi logici e linguaggi naturali, comunque?,

Tradizionalmente, la maggior parte dei logici ha accettato che la logica dovrebbe essere “bivalente”: ogni proposizione è vera o falsa. Ma le lingue naturali contengono termini vaghi i cui confini di applicabilità non sono sempre chiari. Ad esempio,” calvo”: per alcuni soggetti, potremmo essere inclini a dire che sono sulla buona strada per la calvizie completa, ma non ancora del tutto; d’altra parte, saremmo riluttanti a dire che non sono calvi. Ci sono casi intermedi. Per questi casi, potremmo voler dire, ad esempio, che la proposizione che Fredo è calvo non è né vera né falsa., Alcuni logici hanno sviluppato logiche che non sono bivalenti, per affrontare questo tipo di fenomeno linguistico. Alcuni aggiungono un terzo valore di verità: “né” o “indeterminato”, per esempio. Altri introducono infiniti gradi di verità (questo è chiamato “logica fuzzy”). Queste logiche si discostano dagli approcci tradizionali. Sono quindi sbagliati in un certo senso? O hanno ragione e i tradizionalisti sbagliano? O stiamo anche facendo una domanda sensata quando chiediamo se un particolare sistema logico è giusto o sbagliato?, Possiamo essere i cosiddetti “pluralisti” logici, accettando una varietà di logiche incompatibili, a seconda, ad esempio, se sono utili?

Questo tipo di domande vanno oltre lo scopo di questo testo introduttivo, ovviamente. Sono inclusi per darvi un senso di quanto lontano si può prendere lo studio della logica. Il compito per ora, però, è quello di iniziare quello studio.