
Leonardo pisano (Fibonacci) (c.1170-1250)
13 ° Secolo italiano Leonardo di Pisa, meglio conosciuto con il soprannome di Fibonacci, è stato forse il più talentuoso Occidentale matematico del Medioevo. Poco si sa della sua vita, tranne che egli era il figlio di un funzionario doganale e, come un bambino, ha viaggiato in tutto il Nord Africa con il padre, dove ha imparato a conoscere la matematica araba., Al suo ritorno in Italia, ha contribuito a diffondere questa conoscenza in tutta Europa, mettendo così in moto un ringiovanimento della matematica europea, che era rimasto in gran parte dormiente per secoli durante il Medioevo.
In particolare, nel 1202, scrisse un libro estremamente influente chiamato “Liber Abaci” (“Libro di calcolo”), in cui promosse l’uso del sistema numerico indù-arabo, descrivendone i numerosi benefici per i mercanti e i matematici rispetto al goffo sistema di numeri romani allora in uso in Europa., Nonostante i suoi evidenti vantaggi, assorbimento del sistema in Europa lenta (questo era, dopo tutto, durante il tempo delle Crociate contro l’Islam, un tempo in cui nulla di arabo era visto con grande sospetto), e numeri arabi sono stati addirittura vietato nella città di Firenze, nel 1299, con il pretesto che erano più facili da falsificare rispetto a numeri Romani. Tuttavia, il buon senso alla fine ha prevalso e il nuovo sistema è stato adottato in tutta Europa entro il 15 ° secolo, rendendo il sistema romano obsoleto., La notazione della barra orizzontale per le frazioni è stata anche utilizzata per la prima volta in questo lavoro (anche se seguendo la pratica araba di posizionare la frazione a sinistra del numero intero).
Sequenza di Fibonacci

La scoperta della famosa sequenza di Fibonacci
di Fibonacci è noto, anche se, per la sua introduzione in Europa di una particolare sequenza di numeri, che è diventato noto come Fibonacci o la Sequenza di Fibonacci., Ha scoperto la sequenza-la prima sequenza numerica ricorsiva conosciuta in Europa – considerando un problema pratico nel “Liber Abaci” che coinvolge la crescita di un’ipotetica popolazione di conigli basata su ipotesi idealizzate. Notò che, dopo ogni generazione mensile, il numero di coppie di conigli aumentava da 1 a 2 a 3 a 5 a 8 a 13, ecc., e identificò come la sequenza progrediva aggiungendo i due termini precedenti (in termini matematici, Fn = Fn-1 + Fn-2), una sequenza che in teoria potrebbe estendersi indefinitamente.,
La sequenza, che era stata effettivamente conosciuta dai matematici indiani fin dal vi secolo, ha molte proprietà matematiche interessanti, e molte delle implicazioni e delle relazioni della sequenza non furono scoperte fino a diversi secoli dopo la morte di Fibonacci., Ad esempio, la sequenza si rigenera in alcuni modi sorprendenti: ogni terzo numero F è divisibile per 2 (F3 = 2), ogni quarto numero F è divisibile per 3 (F4 = 3), ogni quinto numero F è divisibile per 5 (F5 = 5), ogni sesto numero F è divisibile per 8 (F6 = 8), ogni settimo numero F è divisibile per 13 (F7 = 13), ecc., I numeri della sequenza è stato anche trovato per essere onnipresente in natura: tra le altre cose, molte specie di piante da fiore hanno un numero di petali nella sequenza di Fibonacci; le disposizioni a spirale di ananas si verificano in 5s e 8s, quelli di pigne in 8s e 13s, e i semi di teste di girasole in 21s, 34s, 55s o anche termini superiori nella sequenza; ecc.,
Il Rapporto aureo φ
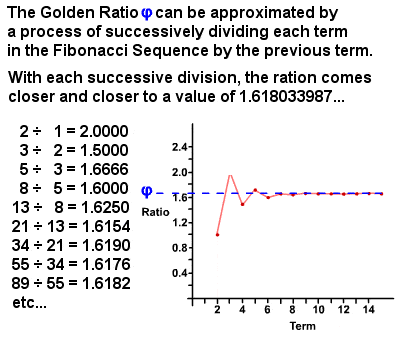
Il Rapporto aureo φ può essere derivato dalla Sequenza di Fibonacci
Nel 1750, Robert Simson notato che il rapporto di ogni termine della Sequenza di Fibonacci per il precedente termine approcci, con una precisione sempre maggiore, la maggiore, i termini, un rapporto di circa 1 : 1.6180339887 (in realtà è un numero irrazionale è uguale a (1 + √5)⁄2 che è stato calcolato con migliaia di cifre decimali)., Questo valore è indicato come il Rapporto aureo, noto anche come la Media aurea, Sezione aurea, Proporzione divina, ecc, ed è di solito indicato con la lettera greca phi φ (o talvolta la lettera maiuscola Phi Φ). Essenzialmente, due quantità sono nel Rapporto aureo se il rapporto tra la somma delle quantità e la quantità più grande è uguale al rapporto tra la quantità più grande e quella più piccola. Il Rapporto aureo stesso ha molte proprietà uniche, come 1 φ φ = φ – 1 (0,618…) e φ2 = φ + 1 (2,618 φ), e ci sono innumerevoli esempi di esso che si trovano sia in natura che nel mondo umano.,
Un rettangolo con i lati in rapporto di 1 : φ è conosciuto come un Rettangolo aureo, e molti artisti e architetti di tutta la storia (che risale all’antico Egitto e della Grecia, ma particolarmente popolare nel Rinascimento l’arte di Leonardo da Vinci e dei suoi contemporanei) sono proporzionati le loro opere circa, utilizzando la sezione aurea e Rettangoli d’Oro, che sono ampiamente considerati intrinsecamente piacevole esteticamente. Un arco che collega punti opposti di rettangoli dorati annidati sempre più piccoli forma una spirale logaritmica, nota come Spirale dorata., Il Rapporto aureo e la Spirale dorata possono anche essere trovati in un numero sorprendente di casi in Natura, dalle conchiglie ai fiori alle corna degli animali ai corpi umani ai sistemi di tempesta per completare le galassie.,
Va ricordato, tuttavia, che la Sequenza di Fibonacci era in realtà solo un elemento molto minore nel “Liber Abaci” – infatti, la sequenza ricevette il nome di Fibonacci solo nel 1877 quando Eduouard Lucas decise di rendergli omaggio intitolando la serie dopo di lui – e che Fibonacci stesso non era responsabile dell’identificazione di nessuna delle interessanti proprietà matematiche della sequenza, della sua relazione con la Media aurea e i rettangoli e le Spirali auree, ecc.,
Reticolo di Moltiplicazione
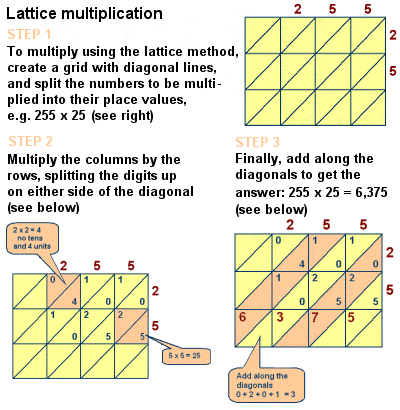
Fibonacci introdotto reticolo di moltiplicazione per l’Europa
Tuttavia, l’influenza del libro di storia medievale matematica è innegabile, e lo fa anche includere discussioni di un certo numero di altri problemi matematici come il Cinese Resto, Teorema perfetto numeri e i numeri primi, formule di calcolo aritmetico serie e per piazza piramidale numeri, Euclidea prove geometriche, e uno studio di equazioni lineari lungo le linee di Diophantus e Al-Karaji., Ha anche descritto il reticolo (o setaccio) metodo di moltiplicazione di moltiplicare grandi numeri, un metodo – originariamente sperimentato da matematici islamici come Al-Khwarizmi – algoritmicamente equivalente alla moltiplicazione lunga.
Nessuno dei due era “Liber Abaci” L’unico libro di Fibonacci, anche se era il suo più importante., Il “Liber Quadratorum” (“Il Libro delle Piazze”), per esempio, è un libro di algebra, pubblicato nel 1225, in cui appare una dichiarazione di quello che ora è chiamato Fibonacci identità di – a volte noto anche come Brahmagupta identità dopo il molto prima matematico Indiano che anche giunse alle stesse conclusioni – che il prodotto di due somme di due quadrati è di per sé una somma di due quadrati ad es. (12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,
| << Back to Medieval Mathematics | Forward to 16th Century Mathematics >> |