Risultati di Apprendimento
- acquisire familiarità con la storia della posizionali sistemi di numero
- Identificare le basi che sono state utilizzate nei sistemi numerici storicamente
- la Conversione di numeri tra le basi
- Utilizzare due diversi metodi per la conversione di numeri tra le basi
Sfondo
Come si può immaginare, lo sviluppo di un sistema di base è un passo importante nel rendere il processo di conteggio più efficiente., Il nostro sistema base-ten probabilmente è nato dal fatto che abbiamo 10 dita (inclusi i pollici) su due mani. Questo è uno sviluppo naturale. Tuttavia, altre civiltà hanno avuto una varietà di basi diverse da dieci. Ad esempio, i nativi del Queensland usavano un sistema base-due, contando come segue: “uno, due, due e uno, due due, molto.”Alcune moderne tribù sudamericane hanno un sistema di base-cinque che conta in questo modo:” uno, due, tre, quattro, mano, mano e uno, mano e due” e così via. I babilonesi usavano un sistema base-sessanta (sessigesimale)., In questo capitolo, concludiamo con un esempio specifico di una civiltà che in realtà ha utilizzato un sistema di base diverso da 10.
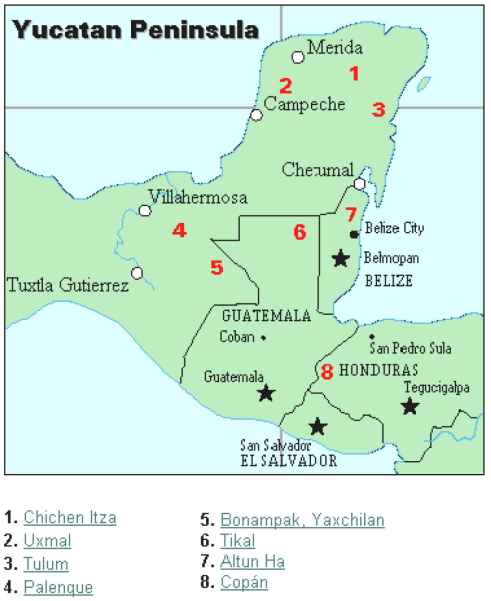 La civiltà Maya è generalmente datata dal 1500 AC al 1700 CE. La penisola dello Yucatan (vedi figura 16) in Messico è stata la scena per lo sviluppo di una delle civiltà più avanzate del mondo antico. I Maya avevano un sofisticato sistema rituale che era supervisionato da una classe sacerdotale. Questa classe di sacerdoti ha sviluppato una filosofia con il tempo come divina ed eterna., Il calendario e i calcoli ad esso correlati erano quindi molto importanti per la vita rituale della classe sacerdotale, e quindi del popolo Maya. In effetti, gran parte di ciò che sappiamo su questa cultura proviene dai loro record di calendario e dai dati astronomici. Un’altra importante fonte di informazioni sui Maya sono gli scritti di padre Diego de Landa, che si recò in Messico come missionario nel 1549.
La civiltà Maya è generalmente datata dal 1500 AC al 1700 CE. La penisola dello Yucatan (vedi figura 16) in Messico è stata la scena per lo sviluppo di una delle civiltà più avanzate del mondo antico. I Maya avevano un sofisticato sistema rituale che era supervisionato da una classe sacerdotale. Questa classe di sacerdoti ha sviluppato una filosofia con il tempo come divina ed eterna., Il calendario e i calcoli ad esso correlati erano quindi molto importanti per la vita rituale della classe sacerdotale, e quindi del popolo Maya. In effetti, gran parte di ciò che sappiamo su questa cultura proviene dai loro record di calendario e dai dati astronomici. Un’altra importante fonte di informazioni sui Maya sono gli scritti di padre Diego de Landa, che si recò in Messico come missionario nel 1549.
 C’erano due sistemi numerali sviluppati dai Maya: uno per la gente comune e uno per i sacerdoti., Non solo questi due sistemi utilizzano simboli diversi, hanno anche utilizzato diversi sistemi di base. Per i sacerdoti, il sistema numerico era governato dal rituale. Si pensava che i giorni dell’anno fossero dei, quindi i simboli formali per i giorni erano teste decorate, come il campione a sinistra Poiché il calendario di base era basato su 360 giorni, il sistema numerico sacerdotale usava un sistema di base misto impiegando multipli di 20 e 360. Questo rende per un sistema di confusione, i dettagli di cui salteremo.,/td>
C’erano due sistemi numerali sviluppati dai Maya: uno per la gente comune e uno per i sacerdoti., Non solo questi due sistemi utilizzano simboli diversi, hanno anche utilizzato diversi sistemi di base. Per i sacerdoti, il sistema numerico era governato dal rituale. Si pensava che i giorni dell’anno fossero dei, quindi i simboli formali per i giorni erano teste decorate, come il campione a sinistra Poiché il calendario di base era basato su 360 giorni, il sistema numerico sacerdotale usava un sistema di base misto impiegando multipli di 20 e 360. Questo rende per un sistema di confusione, i dettagli di cui salteremo.,/td>
The Mayan Number System
Instead, we will focus on the numeration system of the “common” people, which used a more consistent base system., Come abbiamo detto in precedenza, i Maya usavano un sistema base-20, chiamato sistema “vigesimal”. Come il nostro sistema, è posizionale, il che significa che la posizione di un simbolo numerico indica il suo valore di posizione. Nella tabella seguente è possibile vedere il valore posto nel suo formato verticale.
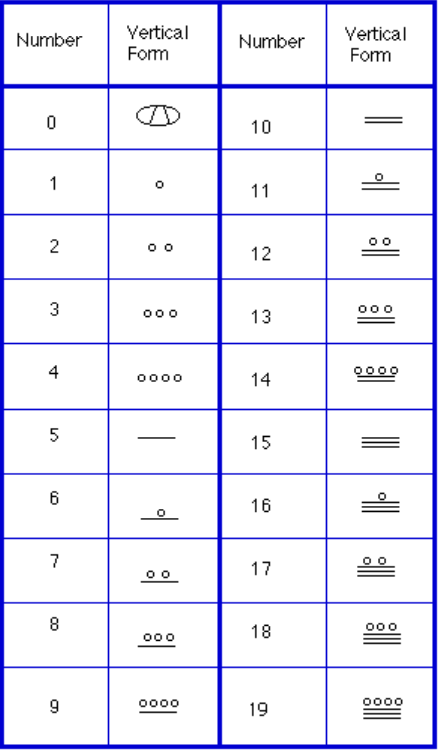
Per scrivere i numeri, c’erano solo tre simboli necessari in questo sistema. Una barra orizzontale rappresentava la quantità 5, un punto rappresentava la quantità 1 e un simbolo speciale (pensato per essere una shell) rappresentava zero., Il sistema Maya potrebbe essere stato il primo a utilizzare zero come segnaposto/numero. I primi 20 numeri sono mostrati nella tabella a destra.
A differenza del nostro sistema, dove il posto inizia a destra e poi si sposta a sinistra, i sistemi Maya posizionano quelli sul fondo di un orientamento verticale e si spostano verso l’alto man mano che il valore del posto aumenta.
Quando i numeri sono scritti in forma verticale, non ci dovrebbero mai essere più di quattro punti in un unico punto. Quando si scrivono numeri Maya, ogni gruppo di cinque punti diventa una barra., Inoltre, non ci dovrebbero mai essere più di tre barre in un unico posto-quattro barre sarebbero convertite in un punto nel punto successivo. È lo stesso di 10 che viene convertito in un 1 nel prossimo posto quando portiamo durante l’aggiunta.
Esempio
Qual è il valore di questo numero, che viene mostrato in forma verticale?
Esempio
Qual è il valore della seguente Maya numero?,
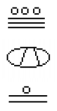
Provalo
Converti il numero Maya sottostante in base 10.,

Esempio
Convertire in base 10 numero 357510 Maya numeri.
Scrivere numeri con basi maggiori di 10
Quando la base di un numero è maggiore di 10, separare ogni “cifra” con una virgola per rendere chiara la separazione delle cifre.
Ad esempio, in base 20, per scrivere il numero corrispondente a 17 × 202 + 6 × 201 + 13 × 200, scriveremmo 17,6,1320.
Nel seguente video presentiamo altri esempi di come scrivere numeri usando numeri Maya e convertire numeri scritti in Maya per in forma di base 10.,
Il prossimo video mostra altri esempi di conversione di base 10 numeri in numeri Maya.
Aggiunta di numeri Maya
Quando si aggiungono numeri Maya insieme, adotteremo uno schema che i Maya probabilmente non hanno usato, ma che renderà la vita un po ‘ più facile per noi.
Esempio
Aggiungi, in maya, i numeri 37 e 29:

Provalo
Prova ad aggiungere 174 e 78 in Maya convertendo prima in numeri Maya e quindi lavorando interamente all’interno di quel sistema. Non aggiungere in base-ten (decimale) fino alla fine quando controlli il tuo lavoro.
Nell’ultimo video mostriamo altri esempi di aggiunta di numeri Maya.,
In questo modulo, abbiamo brevemente abbozzato lo sviluppo dei numeri e il nostro sistema di conteggio, con l’accento sulla parte “breve”. Ci sono numerose fonti di informazione e ricerca che riempiono molti volumi di libri su questo argomento. Purtroppo, non possiamo cominciare a venire vicino a coprire tutte le informazioni che è là fuori.

Abbiamo solo scalfito la superficie della ricchezza di ricerche e informazioni che esiste sullo sviluppo dei numeri e del conteggio nel corso della storia umana., Ciò che è importante notare è che il sistema che usiamo ogni giorno è un prodotto di migliaia di anni di progresso e sviluppo. Rappresenta i contributi di molte civiltà e culture. Non scende a noi dal cielo, un dono degli dei. Non è la creazione di un editore di libri di testo. È davvero umano come noi, come lo è il resto della matematica. Dietro ogni simbolo, formula e regola c’è un volto umano da trovare, o almeno da cercare.
Inoltre, ci auguriamo che ora avete un apprezzamento di base per quanto interessante e diversi sistemi numerici possono ottenere., Inoltre, siamo abbastanza sicuri che hai anche iniziato a riconoscere che diamo per scontato il nostro sistema numerico così tanto che quando proviamo ad adattarci ad altri sistemi o basi, ci troviamo veramente a dover concentrarci e pensare a cosa sta succedendo.







