Quando una frazione “normale” contiene frazioni nel numeratore o nel denominatore o in entrambi, la consideriamo una frazione complessa. Questo tipo di frazione è anche noto come frazione composta.
Esistono due metodi utilizzati per semplificare questo tipo di frazione.
Metodo 1
Passi chiave:
- Creare una singola frazione nel numeratore e denominatore.,
- Applica la regola di divisione delle frazioni moltiplicando il numeratore per il reciproco o l’inverso del denominatore.
- Semplificare, se necessario.
Metodo 2
Passi chiave:
- Trova il minimo Denominatore comune (LCD) di tutti i denominatori nelle frazioni complesse.
- Moltiplicare questo LCD al numeratore e denominatore della frazione complessa.
- Semplificare, se necessario.,
Dopo aver esaminato alcuni esempi, dovresti renderti conto che il Metodo 2 è molto meglio del Metodo 1 perché quasi sempre richiede meno passaggi per arrivare alla risposta finale.
Esempi di come semplificare frazioni complesse
Esempio 1: Semplificare la frazione complessa di seguito.
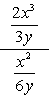
- Utilizzando il metodo 1
Sia il numeratore che il denominatore della frazione complessa sono già espressi come singole frazioni. E ‘ fantastico!,

Il prossimo passo da fare è applicare la regola di divisione moltiplicando il numeratore per il reciproco del denominatore. Finire annullando i fattori comuni per ottenere la risposta finale.
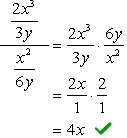
- Utilizzando il metodo 2
Trova il display LCD dell’intero problema, ovvero il display LCD dei denominatori superiore e inferiore.,

Poiché il display LCD di 3y e 6y è solo \textbf{6y}, ora moltiplicheremo il numeratore complesso e il denominatore per questo LCD. Dopo averlo fatto, possiamo aspettarci che il problema venga ridotto a una singola frazione che può essere semplificata come al solito.
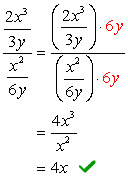
Esempio 2: Semplificare la frazione complessa di seguito.,
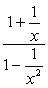
- Utilizzando il Metodo 1
In questo metodo, vogliamo creare una singola frazione sia al numeratore e al denominatore. Ovviamente, questo problema ci richiederebbe di farlo prima di eseguire la divisione.
Aggiungi le frazioni nel numeratore e sottrai quelle nel denominatore.,
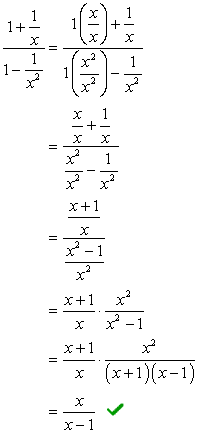
- Utilizzando il Metodo 2
Guardando i denominatori \large{x} e \large{x^2}, il suo display LCD deve essere \large{x^2} Moltiplicare la parte superiore e inferiore di questo LCD.
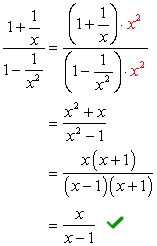
Esempio 3: Semplificare la frazione complessa di seguito.,
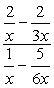
- Usando il metodo 1
Crea singole frazioni sia nel numeratore che nel denominatore, quindi segui dividendo le frazioni.
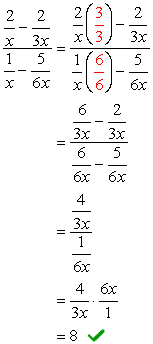
- Usando il metodo 2
L’LCD complessivo dei denominatori è \color{red}6x. Usalo per moltiplicare le espressioni superiore e inferiore.,
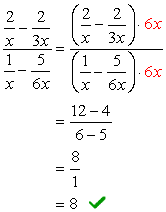
Esempio 4: Semplificare la frazione complessa di seguito.
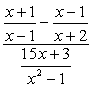
Per questo problema, useremo solo il Metodo 1.
Il problema richiede di applicare il metodo FOIL (moltiplicazione di due binomi) e una semplice fattorizzazione del trinomio. Può sembrare un po ‘ intimidatorio in un primo momento; tuttavia, se si presta attenzione ai dettagli, vi garantisco che non è poi così male.,
Se osservi, il denominatore complesso è già nella forma che vogliamo – avendo un simbolo frazionario. Ciò significa che dobbiamo lavorare un po ‘ sul numeratore complesso. Il nostro prossimo passo sarebbe quello di trasformare il numeratore complesso in una frazione “semplice” o singola.
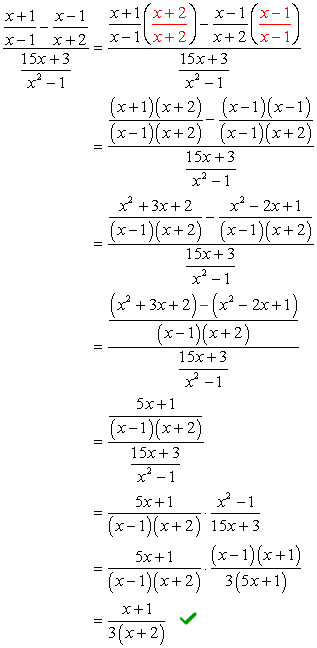
Esempio 5: Semplificare la frazione complessa di seguito.
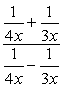
Per questo problema, useremo solo il Metodo 2.,
Osserva che il display LCD di tutti i denominatori è solo \ color {red}12x. Usalo come moltiplicatore comune per entrambe le espressioni superiore e inferiore.
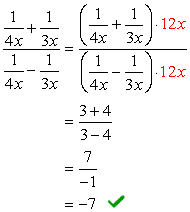
Pratica con i Fogli di lavoro
Si potrebbe anche essere interessati a:
Moltiplicare Complesso Frazioni
Dividere i Numeri Complessi