5 Clustering Algoritmer Data Forskere Trenger å Vite

jeg har nylig startet en bok-fokusert pedagogisk nyhetsbrev. Bestill Dykk er en bi-ukentlige nyhetsbrev, der for hver nye sak vi dykke inn i en non-fiction bok. Du vil lære om bokens kjerne leksjoner og hvordan man kan anvende dem i det virkelige liv. Du kan abonnere for det her.

Clustering er en Maskin Læring teknikk som innebærer gruppering av data poeng. Gitt et sett av data poeng, kan vi bruke en clustering algoritmen for å klassifisere hver data peker i en bestemt gruppe., I teorien, data punkter som er i samme gruppe skal ha lignende egenskaper og/eller funksjoner, mens data peker i forskjellige grupper bør ha svært ulike egenskaper og/eller funksjoner. Klynger er en metode for uten tilsyn læring og er en vanlig teknikk for statistisk dataanalyse som brukes på mange felt.

I Data Vitenskap, kan vi bruke clustering analyse for å få noen verdifull innsikt fra våre data ved å se hvilke grupper data poeng falle i når vi bruker en clustering algoritmen., I dag kommer vi til å se på 5 populære clustering algoritmer som data forskere trenger å vite, og deres fordeler og ulemper!

K-Betyr Clustering

K-Means er trolig den mest kjente clustering algoritmen. Det er undervist i en rekke innledende data vitenskap og maskinlæring klasser. Det er lett å forstå og implementere i koden! Sjekk ut grafikken nedenfor for en illustrasjon.,

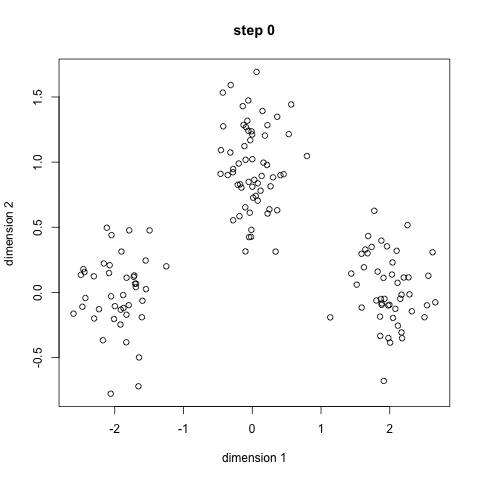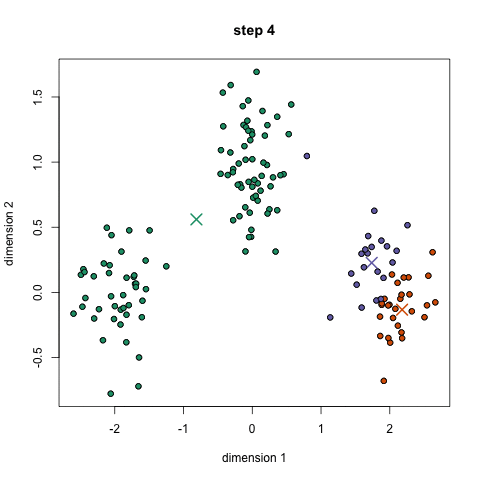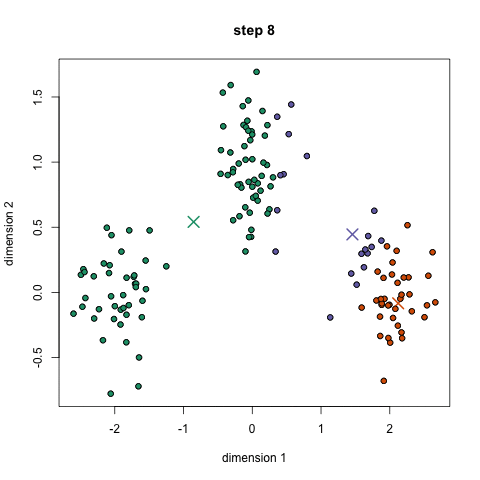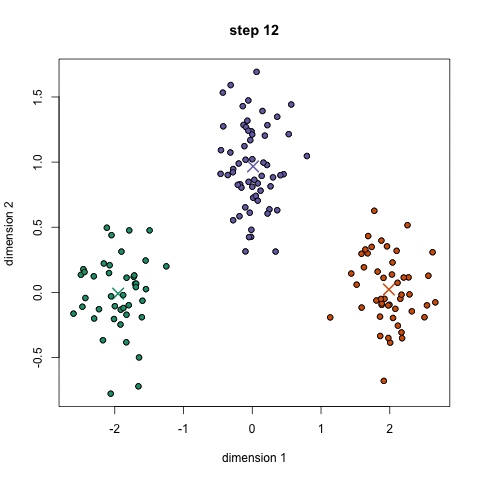
1. for Å begynne, vi velger først et antall klasser/grupper å bruke og tilfeldig initialisere sine respektive center poeng. For å finne ut antall klasser å bruke, er det godt å ta en rask titt på data, og prøve å identifisere noen forskjellige grupperinger. Sentrum poeng er vektorer av samme lengde som hvert datapunkt vektor og er «X-er» i grafisk ovenfor.,
2. Hvert datapunkt er klassifisert ved å beregne avstanden mellom punktet og hver gruppe center, og deretter klassifisere poenget å være i gruppe hvis sentrum er nærmest til det.
3. Basert på disse klassifisert poeng, vi recompute gruppen center ved å ta gjennomsnittet av alle vektorer i gruppen.
4. Gjenta disse trinnene for et angitt antall iterasjoner eller til gruppen sentre ikke endre mye mellom iterasjoner. Du kan også velge å tilfeldig initialisere gruppen sentre et par ganger, og velg deretter kjør som ser ut som det er gitt de beste resultatene.,

K-Means har den fordelen at det er ganske fort, så alt vi egentlig gjør, er å beregne avstander mellom punkter og gruppe sentre; svært få beregninger! Det er altså en lineær kompleksitet O(n).

På den annen side, K-Means har et par ulemper. For det første, du har å velge hvor mange grupper/klasser er det. Dette er ikke alltid trivielle og ideelt med en clustering algoritmen vi ønsker det å regne dem ut for oss, fordi poenget med det er å få innsikt fra data., K-means starter også med et tilfeldig utvalg av klyngen sentre og derfor kan det gi ulike klynger resultater på forskjellige kjøringer av algoritmen. Dermed kan resultatene ikke være repeterbare og manglende konsistens. Andre klynge metoder er mer konsistent.

K-Medians er en annen clustering algoritmen knyttet til K-Means, unntatt i stedet for recomputing gruppen center poeng å bruke mener vi bruke median vektor av gruppen., Denne metoden er mindre følsom for ekstreme verdier (på grunn av bruk av Medianen), men er mye langsommere for større datasett som sortering er nødvendig på hver iterasjon når computing Median vektor.

Mener-Shift Clustering

Mean shift clustering er en glidende vindu-basert algoritme som forsøker å finne tette områder av data poeng. Det er en centroid-basert algoritme som betyr at målet er å finne midten poeng i hver gruppe/klasse, som fungerer ved å oppdatere kandidater til sentrum poeng å bety av punktene i det glidende vindu., Disse kandidat windows blir deretter filtrert i en post-prosessering scenen for å eliminere nær-duplikater, danner det siste settet av center poeng og tilsvarende grupper. Sjekk ut grafikken nedenfor for en illustrasjon.

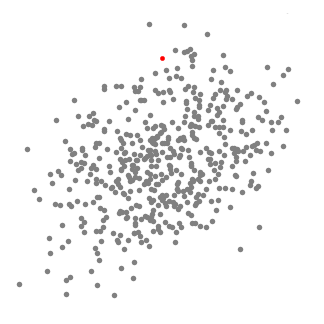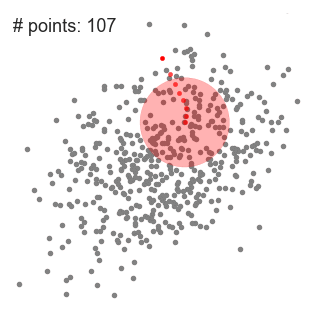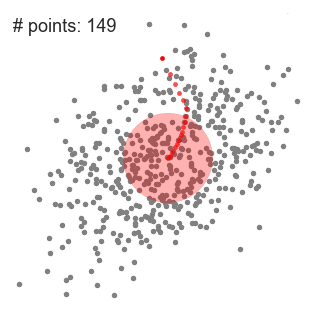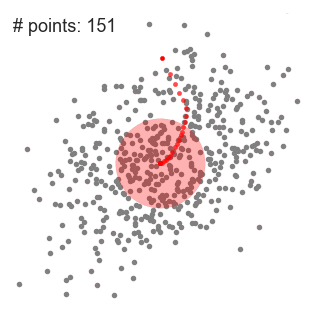
1. for Å forklare bety-shift-vi vil vurdere et sett av punkter i to-dimensjonale rommet som illustrasjonen over., Vi begynner med en sirkulær glidende vindu sentrert på et punkt C (tilfeldig valgt), og har radius r som kjernen. Mean shift er en hill-klatring algoritme som flytter denne kjernen iterativt til en høyere tetthet regionen på hvert trinn til konvergens.
2. Ved hver iterasjon, skyvevinduet er forskjøvet mot områder med høyere tetthet av skiftende midtpunktet til gjennomsnittet av punktene i vinduet (derav navnet). Tettheten innenfor glidende vindu er proporsjonal med antall poeng på innsiden., Naturlig, ved å flytte til gjennomsnittet av punktene i vinduet vil det gradvis bevege seg mot områdene med høyest tetthet.
3. Vi fortsetter å flytte skyve vinduet i henhold til bety inntil det er ingen retning på som et skifte kan romme mer poeng inne i kjernen. Sjekk ut grafikken ovenfor; vi bevege seg i sirkel til vi ikke lenger er økende tetthet (jeg.e antall poeng i vinduet).
4. Denne prosessen fra trinn 1 til 3 er gjort med mange skyve vinduer til alle punktene ligger innenfor et vindu., Når flere sliding windows overlapper vinduet som inneholder mest poeng er bevart. Dataene poeng er deretter gruppert i henhold til den glidende vindu der de bor.

En illustrasjon av hele prosessen fra ende-til-ende med alle sliding windows er vist nedenfor. Hvert svart punkt representerer centroid av en glidende vindu og hver grå prikk er en data-punkt.,

I motsetning til K-betyr clustering, det er ikke nødvendig å velge antall klynger som mener-shift automatisk oppdager dette. Det er en stor fordel. Det faktum at klyngen sentre konvergerer mot poeng av maksimal tetthet er også ganske ønskelig, som det er ganske intuitivt å forstå og passer godt i en naturlig data-drevet fornuftig., Ulempen er at utvalget av vinduet størrelse/radius «r» kan være ikke-trivielt.

Tetthet-Basert Romlig Gruppering av Programmer med Støy (DBSCAN)

DBSCAN er en tetthet-basert gruppert algoritme lignende til å bety-skift, men med et par viktige fordeler. Sjekk ut annen fancy grafikk under og la oss komme i gang!,

1. DBSCAN begynner med en vilkårlig starter data punkt som ikke har vært besøkt. Nabolaget til dette punktet er trukket ut ved hjelp av en avstand ε ε (Alle tilgangspunkter som er innenfor ε avstand er nabolaget poeng).,
2. Dersom det er et tilstrekkelig antall poeng (i henhold til minPoints) innenfor dette området så clustering prosessen starter og gjeldende data punktet blir det første punktet i den nye klyngen. Ellers punkt vil bli merket som støy (senere denne støyende punktet kan bli en del av klyngen). I begge tilfeller er det punktet som er merket som «besøkt».
3. For dette første punktet i den nye klyngen poeng i sin ε avstand nabolaget også bli en del av den samme klynge., Denne prosedyren for å lage alle punkter i ε-området, tilhører den samme klyngen er deretter gjentas for alle de nye punkter som har vært bare lagt til klyngen gruppe.
4. Denne prosessen i trinn 2 og 3 er gjentatt til alle punkter i klyngen er fastsatt jeg.e alle punktene i det ε-området i klyngen har blitt besøkt og merket.
5. Når vi er ferdig med dagens cluster, en ny ubenyttede punktet er hentet og behandlet, noe som fører til oppdagelsen av et ytterligere klynge eller støy. Denne prosessen gjentas inntil alle punktene markeres dette som besøkt., Siden slutten av dette alle punkter har blitt besøkt hvert punkt har blitt merket som enten tilhøre en klynge eller blir støy.

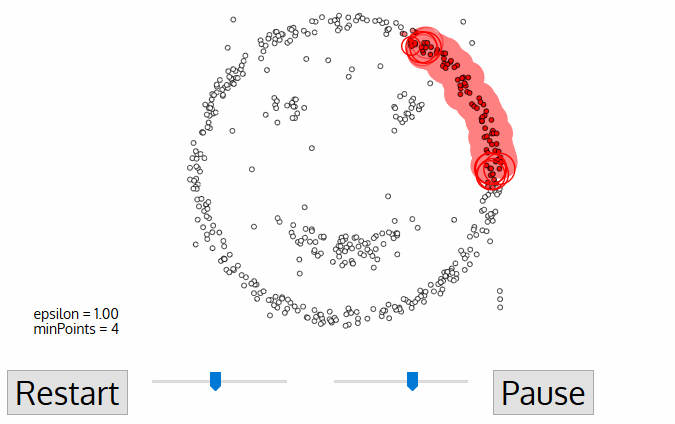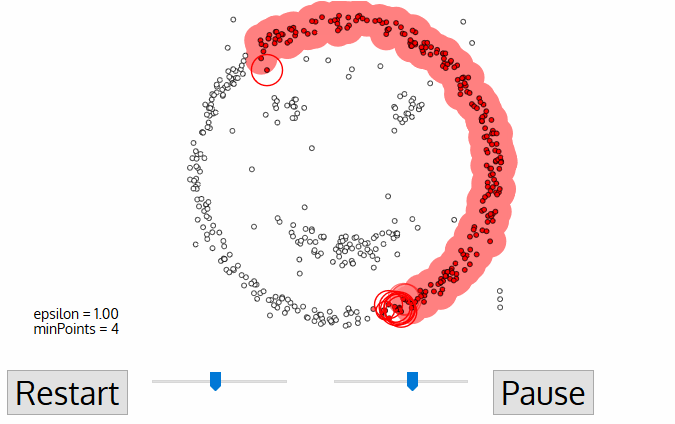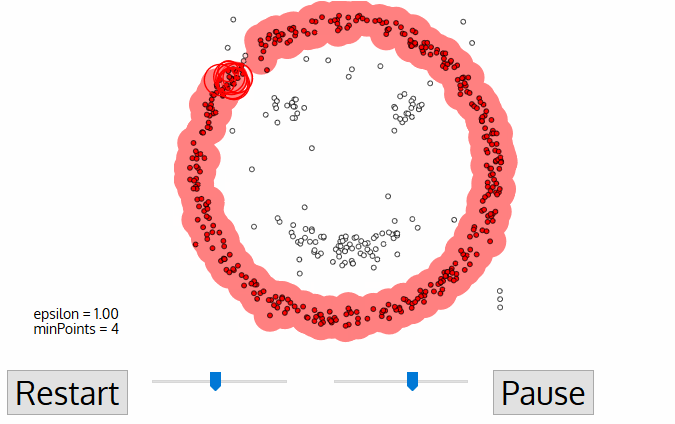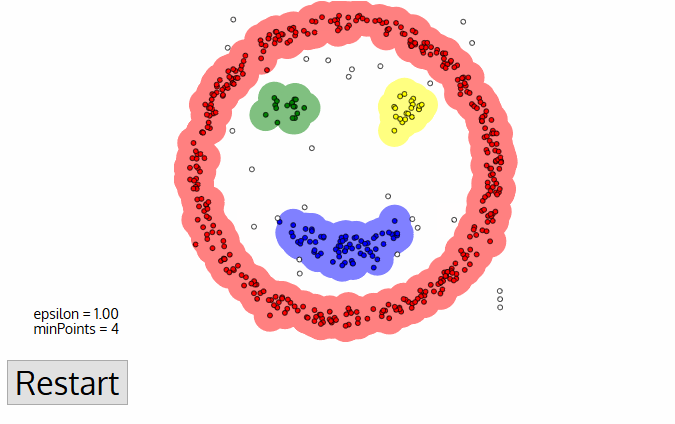
DBSCAN utgjør noen store fordeler over andre clustering algoritmer. For det første, krever det ikke en pe-angi antall klynger i det hele tatt. Det identifiserer også uteliggere som lyder, i motsetning til mener-shift-som rett og slett kaster dem inn i en klynge selv om data punktet er veldig forskjellige. I tillegg kan det finne vilkårlig størrelse og vilkårlig formet klynger ganske godt.,

Den største ulempen av DBSCAN er at det ikke utføre så vel som andre når klyngene er av varierende tetthet. Dette er fordi innstillingen av avstanden terskelen ε og minPoints for å identifisere nabolaget poeng vil variere fra klyngen for å klynge når tettheten varierer. Denne ulempen oppstår også med svært høy-dimensjonale data siden igjen avstanden terskelen ε blir det vanskelig å anslå.,

Forventning–Maksimering (EM) Clustering ved hjelp av Gauss Blanding Modeller (GMM)

En av de store ulempene med K-Means er sin naive bruk av middelverdien for klyngen center. Vi kan se hvorfor dette er ikke den beste måten å gjøre ting på, ved å se på bildet nedenfor. På venstre side, det ser ganske opplagt for det menneskelige øyet at det er to runde klynger med forskjellig radius’ sentrert på samme mener. K-Betyr ikke kan håndtere dette fordi de mener verdier av klyngene er veldig tett sammen., K-Betyr heller ikke i tilfeller der klynger ikke er sirkulær, igjen som et resultat av å bruke det betyr som klynge center.

Gaussian Blanding Modeller (GMMs) gi oss mer fleksibilitet enn K-Means. Med GMMs vi antar at dataene poeng er Gaussisk fordelt; dette er en mindre restriktiv antagelse enn å si at de er forbundet ved hjelp av gjennomsnittet., På den måten, vi har to parametre for å beskrive formen på klynger: gjennomsnitt og standardavvik! Å ta et eksempel i to dimensjoner, dette betyr at klynger kan ta noen form for elliptisk form (siden vi har et standardavvik i både x-og y retninger). Dermed, hver Gaussiske fordelingen er tilordnet til en enkelt klynge.

for Å finne parametrene til den Gaussiske for hver klynge (e.g middelverdi og standardavvik), vil vi bruke en optimalisering algoritme kalt Forventning–Maksimering (EM)., Ta en titt på diagrammet nedenfor som en illustrasjon av Gaussians være montert til klynger. Da kan vi gå videre med prosessen av Forventning–Maksimering clustering ved hjelp av GMMs.

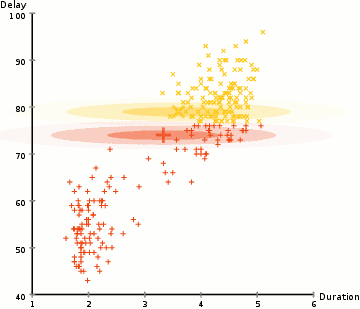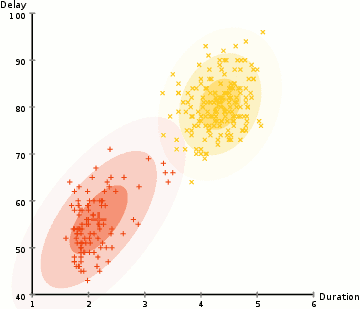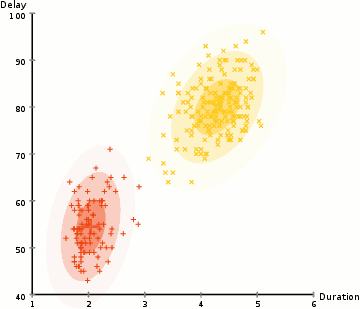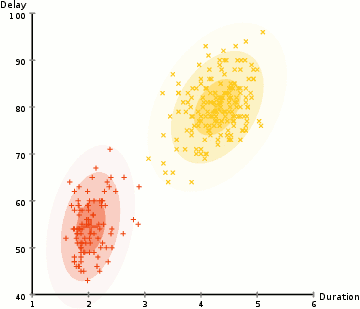
1. Vi begynner med å velge antall klynger (som K-Betyr) og tilfeldig initialiserer den Gaussiske fordelingen parametere for hver klynge., Man kan prøve å gi en god guesstimate for første parametere ved å ta en rask titt på data for. Men merk, som kan sees i grafisk ovenfor, dette er ikke 100% nødvendig som Gaussians starte vår som svært dårlig, men er raskt optimalisert.
2. Gitt disse Gaussiske fordelinger for hver klynge, beregne sannsynligheten for at hvert datapunkt tilhører en bestemt klynge. Jo nærmere en er å være den Gaussiske sentrum, jo mer sannsynlig er det hører til at klyngen., Dette bør gjøre intuitiv følelse siden med en Gaussisk fordeling vi antar at de fleste av de data som ligger nærmere midten av klyngen.
3. Basert på disse sannsynlighetene, vi beregner et nytt sett av parametere for den Gaussiske fordelinger, slik at vi maksimere sannsynligheten av data poeng i klynger. Vi beregne disse nye parametere ved hjelp av en vektet sum av data punktet posisjoner, der vektene er sannsynlighetene av data viser at tilhørighet i en bestemt klynge., For å forklare dette visuelt vi kan ta en titt på den grafiske ovenfor, spesielt den gule klynge som et eksempel. Fordelingen starter tilfeldig på den første utgaven, men vi kan se at de fleste av de gule punktene er til høyre for at distribusjon. Når vi beregne en vektet sum av sannsynligheter, selv om det er noen punkter nær sentrum, de fleste av dem er på høyre side. Dermed naturlig fordelingen er slem er flyttet nærmere de sett av punkter. Vi kan også se at de fleste av punktene er «øverste høyre til nederste venstre»., Derfor er standardavviket endringer for å opprette en ellipse som er mer tilpasset til disse punktene, for å maksimere summen vektet av sannsynligheter.
4. Trinn 2 og 3 er gjentatt iterativt til konvergens, hvor fordelingen ikke endre seg mye fra utgave til utgave.

Det er 2 viktige fordeler med å bruke GMMs. For det første GMMs er en mye mer fleksibel i forhold til klyngen covariance enn K-Means; på grunn av den standardavvik parameteren, klynger kan ta på noen ellipse form, snarere enn å være begrenset til sirkler., K-Means er faktisk et spesielt tilfelle av GMM i hver klynge er covariance langs alle dimensjoner tilnærminger 0. For det andre, siden GMMs bruke sannsynligheter, kan de ha flere klynger per datapunkt. Så hvis et datapunkt er i midten av to overlappende klynger, vi kan bare definere sin klasse ved å si det tilhører X-prosent til klasse 1 og Y-prosent til klasse 2. I. e GMMs støtte blandet medlemskap.

Agglomerative Hierarkisk Klynging

Hierarkisk klynging algoritmer falle inn i 2 kategorier: top-down eller bottom-up., Nedenfra-og-opp algoritmer behandle hvert datapunkt som en enkelt klynge i begynnelsen og deretter suksessivt flette (eller klumpe) par klynger til alle klynger har blitt slått sammen til en enkelt klynge som inneholder alle data poeng. Nedenfra-og-opp hierarkisk klynging kalles derfor hierarkisk agglomerative clustering eller HKS. Dette hierarki av grupper er representert som et tre (eller dendrogram). Roten av treet er den unike klynge som samler alle prøvene, bladene blir klynger med bare ett eksempel., Sjekk ut grafikken nedenfor finner du en illustrasjon før du går videre til algoritmen trinn

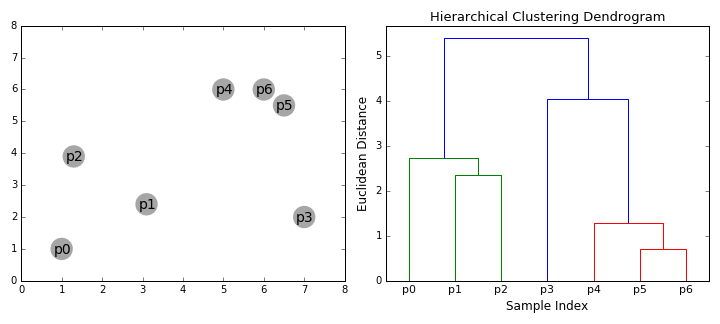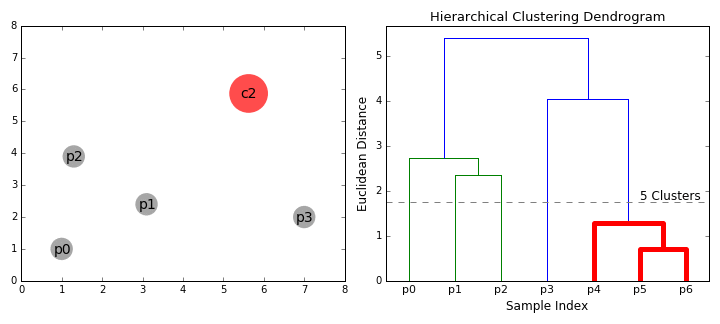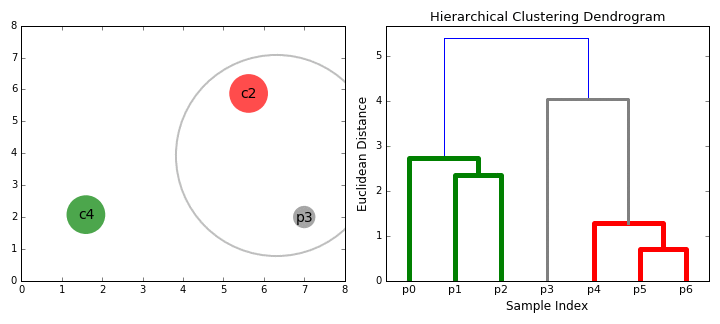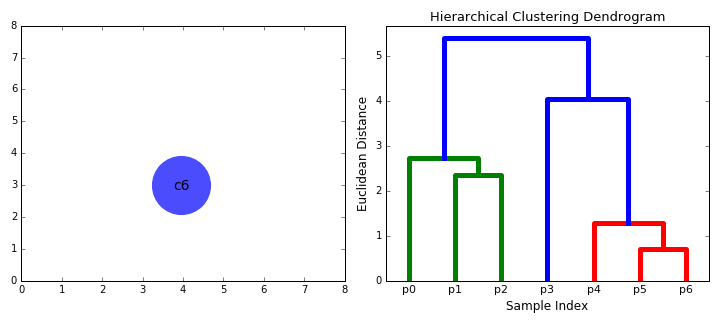
begynner Vi ved å behandle hvert datapunkt som en enkelt klynge jeg.e hvis det er X-data poeng i vårt datasett har vi X klynger. Så vi velger en avstand beregning som måler avstanden mellom to klynger., Som et eksempel, vil vi bruke en gjennomsnittlig sammenhengen som definerer avstanden mellom to klynger for å bli den gjennomsnittlige avstanden mellom datapunkter i den første klyngen og data poeng i den andre klyngen.

På hver iterasjon, vi kombinerer to samlinger i ett. De to klynger for å bli kombinert er valgt som de med de minste gjennomsnittlige sammenhengen. I. e i henhold til våre utvalgte avstand beregning, er det disse to klynger har den minste avstanden mellom hver andre og derfor er den som er mest lik og bør kombineres.

Trinn 2 gjentas til vi kommer roten av treet jeg.,e vi bare har én klynge som inneholder alle data poeng. På denne måten kan vi velge hvor mange klynger vi vil i slutten, bare ved å velge når du skal stoppe å kombinere klynger jeg.e når vi slutter å bygge treet!

Hierarkisk klynging ikke krever oss til å angi antall klynger og vi kan selv velge hvilket antall klynger ser best ut siden vi bygger et tre. I tillegg algoritmen er ikke følsomme for valg av avstand beregning; alle av dem har en tendens til å arbeide like godt mens med andre klynger algoritmer, valg av avstand beregning er kritisk., Et særlig godt eksempel på bruk av hierarkisk klynging metoder er når de underliggende data som har en hierarkisk struktur, og du ønsker å gjenopprette hierarkiet; andre clustering algoritmer kan ikke gjøre dette. Disse fordeler av hierarkisk klynging komme på bekostning av lavere effektivitet, som det har en tid kompleksitet O(n3), i motsetning til den lineære kompleksiteten av K-Means-og GMM.