– Distribusjoner
kjernespørsmålet i hjertet av problemene med Dirac delta og lignende
matematiske objekter er problemet med differentiability. Som Dirac er angitt i sitatet ovenfor, kan du ikke virkelig kjøre på problemer hvis du bruker hans δ-funksjonen som en symbolsk regel for hvordan det fungerer på andre funksjoner, men han fortsetter å differensiere δ i sine beregninger, og dette er hvor problemene virkelig begynner., Hvordan kan man vite a priori «når disse operasjonene er tillatt» når man ikke selv har en fast definisjon av objekter, eller hva det ville si å skille dem? Vi vil se på hvordan disse spørsmålene føre til avledning av nye og strengt definert matematiske objekter.
Functionals
Vurdere hvordan en normalt bestemmer derivatet (eller antiderivative) til en funksjon. Under normale omstendigheter, med «klassisk» – funksjonene, du har en godt definert regel som beskriver hvordan en funksjon maps ett sett av reelle tall til et annet sett, sier f : ℝ →ℝ., Gitt dette, og definisjonene av integrert eller derivat, da kan man tydelig undersøke de verdier som disse operatørene avkastning når den brukes til funksjonen. I tilfelle av δ, vi har ingen brukbar definisjon for å gå videre langs disse linjene. I stedet, i praksis δ er tydeligst definert av hvordan den virker på andre, godt definerte funksjoner (som i (3)). Dette er viktig innsikt som fører til den moderne teori for distribusjoner. Det viser seg at den riktige måten å behandle matematisk δ, og en stor klasse av lignende objekter, er å slutte å prøve å definere dem som funksjoner i det hele tatt., Denne tankegangen er godt beskrevet av Jean Dieudonne i sin anmeldelse av (se ):
… man starter med en familie med veldig «vanlig» funksjoner (vanligvis med
med hensyn til ulike egenskaper), som tilfredsstiller visse (vanligvis
integrert) relasjoner, eller som enkelte operasjoner er mulig; og
da man oppdager at en a priori større familie av funksjoner tilfredsstiller
det samme forholdet, eller kan bli utsatt for lignende virksomhet. Mange
spørsmål da kan naturligvis bli spurt: Er dette nye familie virkelig
forskjellig fra den første?, Hvis den er det, hva er forholdet mellom
to familier, og kan gi en presis beskrivelse av den nye?
Det er først i den siste fasen av «forhistorie» at det kan være
kalles en revolusjonerende synspunkt vil dukke opp, med ideen om at
«ny familie» kan bestå av andre objekter enn funksjoner.
Den andre objekter antydet er functionals. Du kan tenke på en funksjonell
som en funksjon av funksjoner., Som en funksjon er en unik mapping fra ett sett av
nummer til en annen, en funksjonell F kan defineres som en kartlegging F : C →ℝ,
der C er noen sett av funksjoner. Som er en funksjonell kart funksjoner til ekte
tall., Et enkelt eksempel på en funksjonell av denne typen er den bestemte integral:

noe som helt klart tar en funksjon f fra noen sett på tilstrekkelig integrable funksjoner og kart det til et reelt tall, verdien av integralet, eller området under kurven f(x) mellom a og b. Dette er bare ett eksempel., En kan tenke seg et uendelig antall functionals, og setter av functionals; man kan til og med fortsette å generalisere og definere tilordninger fra sett av functionals til reelle tall. Det er verken her eller der. Hva er viktig er at den funksjonelle konseptet kan brukes til å definere distribusjoner.
Det Sett av Test Funksjoner
Vi trenger en mer definisjon for å oppnå våre mål. Dette beløp med å spesifisere set C av funksjoner som distribusjoner vil kartet funksjoner til reelle tall., Funksjoner er ofte samlet i sett som spesifiserer deres grad av kontinuitet, differentiability, og kontinuiteten i deres derivater. Vi sier at en funksjon f er i settet C⁰ (skrive f ∈ C⁰) hvis det er kontinuerlig over hele ekte linje, i den forstand at grensen på alle punkter er det samme når de er tatt fra venstre eller høyre; det er ikke nødvendigvis differensiable. Vi sier at f ∈ C1 hvis dens deriverte eksisterer og er kontinuerlig, dvs. f ‘ ∈ C⁰. For eksempel, den funksjonen g(x) = |x| er kontinuerlig, men ikke differensiable ved x= 0; g er i C⁰ men ikke i C1., Vi kan generalisere dette og si at Cⁿ er sett av funksjoner som har for kontinuerlige funksjoner deres første n derivater, der n er et heltall.
Som n blir større, sett blir på en måte «mindre;» du kan alltid finne funksjoner (uendelig mange!) som er i Cⁿ men ikke Cⁿ⁺1. Disse «kontinuitet spaces» derfor danne en sekvens av nestede undergrupper, som vist nedenfor.

Nær bunnen av denne uendelig sekvens av sett av funksjoner finner vi set
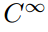
som selvfølgelig sett alle funksjoner som har uendelig mange kontinuerlig derivater. Mange kjente og vennlige funksjoner er i denne siste klassen (for eksempel sin(x), cos(x); eˣ; alle polynomer)., Disse funksjonene kalles «glatt» eller «oppførte seg bra» fordi man kan utføre operasjonen av differensiering på dem så mange ganger man vil, uten å bekymre. Men selv om dette sikkert har uendelig mange medlemmer, de er sjeldne i den forstand at de fleste funksjoner er ikke så oppførte seg bra.
angi som er egnet for definisjon av inntekt er enda mindre
enn dette. Det krever en ekstra kriterium: at funksjoner har kompakt support. Denne tekniske uttrykket betyr ganske enkelt at en funksjon har verdier som ikke er null innenfor et bestemt domene, og er jevnt null utenfor dette., Vi vil derfor bruke notasjonen
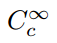
for å betegne den sett av uendelig kontinuerlig differensiable funksjoner med kompakt support, og kaller slike funksjoner teste funksjoner. For å definere en klasse for functionals ved hjelp av dette settet som et domene, bør vi være sikker på at det faktisk er medlemmer av dette settet., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

Definisjon
Fra dette punktet definisjonen av en distribusjon er grei. En distribusjon er en lineær funksjonelle
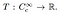
Det er det er en mapping fra settet med tester funksjonene til et reelt tall. Analogt til hvordan en bestemt funksjon fungerer på en inngang nummer, og produserer en effekt, bestemte utdelinger er definert av hvordan de forvandle teste funksjoner til tall., Fordelingen skuespill av test-funksjonen φ kan skrives som T (φ), eller vanlig som〈T,φ〉.
En kan nå se hvorfor utdelinger er kalt generaliserte funksjoner. For noen
klassisk funksjon som integrert

er godt definert, det er en tilsvarende fordeling F slik at 〈F,φ〉gir verdien av dette integrert., Det er imidlertid også distribusjoner som ikke stemmer overens med klassisk funksjoner; – distribusjoner er mer generelle. Som bør være klart nå, den kanoniske eksempel på en fordeling som ikke samsvarer med en klassisk funksjon er Dirac δ., Vi vil derfor til slutt kommer til et fullt streng definisjon av δ som distribusjon slik at

Generalisert eller «Svake» Derivative
δ distribusjon er bare en av uendelig mange distribusjoner som ikke
svarer til klassiske funksjoner. Vi kan få noen flere av disse ved å skille δ i den forstand av fordelinger., Men hvordan gjør du det konseptet med en
distribusjon løse problemet med differensiering som diskutert tidligere? Vi trenger bare generalisere begrepet differensiering skal gjelde for utdelinger.
Vurdere en funksjon f ∈ C1, slik at det er kontinuerlig differensiable. Beregning ved hjelp av integrering av deler, vi ser at

Uttrykket i parentes forsvinner siden φ, som en test funksjonen, har kompakt support., Dette generaliserer til en distribusjon, sier F’, som svarer til funksjonen f’:

Denne beregningen generaliserer ganske enkelt å distribusjoner som ikke svarer til en klassisk funksjonen f., På denne måten kan vi definere den avledede T’ T, i den forstand distribusjoner:

Dette er også noen ganger referert til som den svake deriverte, siden den strekker seg derivater funksjoner som normalt ikke ville være differensiable. Dette generaliserer enda lenger, til høyere for derivater., Vi kan definere den n-te deriverte av en fordeling T som T⁽ⁿ⁾, der sistnevnte er fordelingen slik at

Her
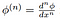
er den klassiske derivat av test-funksjonen, som er sikret
for å eksistere ved selve definisjonen av test funksjoner!, Det følger av dette at alle utdelinger er uendelig differensiable (i den forstand av fordelinger).
Dette fjerner fullstendig kampen som Dirac og andre står overfor når differensiere δ-funksjonen. Etter det vi har definert her, et derivat av δ bare sifts for verdien av en annen funksjoner derivat på null., Formelt,

Dette gir en stringent matematisk rammeverk for derivater av δ som dukket opp i litteraturen lenge før denne teorien kom inn i eksistens.
Det finnes en rekke andre operasjoner som gjelder for funksjoner som har blitt generalisert til å gjelde for utdelinger. De kan bli lagt til og trukket fra, convolved, og forvandlet ved hjelp av Laplace og Fourier-transformasjoner., Det er imidlertid umulig å definere multiplikasjon av fordelinger på en måte som bevarer algebra som gjelder for klassisk fungerer (Schwartz Umulighet Teorem).