Når en «normal» brøkdel inneholder fraksjoner i enten telleren eller nevneren eller begge, så vi anser det å være en komplisert brøkdel. Denne type fraksjon, også kjent som en sammensatt brøkdel.
Det er to metoder som brukes til å forenkle en slik type brøkdel.
Metode 1
– Tasten fremgangsmåte:
- Opprett en enkelt fraksjon i teller og nevner.,
- Bruk divisjon regel av brøker ved å multiplisere teller med gjensidige eller inverse av nevneren.
- Forenkle, hvis det er nødvendig.
Metode 2
– Tasten fremgangsmåte:
- Finn Minste Felles Multiplum (LCD) av alle denominators i komplekse fraksjoner.
- Multiplisere denne LCD-skjermen for å telleren og nevneren av komplekse brøkdel.
- Forenkle, hvis det er nødvendig.,
Etter å ha gått over et par eksempler, bør du innse at Metode 2 er mye bedre enn Metode 1 fordi nesten alltid det tar færre trinn for å få til den endelige svar.
Eksempler på Hvordan å Forenkle Komplekse Fraksjoner
Eksempel 1: Forenkle komplekse brøkdel nedenfor.
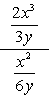
- ved Hjelp av Metode 1
Både telleren og nevneren av komplekse brøkdel er allerede uttrykt som enkelt fraksjoner. Dette er flott!,

neste trinn å gjøre er å søke divisjon regel ved å multiplisere teller med gjensidige i nevneren. Avslutt med å kansellere ut felles faktorer for å få det endelige svaret.
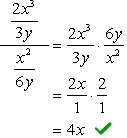
- ved Hjelp av Metode 2
Finn en LCD-av hele problemet, det er, LCD-på toppen og bunnen denominators.,

Siden LCD-3y og 6y er bare en \textbf{6y}, vil vi nå må du multiplisere den komplekse teller og nevner med denne LCD-skjermen. Etter du har gjort dette, kan vi forvente at problemet reduseres til en enkelt fraksjon som kan forenkles som vanlig.
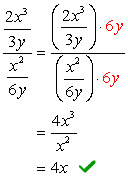
Eksempel 2: Forenkle komplekse brøkdel nedenfor.,
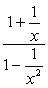
- ved Hjelp av Metode 1
I denne metoden, vi ønsker å skape et enkelt brøkdel både i teller og nevner. Det er åpenbart at dette problemet ville kreve oss til å gjøre det først, før vi utføre divisjon.
Legg til fraksjoner i telleren, og trekker de i nevneren.,
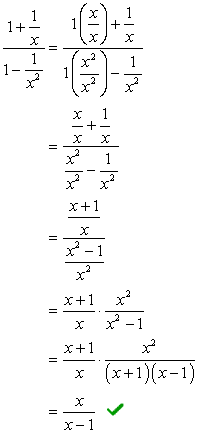
- ved Hjelp av Metode 2
Ser på denominators \large{x} og \large{x^2}, LCD-må være \large{x^2} Multiplisere toppen og bunnen av denne LCD-skjermen.
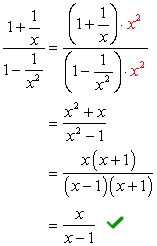
Eksempel 3: Forenkle komplekse brøkdel nedenfor.,
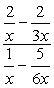
- ved Hjelp av Metode 1
Lag enkle brøker i både teller og nevner, og følg deretter ved å dividere brøker.
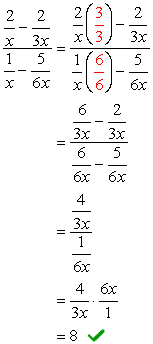
- ved Hjelp av Metode 2
Den samlede LCD-av denominators er \color{red}6x. Bruk denne til å formere seg gjennom toppen og bunnen uttrykk.,
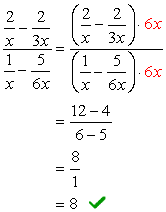
Eksempel 4: Forenkle komplekse brøkdel nedenfor.
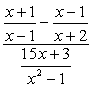
For dette problemet, og vi kommer til å bruke Metode 1.
problemet krever at du å bruke FOLIE metode (multiplikasjon av to binomials) og en enkel primtallsfaktorisering av trinomial. Det kan se litt skremmende i begynnelsen, men hvis du betaler oppmerksomhet til detaljer, jeg kan garantere deg at det er ikke så ille.,
Hvis du observerer, komplekse nevneren er allerede i den form som vi ønsker – å ha en brøk symbolet. Dette betyr at vi må jobbe litt på komplekse teller. Vårt neste skritt ville være å forvandle den komplekse teller inn i en «enkel» eller enkel brøk.
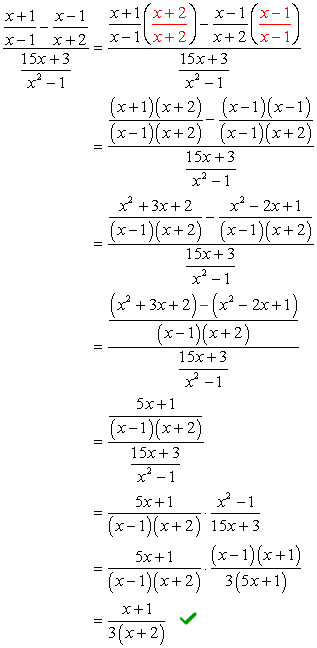
Eksempel 5: Forenkle komplekse brøkdel nedenfor.
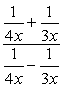
For dette problemet, og vi kommer til å bruke Metode 2.,
vær Oppmerksom på at LCD-skjermen av alle denominators er bare \color{red}12x. Bruk dette som felles multiplikator for både topp og bunn uttrykk.
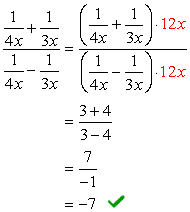
Praksis med Regneark
Du kan også være interessert i:
å Multiplisere Komplekse Fraksjoner
å Dele Komplekse Tall