For elektromagnetisme alt du trenger å vite er hva som skjer når du har + eller – kostnader, hva skjer når de kommer nær og hva som skjer når de beveger seg. Det er det! For alle ikke-quantum EM det er bare 5 formler du trenger.,den Lorentz ligningen beskriver alle av elektrisitet, magnetisme, lys, lyd, stråling, faktisk de fleste av fysikk:
(1) 
(2) 
(3) 
(4) 
(5) 
Hvor ille kan et emne bli hvis du kan beskrive det hele med bare 5 ligninger, kan du sannsynligvis passe dem alle på baksiden av en beermat., Nå som du har sett den konklusjon kan vi gå til begynnelsen og les hele historien i detalj. Med mindre du gjør et universitet kurset kan du komme unna med ikke å vite nøyaktig hva ligningen mener eller gjør, men dette området vil forklare dem senere, først lar komme tilbake til det grunnleggende.
De Grunnleggende
Kostnad kommer i 2 typer, positive og negative, og måles i Coulombs (C). Hvis du har en kostnad på egen hånd, det sender ut et felt i alle retninger. Feltet fra en kostnad er representert ved E som i Elektrisitet., Hvis du putter en kostnad i feltet det opplever en styrke. Like ladninger frastøter og i motsetning til ladninger tiltrekker. Jo større lade sterkere kraft og lenger unna kostnader svakere styrke, akkurat hva du ville forvente. Dette forholdet kan være representert av Coulombs Lov;
og
‘s er de to gebyrer og 
er avstanden mellom dem squared., Den andre biten er bare en konstant som omtrent tilsvarer 9000000000. (Den nøyaktige opprinnelsen av denne loven kan bli funnet her). Fra disse kan du se at styrken er bare feltet ganger av hvilken lader du putter i, 
. Ved hjelp av denne kan du trene felt, eller tvinge mellom partikler eller atomer eller noe med betaling, forutsatt at de ikke er i bevegelse. Når du starter en kostnad flytte andre ting til å skje.
Ting i Bevegelse
Så snart en kostnad begynner å bevege den produserer et annet felt., Det nye feltet er magnetisme og er representert ved B som i B-magmatism?
grunnen til At det er B er rett og slett at det var andre ting i en alfabetisk liste:
- Elektromagnetisk vektor potensial: A
- Magnetisk induksjon: B
- Totalt elektrisk strøm: C
- Elektrisk vekt: D
- Electromotive force: E
- Mekanisk kraft: F
- Hastighet på et punkt: G
- Magnetisk intensitet: H
(Dette forklarer også hvor H kommer fra for de som er interessert).,
Så nå dine partikkel-eller atom-eller hva har 2 felt kommer ut. Full ligningen for å beskrive hvordan begge feltene handle på en partikkel er
som er kjent som Lorentz kraft. 
symbolet ikke betegne multiplikasjon, i denne sammenheng betyr det at Cross-Produkt. Det er i utgangspunktet en kort måte å skrive «
ganger 
ganger sinus til vinkelen mellom»., Dette er fordi – feltet presser på 90° som noen gang sin retning peker OG hvilke retning du beveger deg i. Nå, med mindre du gjør EM tidligere A-nivå kan du glemme alt om retninger og vinkler og bare skrive
Hvis vi utvider ut over uttrykket vi har
Men vi kan allerede beskrive en av disse biter, 
er bare Coulombs Lov., Også, på Et nivå over eller under den situasjonen vil trolig være forenklet, slik at du bare trenger å vurdere. 
og felt separat., Så vil du sannsynligvis bare å bruke én av følgende to formler,
Tydeligvis 
er den kraft og er kostnader, og er de to feltene er beskrevet tidligere, og er hastigheten på bevegelige kostnad., Den elektriske felt måles i SI-enheter av Newtons per coulomb (
) eller tilsvarende volt per meter (
). Det magnetiske feltet har SI-enheter av Teslas (T), tilsvarende Webers per kvadratmeter (
) eller volt sekunder per kvadratmeter (
)
Kretser
Nå er jeg ikke en stor fan av kretser, aldri har vært, nå forhåpentligvis vil jeg være profesjonell nok til at min disliking av dem vil ikke komme over i denne delen, men hvis det gjør jeg beklager på forhånd., Hvis jeg virkelig begynner å slite med min hater jeg kan ha til å ringe i en annen forfatter
En kretsene er i utgangspunktet bare en serie av bevegelige kostnader, med enkelte objekt eller enhet i den måten som påvirker flyten. Nå når jeg sier at elektronene beveger seg rundt de fleste mennesker tror at deres fart rundt på nær lysets hastighet, men dette er feil. Den faktiske elektroner beveger seg SVÆRT sakte, det er den bølge som reiser raskt. Som nevnt ovenfor like ladninger frastøter, så sette ett elektron ved siden av en annen, og de vil flytte fra hverandre., Med en strøm i en ledning du i utgangspunktet har et rør av elektroner, og du skal legge til en-til-en av endene, fører dette til neste electron å flytte ned som i sin tur presset den neste og så videre. Så du har en Meksikansk bølge lignende effekt som beveger seg raskt, men elektronene seg selv er bare beveger seg sakte.
Kretser vanligvis inneholde alle slags forskjellige objekter og enheter avhengig av hva de er for, og avhengig av hvordan du har satt dem opp i kretsen avhenger av hvordan du gjør alle beregninger.
Som er Der?,
Hvis du har satt opp alle dine komponent i en lukket sløyfe som så
så sier vi at alle komponenter er i Serien. Hvis du konfigurere dem med forgrening stier som så
så sier vi at komponenter som er Parallelle. Du kan også lage kretser som er en blanding av serie-og parallell-delen som så
Ampere, Volt og Ohm (Oh my!,)
Vi kaller den bevegelige kostnader Gjeldende, og det er målt i SI-enhet for Ampere (A). Forsterkere er tilsvarende mengden av kostnad gått i en viss tid, så 2 coulombs i 6 sekunder vil være tilsvarende 0.3 A. Dette, som de fleste ting i fysikk kan være uttrykt i en fin formel for deg å lære
en Annen viktig idé i kretser er Spenning eller Potensiell Forskjell. Volt er i utgangspunktet forskjellen i Elektrisk potensial på to forskjellige punkter., Det elektriske potensialet mellom 2 poeng blir gitt som
der 
er avstanden mellom 
og 
. Det er i utgangspunktet feltet times avstand.
en Annen viktig idé når det kommer til kretser er motstand. Motstanden er i utgangspunktet et mål på hvor mye motstand mot elektrisk strøm., Nesten alle objekter eller enheter i en krets føre til motstand og til å beregne den totale resistansen i kretsen kan du bruke én eller flere av disse reglene
En av de viktigste og mest fundamentale ligninger i kretser er Ohms lov, og det gjelder strøm, spenning og motstand.
Den Dype Enden
Dette er det. Klassisk EM går ikke dypere enn dette., Disse 4 er den grunnleggende ligningen for ALLE felt i EM. De kan ta litt å få hodet rundt, men når du gjør det bør alle gjøre forstand, på en måte.,
Hvis du ikke vet om integrering og differensiering jeg foreslår at du leder over til Integrering delen eller Differensiering delen, vil jeg prøve å forklare det her, men jeg vil i hovedsak være fokus på fysikk.
Gauss’ Lov
Ok da først opp, har vi Gauss’ Lov.,
Dette sier at integralet av det Elektriske feltet, , gjennom et lukket område 
er lik den totale kostnad inne på området, 
delt av 
. er en konstant som kalles Permittivity Ledig Plass, og viser opp over fysikk sammen med 
som er Permeabilitet av Ledig Plass., Hva denne ligningen betyr er at du kan ta en lukket overflaten du liker og finne – feltet går gjennom, forutsatt at du kan gjøre matematikk. Vanligvis kan du ikke. Men det er en rekke tilfeller når det er fint og lett. Tilfeller når – feltet kommer rett ut gjennom overflaten jevnt., Sakene
- En Sfærisk overflate rundt et punkt, eller sfære
- En Sylindriske overflaten rundt en uendelig wire
- En Vanlig overflaten over en del av et uendelig plan
jeg innrømme disse høres vagt og abstrakt, så jeg vil demonstrere ved hjelp av et diagram.
Dette er den Gaussiske overflater., I utgangspunktet med disse overflatene alle du prøver å gjøre er å gjøre livet enklere. Du bare sørg for at overflaten er alltid det samme avstand fra lade kilde, og at feltet er alltid gå gjennom på 90 grader. Du kan da jobbe ut integrert med øynene lukket så enkelt er det. Venstre side av Gauss’ lov blir E ganger overflaten av den formen du har valgt.
- En Sfærisk overflate blir
, der 
er radius i den sfære., - En Sylindriske overflaten blir
, der og er lengde og radius av sylinderen. - En Vanlig overflate blir
, der 
er Området over og under uendelig overflaten (du trenger faktor på 2 som felt går over og under overflaten på 90 grader).,
So Gauss’ law for a sphere becomes
Which was introduces earlier as Coulombs Law, now you know where it came from., Gauss’ Lov for en uendelig linje av kostnad er bare
Nå i dette noe nytt har blitt introdusert, 
. Hvis du har en uendelig linje av lade den totale belastningen på det er uendelige og det er ingen måte å vite hvor mye av denne uendelig lade du ville ha inni gaussian overflaten., Det er der kommer i, er en verdi kostnad pr. enhet lengde, så hvis =4Cm
og du har 5 meter og deretter lade er bare 20C. Det er alt er bare en verdi på lade.
For et uendelig overflate gauss’ lov blir
igjen på et nytt symbol som har blitt lagt til, men det er akkurat som før., 
er bare kostnad per arealenhet, så hvis =5Cm
og du har en 100m
området den totale kostnad er 500C.
Belastet Ring
Kan si du har et belastet ring og du trenger å vite feltet produsert fra det. Igjen vil vi ansette en av de mest viktige verktøy i fysikk, noe som gjør ting enklere. For det første vil vi bare se på felt langs aksen av ringen, ellers kan ting bare bli for komplisert, og det er ikke verdt innsatsen., Nå kan du bare ta en svært liten del av den ring og si at det er en sfære. Dette er egentlig ikke sant, men mindre vi gjøre delen jo mer vi kan gjøre det ligner et punkt kostnad. Så du har noe sånt som dette
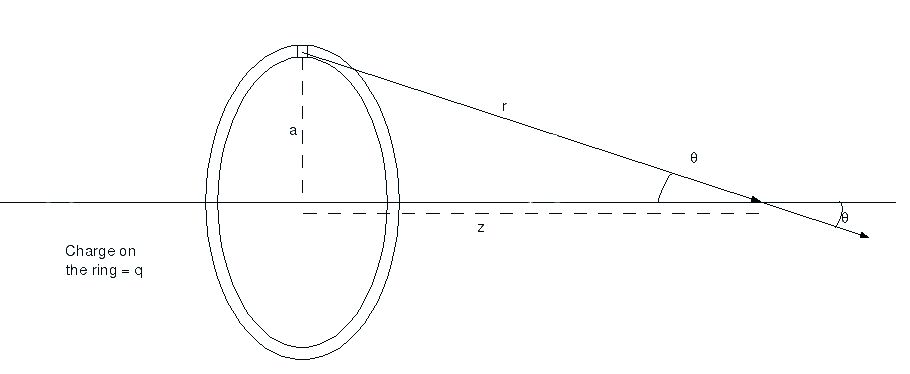
Du vil finne banen på et punkt 
langs aksen fra ringen av total kostnad og radius . Den lille firkanten øverst, det er den biten som du antar er et belastet område., Nå vet vi ikke hvor mye strøm det er i den lille delen som du kan gjøre det i hvilken som helst størrelse du ønsker, slik at vi bare ringe lade 
, en liten mengde av . Så vi har nå
hvis du Nå tenker på det, hver eneste bit av ringen over aksen presser ned vil ha en like stor bit nedenfor aksen skyve opp. Det vil også være den samme for venstre og høyre, og alle andre deler av ringen., Så all kraft fra ringen vil bare være opptrer langs den aksen. Å trene bare denne biten vi trenger å bruke noen av trigonometriske. Vi trenger til tider feltet av 
for å få den aksiale komponent.,
As you may or may not know can also be described (using SOH CAH TOA) by the following relationship for our situation
As is the adjacent side and is the hypotenuse., Så nå har vi
Men vi kan ikke vite hva som er. Vi vet radius av disken, , og den avstand vi er fra disk, .,er
Nå ønsker vi å bli kvitt som , så vi integrere
Nå vet vi fra figuren i starten av at den totale belastningen på disken , så hvis vi legger sammen alle de små bitene av den totale bør være , slik at integralet er bare .,
Så der har du det, – feltet fra et belastet disk. Alt du trenger er felt fra et punkt og noen trigonometriske kunnskap, og du kan arbeide det ut. Jeg kunne bare gitt deg den endelige løsningen, men denne måten kan du se hvor det kom fra, og så, hvis du glemmer det, kan du være i stand til å arbeide ut fra første prinsipper som ovenfor.,
Gauss’ Lov for Magnetisme
Dette er en fin og lett, men har noen store implikasjoner. Gauss’ Lov for Magnetisme er
Sine som vanlig gauss’ lov i at det beskriver et felt, denne gangen sine magnetiske felt, . Den sier at integralet av B over en lukket overflate, 
er null. Ingenting. Alle felt linje som går ut på overflaten har en tilsvarende som går i. Det er ingen samlet felt., Dette betyr at det er umulig å komme kilder til magnetfelt. Mens elektroner og protoner er opprinnelsen av feltet, og fra hvilket felt linjer avviker fra eller konvergere å, det er ingen magnetiske analog. Magnetiske feltlinjer er alltid lukkede sløyfer, ingen start og ingen ende. Dette kurset har ikke stoppet folk fra å forberede i tilfelle finner vi en magnetisk monopole.
Denne ligningen kan virke fint, og det er, men det er helt ubrukelig på sitt eget., Vanligvis et 0-resultat i fysikk er ganske viktig, det betyr at noe spesielt måtte skje, her viser magnetiske enpoler ikke eksisterer.
Faradays Lov
Nå er det stadig mer komplekse, her har vi Faradays lov,
jeg vil lede deg gjennom hver bit for å vise deg hva det egentlig betyr. Først har vi den venstre side som er lett. Dens bare som Gauss’ lov bare integralet over en annen ting., I stedet for å finne den totale – feltet gjennom en overflate, vi er nå å finne den totale – feltet rundt en lukket sløyfe 
. Det er alt som er annerledes med venstre side, ingen flere overflater, bare lukkede sløyfer. Nå på høyre side. Først opp, har vi et minus, og legg merke komplisert om det. Hvorfor det det vil bli forklart senere. Siden vi har en annen integrert, og dette ser forferdelig. 
symbol i utgangspunktet betyr en liten endring., Så 
er en endring i , og 
er en endring i 
, der er tid. Hele 
er endring av , dens hvor mye er i endring () i en gitt tid (). Og det er å bli integrert over et område ., er området inne i lukket sløyfe , hvis du tegner litt tilfeldig squiggly ting å sørge for at linjen ikke krysse seg selv, og at det knytter seg så lengden rundt linjen er din og området innenfor linjen er din . Enkle ja? Så totalt rundt en loop er akkurat lik minus skiftende gjennom løkken.
Hva skjer hvis det er ingen ?, Da er det vel ingen så er null, noe som gjør integralet 0, så ingen . Hva skjer hvis du har en konstant ? Godt igjen 0. Så er null, noe som gjør integralet 0, så igjen nei . Du kan bare indusere en – feltet fra et skiftende – feltet.,
viktigheten av minustegnet kommer fra det faktum at felt skape felt og felt skape felt (Som vist i Faraday ‘ s og Ampere Lover). Hvis minus var det ikke så feltene ville bare bygger og bygger til slutt gir uendelig energi, og det er ikke tillatt!
Ampère-Maxwell Loven
Den siste av Maxwell ‘ s Ligninger er Ampere-Maxwell loven., Akkurat som de to første lovene ble lignende så er de to siste, det er et mønster til dem i denne rekkefølgen, som kan gjøre dem lettere å huske. over et område, over et område, rundt en løkke, og nå endelig rundt en loop. Ligningen er
Venstre side, enkelt, integrert B rundt en lukket sløyfe. Høyre side, er ikke så lett., Første kan ignorere 
bit, jeg vil komme tilbake til det. Andre enn 
, sin svært lik Faradays lov. Har du en annen å endre feltet integrert over et område, men denne gangen sin . Denne gangen men i stedet for å multiplisere med minus 1 du multiplisere med 
. Igjen er dette to svært viktige verdier i fysikk, alene og kombinert. De er i hjertet av EM., Så din magnetiske feltet rundt en loop er akkurat lik endre E-feltet kan gå gjennom den tid av , men da må du legge på litt. Dette er den bit. Dette er bare den aktuelle går rundt løkken ganger av dette er fordi, som jeg sa i Ting i Bevegelse, hvis du har en bevegelse lade dvs. en strøm, så får du et magnetisk felt. Så du må legge til to biter sammen. Det gjøres.,
en Annen Form av den Dype Enden
Så vel som å skrive Maxwell ‘ s ligningene ovenfor, i det som kalles integrert form, du kan også skrive dem i differensial form som så
Enda en Form av den Dype Enden
Skrive Maxwell ‘ s ligninger i en av de to ovennevnte skjemaer er virkelig en forenkling., Både integrert form og differensial form er vektor ligninger og de spare deg for å måtte skrive ut hele 8 Maxwell ligninger for og felt i alle tre dimensjoner.,div id=»a2ea6619e6″> 
Well iot turns out you can also compactify the four vector Maxwell equations into two tensor equations like so
Here 
is a vector with four components, sometimes called the 4-current, and 
is a 4×4 matrix called the electromagnetic tensor., De er definert som
(6) 
(7) 
der 
er lysets hastighet. 
og 
bare fortelle deg hvor i vektor eller matrise til å se, men forvirrende for noen starter på 0, så 
og 
(må ikke forveksles med 
cubed). Samme med slik 
og 