Den vanlige icosahedron er ett av de fem Platonske faste stoffer. Det er en konveks vanlig polyhedron består av tjue trekantet ansikter, med fem møte i hver av de tolv knutepunktene. Det har 30 kanter og 12 noder. Sin dual polyhedron er dobbelt sekssidige.,
Mål
Hvis kanten lengden på en vanlig icosahedron er 
og radius av en lysende kule (tangent til hver av icosahedron ‘ s ansikter) er
mens midradius, som berører midten av hver kant, er
der 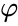

Areal og volum
areal 
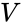

Kartesiske koordinater
følgende Kartesiske koordinater definere hjørnene i en icosahedron med kant-lengde 2, sentrert i origo:
der 
12 kantene på en vanlig oktahedron kan bli partisjonert i det gylne snitt, slik at den resulterende hjørnene definere en vanlig icosahedron. Dette gjøres ved først å plassere vektorene langs oktahedron er kantene slik at hvert ansikt er avgrenset av en syklus, da tilsvarende oppdeling hver kant inn i den gyldne middelvei langs retning av sin vektor., De fem octahedra å definere en gitt icosahedron danne en vanlig polyhedral forbindelsen, som gjør de to icosahedra som kan defineres på denne måten fra en gitt oktahedron.
Bygging av et system av equiangular linjer
følgende bygging av icoshaedron unngår kjedelige beregninger i feltet antall 
Eksistensen av icosahedron beløp til eksistensen av seks equiangular linjer i 
for å konstruere en slik equiangular systemet, starter vi med matrisen
av square størrelse 


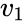
En enkel beregning gir 










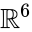



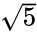

En annen grei bygging av icosahedron bruker representasjon teori av vekslende gruppe 
Stellations
Etter bestemte regler som er definert i boken fifty nine icosahedra, 59 stellations ble identifisert for den vanlige icosahedron. Den første formen er icosahedron seg selv., Den ene er en vanlig Kepler-knapt kunne skrive sitt morsmål solid. Tre er vanlig sammensatte polyedre.
| ansikter av icosahedron utvidet utover fly som skjærer hverandre, å definere områder i verdensrommet som vises av dette stellation diagram av kryss i ett plan., |
|||||
Geometric relations
| Icosahedron as a snub tetrahedron., |
Icosahedron as an alternated truncated octahedron. |
There are distortions of the icosahedron that, while no longer regular, are nevertheless vertex-uniform., Disse er invariant under samme rotasjoner som tetrahedrons, og er noe analogt til snub kube og snub dobbelt sekssidige, inkludert noen skjemaer som er chiral og noen med Th-symmetri, dvs. har forskjellige plan av symmetri fra tetrahedrons. Den icosahedron har et stort antall av stellations, inkludert en av Kepler-knapt kunne skrive sitt morsmål polyedre og noen av de faste forbindelser, som kan bli diskutert her.
icosahedron er unik blant Platonisk heldekkende objekter i besittelse av en dihedral vinkel ikke mindre enn 120°. Dens dihedral vinkel er ca 138.19°.,ss enn 120° og kan ikke brukes som ansikter av en konveks vanlig polyhedron fordi en slik konstruksjon ville ikke oppfyller kravet om at minst tre ansikter møte på et toppunkt og etterlate et positivt feil for folding i tre dimensjoner, icosahedra kan ikke brukes som celler i en konveks vanlig polychoron fordi, på samme måte, minst tre celler må møtes på en kant og etterlate et positivt feil for folding i fire dimensjoner (generelt for en konveks polytope i 
En icosahedron kan også bli kalt en gyroelongated pentagonal bipyramid., Det kan deles opp i en gyroelongated pentagonal pyramide og en femkantet pyramide eller i en femkantet antiprism og to like pentagonal pyramidene.
icosahedron kan også bli kalt en snub tetrahedrons, som snubification av en vanlig tetrahedrons gir en vanlig icosahedron., Alternativt, ved hjelp av nomenklaturen for snub polyedre som refererer til en snub kube som en snub cuboctahedron (cuboctahedron = rettes på kuben) og en snub dobbelt sekssidige som en snub icosidodecahedron (icosidodecahedron = utbedret dobbelt sekssidige), kan man ringe icosahedron den snub oktahedron (oktahedron = utbedret tetrahedrons).
En rettet icosahedron danner en icosidodecahedron.
Icosahedron vs dobbelt sekssidige
Når en icosahedron er innskrevet i en sfære, det opptar mindre av sfære volum (60.54%) enn en dobbelt sekssidige innskrevet i den samme sfære (66.49%).,
Også, så dette er soner, det er mulig å forvandle en til andre(Se nedenfor).,
| Icosahedron |
Truncated icosahedron |
Icosidodecahedron |
Truncated dodecahedron |
Dodecahedron |
Uses and natural forms
|
Electron micrograph av Herpes simplex virus. |
Mange virus, f.eks. herpes virus, har form av en icosahedron. Viral strukturer er bygget av gjentatt identiske protein underenhetene og icosahedron er den enkleste formen å montere ved hjelp av disse underenhetene. En vanlig polyhedron er brukt fordi det kan bygges fra en enkelt grunnleggende enhet protein som brukes igjen og igjen; dette sparer plass i viral genom., |
In 1904, Ernst Haeckel described a number of species of Radiolaria, including Circogonia icosahedra, whose skeleton is shaped like a regular icosahedron. A copy of Haeckel’s illustration for this radiolarian appears in the article on regular polyhedra.
|
Twenty-sided die., |
I noen rollespill spill, tjue-sided die (for kort, d20) er brukt for å bestemme suksess eller fiasko for en handling. Denne terningen er i form av en vanlig icosahedron. Det kan være nummerert fra «0» til «9» to ganger (i hvilken form det vanligvis fungerer som en ti-sided die, eller d10), men de fleste moderne versjoner er merket fra «1» til «20». Se d20-Systemet., |
En icosahedron er de tre-dimensjonale spill styret for Icosagame, tidligere kjent som Ico Crystal Spillet.
En icosahedron er brukt i den brettspill Scattergories for å velge en bokstav i alfabetet. Seks lite brukt bokstaver, for eksempel X, Q, Z, er utelatt.
Inne i en Magisk 8-Ball, ulike svar på ja / nei-spørsmål, skrives ut på en vanlig icosahedron.
icosahedron vises i en funksjonell form er sett i Sol de la Flor lys nyanse., Rosette dannet av to stykker vise en likhet til Frangipani blomster.
Hvis hver kant av en icosahedron er erstattet av en ohms motstand, motstand mellom motsatte hjørner er 0,5 ohm, og at mellom tilstøtende noder 11/30 ohm.
symmetri gruppe av icosahedron er isomorphic til vekslende gruppe på fem bokstaver. Dette nonabelian enkelt gruppe er det bare nontrivial normal undergruppe av den symmetriske gruppen på fem bokstaver., Siden Galois gruppe av de generelle quintic ligningen er isomorphic til den symmetriske gruppen på fem bokstaver, og det faktum at icosahedral gruppen er enkel og nonabelian betyr at quintic ligninger trenger ikke å ha en løsning i radikaler. Beviset av Abel-Ruffini teorem bruker dette enkle faktum, og Felix Klein skrev en bok som gjorde bruk av teorien om icosahedral symmetrier å utlede en analytisk løsning til den generelle quintic ligningen.,
Se også:
Mal:Wiktionarypar
- Avkortet icosahedron
- Vanlig polyhedron
- Geodesic nett bruke et iterativt bisected icosahedron for å generere nett på en sfære
- Jessen er icosahedron
Mal:Wikisource1911Enc
Mal:Commonscat
- Weisstein, Eric W., «Icosahedron» fra MathWorld.
- Papir modeller av icosahedron
- Uniform Polyedre
- K. J. M., MacLean, En Geometrisk Analyse av de Fem Platonske faste stoffer og Andre Semi-Regulære Polyedre
- Interaktiv Icosahedron modell – fungerer rett i nettleseren
- Virtual Reality Polyedre Encyclopedia of Polyedre
- Tulane.,edu er En diskusjon av super struktur og icosahedron
- Papir Modeller av Polyedre Mange lenker
- Origami Polyedre – Modellene er laget med en Modular Origami
- video av icosahedral speilet er en skulptur
Mal:Polyedre
az:Ikosaedrca:Icosàedrecs:Dvacetistěnda:Ikosaederet:Ikosaeedereo:Dudekedrofa:بیستوجهیit:Icosaedrohe:איקוסהדרוןlv:Ikosaedrshu:Ikozaédernl:Icosaëderno:Ikosaederpl:Dwudziestościan foremnypt:Icosaedrosimple:Icosahedronsq:Ikosaedri jeg rregulltsr:Икосаедарsv:Ikosaederta:brøt ut முக்கோணகம்th:ทรงยี่สิบหน้าuk:Ікосаедр.








