
Leonardo av Pisa (Fibonacci) (c.1170-1250)
Det 13. Århundre italienske Leonardo av Pisa, bedre kjent under kallenavnet Fibonacci, var kanskje den mest talentfulle Western matematiker i Middelalderen. Lite er kjent om hans liv, bortsett fra at han var sønn av en toll offisielle og, som et barn, han reiste rundt i Nord-Afrika-med sin far, der han lærte om arabisk matematikk., På hans retur til Italia, han hjalp til med å spre denne kunnskapen i hele Europa, og dermed setter i gang en foryngelse i Europeisk matematikk, som hadde ligget i stor grad i dvale i århundrer under den Mørke Middelalder.
I særdeleshet, i 1202, skrev han en svært innflytelsesrik bok som heter «Liber Abaci» («Book of Beregning»), der han fremmet bruken av Hindu-arabiske tallsystem, som beskriver dens mange fordeler for selgere og matematikere likt over klønete system av Romerske tall, deretter i bruk i Europa., Til tross for sine åpenbare fordeler, opptak av systemet i Europa var treg (dette var tross alt i løpet av tiden på Korstoget mot Islam, en tid som noe arabisk ble sett på med stor mistenksomhet), og arabisk tall ble utestengt i byen Firenze i 1299 på påskudd av at de var lettere å forfalske enn romertall. Men sunn fornuft til slutt seiret og det nye systemet ble innført i hele Europa av det 15. århundre, noe som gjør det Romerske systemet foreldet., Den horisontale linjen som notasjon for fraksjoner var også første gang brukt i dette arbeidet (selv om følgende arabisk praksisen med å plassere brøkdel til venstre for heltall).
Fibonacci-Sekvensen

oppdagelsen av de berømte Fibonacci-sekvensen
Fibonacci er best kjent, men hans introduksjon til Europa med et bestemt nummer-rekkefølge, som siden har blitt kjent som Fibonacci-Tall eller Fibonacci-Sekvensen., Han oppdaget rekkefølge – for det første rekursive rekke sekvens kjent i Europa – mens du vurderer et praktisk problem i «Liber Abaci» som involverer veksten av en hypotetisk befolkning på kaniner basert på idealiserte forutsetninger. Han bemerket at, etter hvert månedlige generasjon, antall par kaniner økt fra 1 til 2 til 3 til 5 og 8 til 13, etc, og peker på hvordan sekvensen kommet ved å legge de to foregående vilkår (i matematisk form, Fn = Fn-1 + Fn-2), en sekvens som kan i teorien utvide ubestemt tid.,
sekvensen, som faktisk hadde vært kjent for å Indiske matematikere siden det 6. Århundre, har mange interessante matematiske egenskaper, og mange av konsekvenser og relasjoner av sekvensen ble ikke oppdaget før flere hundre år etter Fibonacci ‘ s død., For eksempel sekvensen regenererer seg selv i noen overraskende måter: hver tredje F-tall er delelig med 2 (F3 = 2), hver fjerde F-tall er delelig med 3 (F4 = 3), hver femte F-tall er delelig med 5 (F5 = 5), hver sjette F-tall er delelig med 8 (F6 = 8), hver syvende F-tall er delelig med 13 (F7 = 13), osv., Tallene i sekvensen har også blitt funnet å være allestedsnærværende i naturen: blant andre ting, mange arter av blomstrende planter har antall kronblader i Fibonacci-Sekvensen; spiral arrangementer av ananas oppstå i 5s og 8s, de av kongler i 8-ere og 13s, og frøene av solsikke hoder i 21s, 34s, 55s eller enda høyere vilkårene i rekkefølge, etc.,
Golden Ratio φ
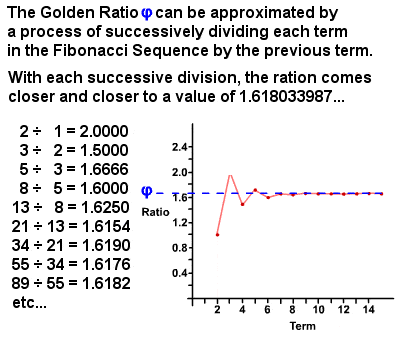
The Golden Ratio φ kan være avledet fra Fibonacci-Sekvensen
I 1750-årene, Robert Simson bemerket at forholdet av hver term i Fibonacci-Sekvensen til forrige termin nærmer seg, med stadig større nøyaktighet høyere vilkårene, et forhold på omtrent 1 : 1.6180339887 (det er faktisk en irrasjonell nummer lik (1 + √5)⁄2 som siden har blitt beregnet til tusenvis av desimaler)., Denne verdien er referert til som den Gylne snitt, også kjent som den Gyldne middelvei, Gylne snitt, Guddommelige Andel, osv., og er vanligvis merket med den greske bokstaven phi φ (eller noen ganger hovedstaden bokstaven Phi Φ). I hovedsak, to mengder er i det Gylne snitt dersom forholdet mellom summen av mengder til større mengde er lik forholdet mellom den større mengde til mindre en. Det Gylne snitt i seg selv har mange unike egenskaper, for eksempel 1⁄φ = φ – 1 (0.618…) og φ2 = φ + 1 (2.618…), og det finnes utallige eksempler på det å bli funnet både i naturen og i den menneskelige verden.,
Et rektangel med sider i forholdet 1 : φ er kjent som et gyllent Rektangel, og mange kunstnere og arkitekter gjennom historien (som kan dateres tilbake til det gamle Egypt og Hellas, men spesielt populært i Renessansens kunst av Leonardo da Vinci og hans samtidige) har proporsjonert deres fungerer omtrent bruk av det Gylne snitt og Gylne Rektangler, som er ansett for å være medfødt estetisk tiltalende. En arc-tilkobling motsatte punkter av stadig mindre nestede Gylne Rektangler former en logaritmisk spiral, kjent som en Gylne Spiral., Det Gylne snitt og Gylne Spiral kan også bli funnet i et overraskende antall forekomster i Naturen, fra skjell til blomster til dyrehorn for menneskelige organer til storm systemer for å fullføre galakser.,
Det bør bli husket, skjønt, at Fibonacci-Sekvensen var faktisk bare en svært liten element i «Liber Abaci» – ja, sekvensen bare mottatt Fibonacci navn i 1877 når Eduouard Lucas bestemte seg for å betale hyllest til ham ved å navngi serien etter ham – og som Fibonacci seg selv ikke var ansvarlig for å identifisere noen av de interessante matematiske egenskapene til sekvens, og dens forhold til den Gyldne middelvei og Gylne Rektangler og Spiraler, etc.,
Gitter Multiplikasjon
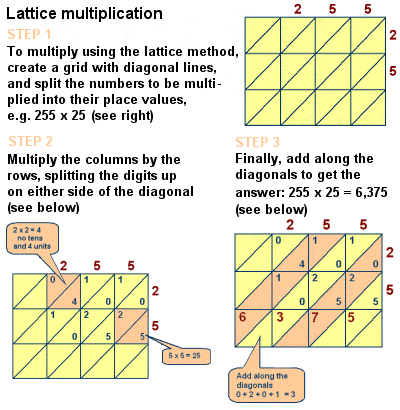
Fibonacci introdusert gitter multiplikasjon til Europa
Imidlertid bokens innflytelse på middelalderens matematikk er unektelig, og det gjør også omfatte diskusjoner om en rekke andre matematiske problemer, som for eksempel den Kinesiske restteoremet, perfekt tall og primtall, formler for aritmetiske serien og for plassen pyramidal tall, Euclidean geometriske bevis, og en studie av samtidige lineære ligninger langs linjene av Diophantus og Al-Karaji., Han beskrev også den gitter (eller sil) multiplikasjon metode for å multiplisere store tall, en metode som opprinnelig ble utviklet av Islamske matematikere som Al-Khwarizmi – algoritmer tilsvarende lang multiplikasjon.
Verken var «Liber Abaci» Fibonacci ‘ s eneste boken, selv om det var hans viktigste., Hans «Liber Quadratorum» («The Book of Squares»), for eksempel, er en bok om algebra, publisert i 1225 der vises en oppstilling av hva som nå kalles Fibonacci ‘ s identitet – noen ganger også kjent som Brahmagupta identitet etter mye tidligere Indiske matematiker som også kom til samme konklusjon – at produktet av to summer av to kvadrater er i seg selv en sum av to kvadrater f.eks. (12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,
| << Back to Medieval Mathematics | Forward to 16th Century Mathematics >> |