læringsutbytte
- Bli kjent med historien til stedsbestemt antall systemer
- Identifisere baser som har blitt brukt i antall systemer historisk
- Konvertere tall mellom baser
- Bruke to forskjellige metoder for konvertering av tall mellom baser
Bakgrunn
Som du kan forestille deg, er utviklingen av en base-systemet er et viktig skritt i å gjøre å telle prosessen mer effektiv., Vår egen base-ti-systemet oppsto trolig fra det faktum at vi har 10 fingre (inkludert tomlene) på to hender. Dette er en naturlig utvikling. Imidlertid, andre sivilisasjoner har hatt en rekke andre baser enn ti. For eksempel, de Innfødte i Queensland brukt en base-to-systemet, telle som følger: «en, to, to og to, ett, to, to, mye.»Noen Moderne Sør-American Stammene har en base-fem system telle på denne måten: «en, to, tre, fire, hånd, hånd og en hånd og to,» og så videre. Babylonerne brukte en base-seksti (sexigesimal) system., I dette kapitlet, vi pakker opp med et konkret eksempel på en sivilisasjon som faktisk brukt en base system enn 10.
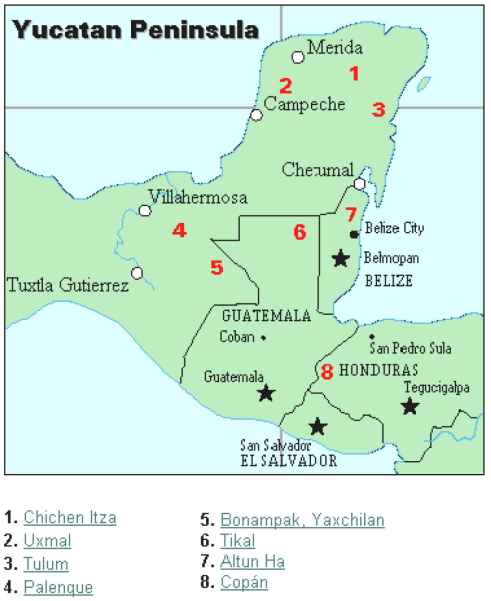Maya sivilisasjonen er generelt datert fra 1500 F.KR. til 1700 E.KR. Yucatan-Halvøya (se figur 16) i Mexico var åstedet for utvikling av en av de mest avanserte sivilisasjoner i den antikke verden. Mayaene hadde en sofistikert ritual system som var kontrollert av en preste-klasse. Denne klassen av prestene utviklet en filosofi med tid som guddommelig og evig., Kalenderen, og beregninger knyttet til det, var dermed svært viktig for den rituelle livet av preste-klassen, og dermed Maya-folket. Faktisk er mye av det vi vet om denne kulturen kommer fra kalenderen sin, poster og astronomi data. En annen viktig kilde til informasjon om Mayaene er skrevet av Far Diego de Landa, som gikk til Mexico som misjonær i 1549.
Det var to tall systemer utviklet av Mayaene—en for vanlige folk og en for prester., Ikke bare hadde disse to systemene bruker forskjellige symboler, de har også brukt ulike base-systemer. For prester, antall systemet ble styrt av ritualet. De dagene av året ble antatt å være guder, så det formelle symboler for de dager var innredet hoder, som utvalget til venstre Siden de grunnleggende kalenderen var basert på 360 dager, preste-tallsystem brukt en blandet base system ansette multispill på 20 og 360. Dette gir et forvirrende system, detaljer som vi vil hoppe over.,/td>
The Mayan Number System
Instead, we will focus on the numeration system of the «common” people, which used a more consistent base system., Som vi har nevnt tidligere, Mayaene brukte en base-20-system, kalt «vigesimal» system. Som systemet vårt, det er stedsbestemt, noe som betyr at plassering av en numerisk symbolet indikerer sin plass verdi. I tabellen nedenfor kan du se stedet verdi i sin vertikale format.
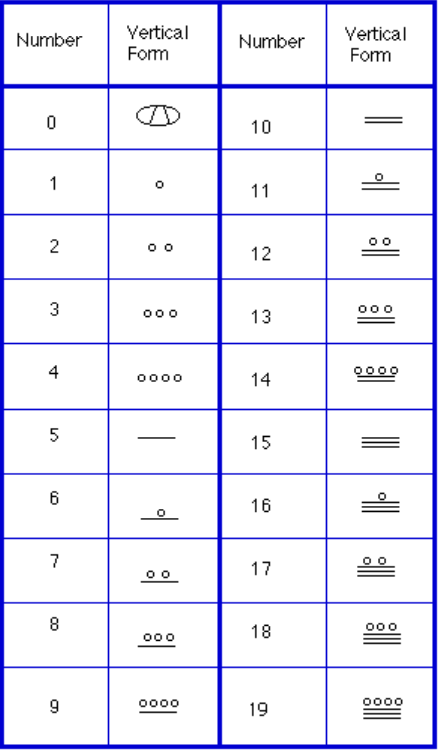
for å skrive tallene ned, var det bare tre symboler som trengs i dette systemet. En horisontal bar representerte antall 5, en prikk representert mengden 1, og et spesielt symbol (antatt å være en shell) representert null., Maya-system kan ha vært den første til å gjøre bruk av null som en plassholder/nummer. De første 20 tallene er vist i tabellen til høyre.
i Motsetning til vårt system, der de plasserer starter på høyre og går deretter til venstre, Maya-systemer steder de på bunnen av en vertikal retning og beveger seg opp som stedet verdi øker.
Når tallene er skrevet i vertikal form, så bør det aldri være mer enn fire prikker på et enkelt sted. Når du skriver Maya-tall, hver gruppe av fem prikker blir en bar., Også, det bør aldri være mer enn tre barer i et og samme sted…fire barer ville bli konvertert til en prikk i neste omgang opp. Det er det samme som 10 bli konvertert til en 1 i neste omgang opp når vi bærer i tillegg.
Eksempel
Hva er verdien av dette nummeret, som er vist på vertikal form?
Eksempel
Hva er verdien av følgende Maya-nummer?,
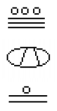
Prøv Det
Konverter Maya-nummer nedenfor til å basere 10.,
Eksempel
Konvertere base 10 antall 357510 til Maya-tall.
Skrive tall med baser større enn 10
Når bunnen av et tall er større enn 10, må du skille «siffer» med et komma for å gjøre separasjon av tallene klare.
For eksempel, i base-20, til å skrive tall som svarer til 17 × 202 + 6 × 201 + 13 × 200, vi vil skrive 17,6,1320.
I denne videoen presenterer vi flere eksempler på hvordan å skrive tall ved hjelp av Maya-tall, samt konvertere tall som er skrevet i Maya for i base 10 form.,
Den neste videoen viser flere eksempler på konvertering base 10 tall i Maya-tall.
Legge til Maya-Tall
Når du legger til Maya sammen tallene, vil vi innføre en ordning som Mayaene sannsynligvis ikke bruk, men som vil gjøre livet litt enklere for oss.
Eksempel
Legg til i Maya, tallene 37 29:
Prøv Det
Prøv å legge til 174 og 78 i Maya-ved først å konvertere til Maya-tall og så jobber utelukkende innenfor dette systemet. Ikke legg i base-ti (desimal) før helt på slutten når du kontrollere arbeidet.
I den siste videoen viser vi flere eksempler på å legge til Maya-tall.,
I denne modulen har vi kort skissert utvikling av tall og vår telling system, med vekt på «kort» del. Det er mange kilder til informasjon og forskning som fyller mange bind med bøker om dette emnet. Dessverre, vi kan ikke begynne å komme i nærheten av å dekke all den informasjonen som er der ute.
Vi har bare skrapet overflaten av det vell av forskning og informasjon som finnes på utvikling av tall og telling i hele menneskehetens historie., Hva er viktig å merke seg er at det systemet som vi bruker hver dag er et produkt av tusenvis av år med fremgang og utvikling. Det representerer bidrag av mange sivilisasjoner og kulturer. Det gjør ikke komme ned til oss fra himmelen, en gave fra gudene. Det er ikke etableringen av en lærebok utgiver. Det er faktisk så menneskelige som vi er, så er resten av matematikk. Bak hvert symbol, formel og regelen det er et menneskelig ansikt for å bli funnet, eller i det minste søkt.
Videre, vi håper at du nå har en grunnleggende forståelse for hvor interessant og variert antall systemer kan få., Også, vi er ganske sikker på at du også har begynt å erkjenne at vi tar våre egne tall system for gitt så mye som når vi prøver å tilpasse seg til andre systemer eller baser, befinner vi oss virkelig trenger å konsentrere seg og tenke på hva som skjer.