distributies
de kern van de problemen met de Dirac delta en soortgelijke wiskundige objecten is het probleem van Differentieerbaarheid. Zoals Dirac in het citaat hierboven zei, kom je niet echt in de problemen als je Zijn δ-functie gebruikt als een symbolische regel voor hoe het werkt op andere functies; hij gaat echter verder om δ te differentiëren in zijn berekeningen, en dit is waar de problemen echt beginnen., Hoe kan men a priori “wanneer deze handelingen zijn toegestaan” weten als men niet eens een vaste definitie van de objecten heeft, of wat het zou betekenen om ze te differentiëren? We zullen zien hoe deze vragen leiden tot de afleiding van nieuwe en rigoureus gedefinieerde wiskundige objecten.
Functionals
overweeg hoe men normaal de afgeleide (of primitieve) van een functie bepaalt. Onder normale omstandigheden, met” klassieke ” functies, heb je een goed gedefinieerde regel die beschrijft hoe een functie een verzameling van reële getallen afbeeldt naar een andere verzameling, zeg f : ℝ →ℝ., Gegeven dit en de definities van de integraal of afgeleide, kan men dan duidelijk de waarden onderzoeken die deze operators opleveren wanneer toegepast op de functie. In het geval van δ hebben we geen bruikbare definitie om in deze richting verder te gaan. In plaats daarvan wordt δ in de praktijk het duidelijkst gedefinieerd door de manier waarop het werkt op andere, goed gedefinieerde functies (zoals in (3)). Dit is het belangrijkste inzicht dat leidt tot de moderne verdelingstheorie. Het blijkt dat de juiste manier om δ en een grote klasse van soortgelijke objecten wiskundig te behandelen, is om te stoppen met proberen ze te definiëren als functies., Deze gedachtegang wordt goed beschreven door Jean Dieudonne in zijn overzicht van (zie ):
… men begint met een familie van zeer” regelmatige ” functies (meestal met
respect voor differentiële eigenschappen), die voldoen aan bepaalde (over het algemeen
integrale) relaties, of waarop bepaalde operaties mogelijk zijn; en
dan ontdekt men dat een a priori grotere familie van functies voldoet aan
dezelfde relaties, of kan worden onderworpen aan soortgelijke operaties. Veel
vragen kunnen dan natuurlijk worden gesteld: is deze nieuwe familie echt
anders dan de eerste?, Zo ja, wat zijn de relaties tussen de
twee families, en kan men een nauwkeurige beschrijving geven van de nieuwe?het is pas in de laatste fase van de “prehistorie” dat wat men een revolutionair standpunt zou kunnen noemen zal ontstaan, met het idee dat de “nieuwe familie” uit andere objecten dan functies zou kunnen bestaan.
de andere objecten waarnaar wordt verwezen zijn functionalen. U kunt een functionele
zien als een functie van functies., Aangezien een functie een unieke afbeelding is van de ene verzameling van
getallen naar de andere, kan een functionele F gedefinieerd worden als een afbeelding F: C →ℝ,
waarbij C een verzameling van functies is. Dat wil zeggen dat een functionele afbeelding functies toewijst aan reële
getallen., Een eenvoudig voorbeeld van een functionele van dit type is de bepaalde integraal:

die duidelijk duurt een functie f van een aantal van voldoende integreerbare functies en kaarten naar een reëel getal, de waarde van de integraal, of de oppervlakte onder de kromme van f(x) tussen a en b. Dit is slechts een enkel voorbeeld., Men kan zich een oneindig aantal functionalen en sets van functionalen voorstellen; men kan zelfs doorgaan met het veralgemenen en definiëren van toewijzingen van sets van functionalen naar reële getallen. Dat is hier noch daar. Belangrijk is dat het functionele concept gebruikt kan worden om distributies te definiëren.
de set testfuncties
we hebben nog een definitie nodig om ons doel te bereiken. Dit komt neer op het specificeren van de set C van functies van waaruit de distributies functies toewijzen aan reële getallen., Functies worden vaak verzameld in Verzamelingen die hun mate van continuïteit, Differentieerbaarheid en de continuïteit van hun derivaten specificeren. We zeggen dat een functie f in de verzameling C⁰ (schrijf f ∈ C⁰) is als deze continu is over de gehele reële Lijn in de zin dat de limiet op alle punten hetzelfde is wanneer genomen van links of rechts; het is niet noodzakelijk differentieerbaar. We zeggen dat f ∈ C1 als zijn afgeleide bestaat en continu is, dat wil zeggen f ‘ ∈ C⁰. Bijvoorbeeld, de functie g (x) = |x| is continu maar niet differentieerbaar bij x= 0; g is in C⁰ maar niet in C1., We kunnen dit generaliseren en zeggen dat Cⁿ de verzameling functies is die voor continue functies hun eerste n-derivaten hebben, waarbij n een geheel getal is.
naarmate n groter wordt, worden de Verzamelingen in zekere zin “kleiner”; je kunt altijd functies vinden (oneindig veel!) die in Cⁿ maar niet Cⁿ ⁺ 1. Deze” continuïteitsruimten ” vormen daarom een opeenvolging van geneste deelverzamelingen, zoals hieronder afgebeeld.

in de Buurt van de onderkant van deze oneindige reeks van sets van functies vinden we de set
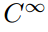
dat is natuurlijk de verzameling van alle functies die oneindig veel continue afgeleide. Veel bekende en vriendelijke functies bevinden zich in deze laatste klasse (bijvoorbeeld sin(x); cos(x); eˣ; alle veeltermen)., Deze functies worden “glad” of “goed gedragen” genoemd omdat men de werking van differentiatie op hen zo vaak kan uitvoeren als men wil zonder zorg. Maar hoewel deze set zeker oneindig veel leden heeft, zijn ze zeldzaam in de zin dat de meeste functies zich niet zo goed gedragen.
de verzameling die geschikt is voor de definitie van distributies is nog kleiner
dan deze. Het vereist een extra criterium: dat de functies compacte ondersteuning hebben. Deze technische term betekent simpelweg dat een functie niet-nulwaarden heeft binnen een eindig domein, en uniform nul is buiten dit domein., Daarom gebruiken we de notatie
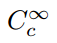
om de verzameling van oneindig continu differentieerbare functies met compacte ondersteuning aan te geven en deze functies testfuncties te noemen. Om een klasse functionalen te definiëren die deze set als domein gebruiken, moeten we er zeker van zijn dat er daadwerkelijk leden van deze set zijn., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

de definitie
vanaf dit punt is de definitie van een distributie eenvoudig. Een distributie is een lineair functioneel
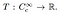
dat wil zeggen, het is een afbeelding van de set testfuncties naar een reëel getal. Analoog aan hoe een specifieke functie werkt op een inputnummer en een output produceert, worden specifieke distributies gedefinieerd door hoe ze testfuncties omzetten in getallen., De verdeling van de testfunctie φ kan worden geschreven als T (φ), Of algemeen als〈T, φ〉.
men kan nu zien waarom distributies gegeneraliseerde functies worden genoemd. Voor elke
klassieke functie waarvoor de integraal

is goed gedefinieerd, er is een overeenkomstige verdeling F zodanig dat 〈F,φ〉geeft de waarde van deze integraal is., Er zijn echter ook distributies die niet overeenkomen met klassieke functies; distributies zijn algemener. Zoals nu duidelijk zou moeten zijn, is het canonieke voorbeeld van een verdeling die niet overeenkomt met een klassieke functie de Dirac δ., Daarom zijn wij uiteindelijk terecht in een volledig strenge definitie van δ als de verdeling zodanig dat

De Gegeneraliseerde of “Zwak” Afgeleide
De δ distributie is slechts een van de oneindig vele distributies die niet
komen overeen met de klassieke functies. We kunnen er nog meer van verkrijgen door δ te differentiëren in de zin van verdelingen., Maar hoe lost het concept van een
distributie het probleem van differentiatie op, zoals eerder besproken? We hoeven alleen maar het concept van differentiatie te veralgemenen om van toepassing te zijn op distributies.
beschouw een functie f ∈ C1, zodat deze continu differentieerbaar is. Berekend aan de hand van integratie door delen, zien we dat

de term tussen haakjes verdwijnt omdat φ als testfunctie compacte ondersteuning heeft., Deze generalisatie ervan om een distributie, zeg F’, die overeenkomt met de functie f’:

Deze berekening de generalisatie ervan is vrij gemakkelijk om uitkeringen die niet overeenkomen met een klassieke functie f., Op deze manier kunnen we definiëren de afgeleide T’ van T in de zin van de uitkeringen:

Dit wordt soms ook aangeduid als de zwakke afgeleide, want het strekt zich uit van derivaten voor functies die normaal gesproken niet afleidbaar. Dit veralgemeniseert nog verder, naar hogere orde derivaten., We kunnen definiëren van de n-de afgeleide van een distributie T als T⁽ⁿ⁾, de laatste is waar de verdeling zodanig dat

Hier
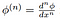
de klassieke afgeleide van de functie test, dat is zeker
om het bestaan door de definitie van de test functies!, Hieruit volgt dat alle distributies oneindig differentieerbaar zijn (in de zin van distributies).
Dit verwijdert volledig de strijd die Dirac en anderen ondervonden bij het differentiëren van de functie δ. Door wat we hier hebben gedefinieerd, een afgeleide van δ gewoon zeven voor de waarde van een andere functie afgeleide op nul., Formeel,

Dit biedt een rigoureus wiskundig kader voor de afgeleiden van δ die in de literatuur verschenen lang voordat deze theorie tot stand kwam.
Er zijn een aantal andere bewerkingen die van toepassing zijn op functies die zijn gegeneraliseerd om toe te passen op distributies. Zij kunnen worden toegevoegd en afgetrokken, geconvolueerd, en getransformeerd gebruikend Laplace en Fourier transformeert., Het is echter onmogelijk om de vermenigvuldiging van distributies te definiëren op een manier die de algebra behoudt die van toepassing is op klassieke functies (De Stelling van Schwartz-onmogelijkheid).