Introduction to Philosophy: Logic

Er is een oude visie, nog steeds wijdverspreid, dat wat de mens speciaal maakt – wat ons onderscheidt van de”beesten van het veld” —is dat we rationeel zijn. Waar bestaat rationaliteit uit? Dat is een netelige vraag, maar een mogelijke reactie gaat ruwweg als volgt: We manifesteren onze rationaliteit door activiteiten te ondernemen waarbij redeneren betrokken is—claims maken en ze ondersteunen met redenen, handelen in overeenstemming met redenen en overtuigingen, conclusies trekken uit beschikbaar bewijs, enzovoort.,

deze redeneeractiviteit kan goed en slecht worden gedaan; het kan correct of onjuist worden gedaan. Logica is de discipline die tot doel heeft om goed redeneren van slecht te onderscheiden.

goed redeneren is niet noodzakelijk effectief redeneren. In feite, zoals we zullen zien in een volgend hoofdstuk over logische drogredenen, is slecht redeneren alomtegenwoordig en vaak zeer effectief—in de zin dat mensen er vaak door worden overtuigd. In de logica is de standaard van goedheid niet effectiviteit in de zin van overtuigingskracht, maar juist volgens logische regels.,

denk bijvoorbeeld aan Hitler. Hij overtuigde een hele natie om mee te gaan met een verscheidenheid aan voorstellen die niet alleen vals maar ronduit slecht waren. Het zal je niet verbazen te horen dat als je het kritisch bekijkt, zijn redenering niet logisch is. Hitler ‘ s argumenten waren effectief, maar niet logisch correct. Bovendien gaan zijn overtuigende technieken verder dan redeneren in de zin van het ondersteunen van claims met redenen. Hitler vertrouwde op bedreigingen, emotionele manipulatie, niet-ondersteunde beweringen, enz. Er zijn veel retorische trucs die men kan gebruiken om te overtuigen.,

in logica bestuderen we de regels en technieken die ons in staat stellen om goed, correct redeneren te onderscheiden van slecht, onjuist redeneren.

omdat er een verscheidenheid van verschillende soorten redeneren en methoden zijn waarmee elk van deze typen te evalueren, plus verschillende uiteenlopende meningen over wat correct redeneren is, zijn er vele benaderingen van de logische onderneming. We praten over logica, maar ook over logica. Een logica is slechts een reeks regels en technieken om goed redeneren van slecht te onderscheiden., Een logica moet nauwkeurige normen formuleren voor de evaluatie van de redenering en methoden ontwikkelen voor de toepassing van die normen op specifieke gevallen.

basisbegrippen

redeneren omvat claims of verklaringen-ze maken en ondersteunen ze met redenen, het schetsen van de gevolgen ervan. Proposities zijn de dingen die we claimen, stellen, beweren.

proposities zijn het soort dingen dat waar of onwaar kan zijn. Ze worden uitgedrukt door declaratieve zinnen., We gebruiken zulke zinnen om allerlei beweringen te doen, van routinematige feiten (“de aarde draait om de zon”), tot grote metafysische stellingen (“de werkelijkheid is een onveranderlijk, karakterloos, Verenigd Absolute”), tot beweringen over moraliteit (“het is verkeerd om vlees te eten”).

Het is belangrijk om zinnen in de declaratieve stemming, die proposities uitdrukken, te onderscheiden van zinnen in andere stemmingen, die dat niet doen. Vragende zinnen stellen bijvoorbeeld vragen (“regent het?”), en imperatieve zinnen geven commando ‘ s (“don’ t drink kerosine.”)., Het heeft geen zin om te vragen of dit soort zinnen waarheden of onwaarheden uitdrukken, zodat ze geen proposities uitdrukken.

We onderscheiden ook proposities van de zinnen die ze uitdrukken, omdat een enkele propositie kan worden uitgedrukt door verschillende zinnen. “It’ s raining ” en “es regnet” drukken beide de stelling uit dat het regent; de ene zin doet het in het Engels, de andere in het Duits. Ook” John loves Mary “en” Mary is loved by John ” drukken beide dezelfde stelling uit.

de fundamentele redeneereenheid is het argument., In logica bedoelen we met “argument” niet een meningsverschil, een schreeuwmatch; eerder definiëren we de term precies:

Argument = een set van proposities, waarvan er één, de conclusie, wordt (verondersteld) ondersteund door de anderen, de premissen.

als we redeneren door claims te maken en ze te ondersteunen met redenen, dan is de claim die wordt ondersteund de conclusie van een argument; de redenen die worden gegeven om het te ondersteunen zijn de premissen van het argument., Als we redeneren door een gevolgtrekking te trekken uit een set verklaringen, dan is de gevolgtrekking die we trekken de conclusie van een argument, en de verklaringen waaruit het getrokken is zijn de premissen.

We nemen de hedge tussen haakjes—”verondersteld te zijn”—op in de definitie om ruimte te maken voor slechte argumenten. Een slecht argument, heel ruwweg, is er een waar de premissen niet de conclusie te ondersteunen; een goed argument de premissen daadwerkelijk ondersteunen de conclusie.

analyse van argumenten

de volgende passage drukt een argument uit:

dat geldt ook voor deze passage:

nogmaals, het uiteindelijke doel van logica is om argumenten te evalueren—om het goede van het slechte te onderscheiden. Om dit te doen vereist onderscheidingen, definities, principes en technieken die in de volgende hoofdstukken zullen worden geschetst. Voor nu zullen we ons richten op het identificeren en reconstrueren van argumenten.

de eerste taak is om argumenten uit te leggen—om expliciet hun premissen en conclusies te vermelden., Een duidelijke manier om dit te doen is simpelweg declaratieve zinnen op te sommen die de relevante stellingen uitdrukken, met een lijn die de premissen van de conclusie scheidt, dus: McDonald ‘ s betaalt hun werknemers zeer lage lonen.de dieren die McDonald ‘ s vlees leveren, worden onder erbarmelijke omstandigheden gekweekt.McDonald ‘ s voedsel is zeer ongezond.

Dit is een uitleg van de eerste argumentatieve passage hierboven., Om de conclusie van een argument te identificeren, is het nuttig om jezelf af te vragen: “Wat probeert deze persoon mij te overtuigen om te geloven door deze dingen te zeggen? Wat is het ultieme punt van deze passage?”Het antwoord is in dit geval vrij duidelijk. Een andere aanwijzing over wat er gaande is in de passage wordt gegeven door het woord “omdat” in de derde zin. Samen met andere woorden, zoals “Sinds” en “voor”, geeft het de aanwezigheid van een premisse aan. We kunnen zulke woorden premisse markers noemen. Het symbool “/ ∴ “kan daarom gelezen worden als afkorting voor”.,”Samen met uitdrukkingen als “bijgevolg,” “dus,” “volgt dat” en “wat impliceert dat,” “daarom” is een indicator dat de conclusie van het argument is op het punt om te volgen. We noemen dergelijke locutions conclusie markers. Een dergelijke marker is niet aanwezig in het eerste argument, maar we zien er wel een in het tweede, die als volgt kan worden uitgelegd:

1. het universum is enorm en complex.
2. het universum vertoont een verbazingwekkende graad van orde.
3. de planeten draaien rond de zon volgens reguliere wetten.
4. de kleinste delen van de dieren zijn precies afgestemd op hun doel.,
5. dergelijke volgorde en complexiteit kunnen niet willekeurig voorkomen.daarom moet het universum het product zijn van een ontwerper van enorme kracht en intellect: God.verschillende punten van vergelijking met onze eerste uitleg zijn hier het vermelden waard. Ten eerste, zoals gezegd, werden we gewaarschuwd voor de conclusie door het woord “daarom.”Ten tweede, deze passage vereist veel meer parafrase dan de eerste. De tweede zin is vragend, niet declaratief, en geeft dus geen stelling., Omdat argumenten per definitie collecties van stellingen zijn, moeten we ons beperken tot declaratieve zinnen wanneer we ze expliciteren. Aangezien het antwoord op de retorische vraag van de tweede zin duidelijk “ja” is, parafraseren we zoals getoond. De derde zin drukt twee stellingen uit, dus scheiden we ze in onze uitleg; elk daarvan is een premisse.

   dus soms, wanneer we een argument expliciteren, moeten we nemen wat er in de argumentatieve passage aanwezig is en het iets veranderen, zodat alle zinnen die we opschrijven de stellingen in het argument uitdrukken., Dit is parafraseren. Op andere momenten moeten we nog meer doen. We moeten bijvoorbeeld voorstellen invoeren die niet expliciet worden genoemd in de argumentatieve passage, maar die ongetwijfeld worden gebruikt in de redenering van het argument.

   Er is een Grieks woord voor argumentatieve passages die bepaalde stellingen onbesproken laten: enthymemes. Hier is een voorbeeld:

   er kan geen God zijn die alles liefheeft, omdat zoveel onschuldige mensen over de hele wereld lijden.,

   er schuilt hier een impliciete premisse op de achtergrond—iets dat nog niet is gezegd, maar dat waar moet zijn om het argument door te laten gaan. We hebben een claim nodig die het uitgangspunt verbindt met de conclusie—die de kloof tussen hen overbrugt. Zoiets als dit: een liefdevolle God zou niet toestaan dat onschuldige mensen lijden. Of misschien: wijdverbreid lijden is onverenigbaar met het idee van een alles liefhebbende godheid. De premisse wijst op lijden, terwijl de conclusie over God gaat; deze stellingen verbinden deze twee beweringen., Een volledige uitleg van de argumentatieve passage zou een stelling als deze expliciet maken:

   1. veel onschuldige mensen over de hele wereld lijden.een liefdevolle God zou niet toestaan dat onschuldige mensen lijden.
   2. / \daarom kan er geen God zijn die alles liefheeft.

   Dit is het kenmerk van de soorten stilzwijgende premissen die we willen blootleggen: als ze onwaar zijn, ondermijnen ze het argument., Vaak zijn dit soort zaken niet vermeld voor een reden: het zijn controversiële claims op hun eigen, die bewijs vereisen om ze te ondersteunen; dus de argumenteerder laat ze weg, liever niet vast komen te zitten. Maar als we ze eruit trekken, kunnen we een meer robuuste dialectische uitwisseling afdwingen, waarbij het argument op de kern van de zaak wordt gericht. In dit geval zou een discussie over de Verenigbaarheid van Gods goedheid en het kwaad in de wereld op zijn plaats zijn. Er valt veel te zeggen over dat onderwerp., Filosofen en theologen hebben door de eeuwen heen uitgebreide argumenten ontwikkeld om het idee te verdedigen dat Gods goedheid en menselijk lijden in feite verenigbaar zijn.

   tot nu toe is onze Analyse van argumenten niet bijzonder diepgaand geweest. We hebben opgemerkt dat het belangrijk is om de conclusie vast te stellen en duidelijk de premissen te vermelden, maar we hebben niet gekeken naar de manieren waarop sets van premissen hun conclusies kunnen ondersteunen. We hebben alleen maar vastgesteld dat de uitgangspunten gezamenlijk de conclusies ondersteunen., We hebben niet gekeken naar hoe ze dat doen, wat voor soort relaties ze met elkaar hebben. Dit vereist een diepere analyse.

   vaak ondersteunen verschillende premissen een conclusie—of een andere premisse—afzonderlijk, zonder hulp van anderen. Overweeg dit eenvoudige argument: de Amerikaanse invasie van Irak was een daad van agressie, geen zelfverdediging. Bovendien was het onredelijk te verwachten dat de voordelen van de oorlog opwegen tegen de onvermijdelijke verschrikkingen die deze zou ontketenen. Daarom, ③ de oorlog in Irak was niet een rechtvaardige oorlog.,

   stellingen 1 en 2 ondersteunen de conclusie, stelling 3-en ze doen dit onafhankelijk. Elk geeft ons een reden om te geloven dat de oorlog onrechtvaardig was, en elk staat als een reden, zelfs als we zouden veronderstellen dat de andere niet waar was; dit is het teken van onafhankelijke premissen.

   Het kan nuttig zijn, vooral wanneer argumenten complexer zijn, om diagrammen te tekenen die de relaties tussen premissen en conclusies weergeven., We zouden het bovenstaande argument als volgt kunnen weergeven:

   

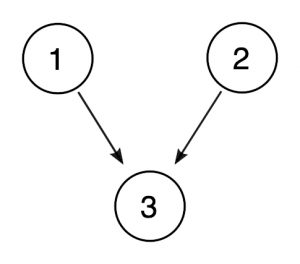
   In zo ‘ n diagram representeren de omcirkelde getallen de proposities en de pijlen de relatie van ondersteuning van de ene propositie naar de andere. Aangezien stellingen 1 en 2 elk 3 onafhankelijk ondersteunen, krijgen ze hun eigen pijlen.

   andere relaties tussen premissen zijn mogelijk. Soms bieden premissen slechts indirect ondersteuning voor conclusies, door ons een reden te geven om een andere premisse te geloven, die tussen de twee beweringen ligt., Overweeg het volgende argument:

   Po dichters zijn slechts “navolgers” wiens werken de waarheid verhullen; vandaar, ② zij hebben een corrumperende invloed op de zielen van burgers. Po dichters moeten daarom worden verbannen uit de ideale stadstaat.

   in dit voorbeeld biedt stelling 1 ondersteuning voor stelling 2 (het woord “vandaar” is een aanwijzing), terwijl stelling 2 direct de conclusie in 3 ondersteunt., We zouden de relaties tussen deze proposities als volgt weergeven:

   

   soms moeten premissen samenwerken om ondersteuning te bieden voor een andere claim, niet omdat een van hen reden geeft om de andere te geloven, maar omdat geen van beide op zichzelf de ondersteuning biedt die nodig is; we noemen dergelijke proposities gezamenlijke premissen. Overweeg het volgende:

   ① als echte kunstmatige intelligentie mogelijk is, dan moet men in staat zijn om een computer te programmeren om bewust te zijn. ② Maar het is onmogelijk om bewustzijn te programmeren. Daarom is echte kunstmatige intelligentie onmogelijk.,

   in dit argument ondersteunt noch premisse 1 noch premisse 2 de conclusie op zichzelf; integendeel, de tweede premisse verschaft als het ware een sleutel die de conclusie ontsluit uit de voorwaardelijke premisse 1. We kunnen een dergelijke onderlinge afhankelijkheid diagrammatisch met haakjes aangeven, dus:

   

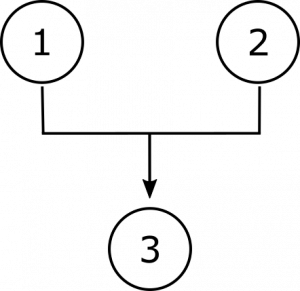
   diagrammen op deze manier kunnen nuttig zijn om te begrijpen hoe ze werken en om elke poging om kritisch met ze in contact te komen te informeren., In het eerste argument is duidelijk te zien dat eventuele overwegingen die in strijd zijn met een van de onafhankelijke vooronderstellingen, de steun voor de conclusie niet volledig zullen ondermijnen, omdat er nog een andere vooronderstelling is die haar een zekere mate van steun biedt. In het tweede argument zouden echter redenen die tegen het tweede uitgangspunt spreken, de steun voor de conclusie bij de wortel afsnijden; en alles wat in strijd is met het eerste uitgangspunt zal de tweede steun nodig hebben. En in het derde argument zullen overwegingen die in strijd zijn met een van de gemeenschappelijke uitgangspunten de steun voor de conclusie ondermijnen., Vooral wanneer argumenten complexer zijn, kunnen dergelijke visuele hulpmiddelen ons helpen alle gevolgtrekkingen in het argument te herkennen.

   misschien is het nuttig om af te sluiten met een iets complexer argument. Laten we eens kijken naar de aard van getallen:

   Numbers getallen zijn abstracte of concrete objecten. ② Het kunnen geen concrete objecten zijn, omdat ③ ze geen locatie in de ruimte hebben en ④ ze geen causale interactie hebben met andere objecten. Daarom zijn numbers getallen abstracte objecten.,

   de conclusie van dit argument is de laatste stelling, dat getallen abstracte objecten zijn. Merk op dat het eerste uitgangspunt ons een keuze geeft tussen deze bewering en een alternatief—dat ze concreet zijn. De tweede premisse ontkent dat alternatief, en dus werken premissen 1 en 2 samen om de conclusie te ondersteunen:

   

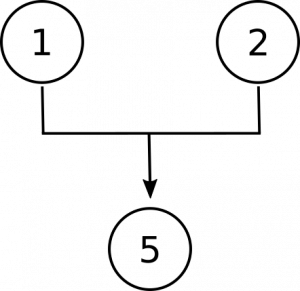
   nu moeten we ruimte maken in ons diagram voor stellingen 3 en 4. Ze zijn er om ons redenen te geven om te geloven dat getallen geen concrete objecten zijn., Ten eerste, door te beweren dat getallen zich niet in de ruimte bevinden zoals concrete objecten, en ten tweede door te beweren dat getallen niet interageren met andere objecten, zoals concrete objecten doen. Dit zijn aparte, onafhankelijke redenen om te geloven dat ze niet concreet zijn, dus we eindigen met dit diagram:

   

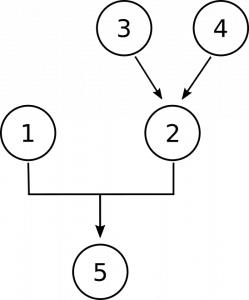
   logica en filosofie

   De kern van de logische onderneming is een filosofische vraag: wat maakt een goed argument? Dat wil zeggen, Wat is het voor een reeks claims om ondersteuning te bieden voor een andere claim? Of misschien: wanneer zijn we gerechtvaardigd in het trekken van gevolgtrekkingen?, Om deze vragen te beantwoorden, hebben logici een breed scala aan logische systemen ontwikkeld, die verschillende soorten argumenten omvatten en verschillende principes en technieken toepassen. Veel van de Hulpmiddelen die in de logica worden ontwikkeld, kunnen buiten de grenzen van de filosofie worden toegepast. De wiskundige die een stelling bewijst, de computerwetenschapper die een computer programmeert, de linguïst die de structuur van taal modelleert – al deze gebruiken logische methoden., Omdat logica zo ‘ n brede toepassing heeft, en vanwege de formele/wiskundige verfijning van vele logische systemen, neemt het een unieke plaats in in het filosofische curriculum. Een klasse in de logica is typisch in tegenstelling tot andere filosofie klassen in dat zeer weinig tijd wordt besteed direct bezig met en proberen om de “grote vragen” te beantwoorden; in plaats daarvan, komt men zeer snel neer op de business van het leren van logische formalismen. De vragen die logica probeert te beantwoorden zijn belangrijke filosofische vragen, maar de technieken die ontwikkeld zijn om ze te beantwoorden zijn het waard om ze zelf te bestuderen.,

   Dit betekent echter niet dat we logica en filosofie moeten beschouwen als louter tangentieel gerelateerd; integendeel, ze zijn diep met elkaar verweven. Voor alle formele toeters en bellen in de nieuwste high-end logische systeem, op de bodem is het onderdeel van een poging om de fundamentele vraag van wat volgt uit wat te beantwoorden. Bovendien is logica nuttig voor de praktiserende filosoof op ten minste drie andere manieren.filosofen proberen diepe, vervelende vragen te beantwoorden—over de aard van de werkelijkheid, wat een goed leven is, hoe een rechtvaardige samenleving te creëren, enzovoort., Ze geven hun antwoorden op deze vragen, en ze ondersteunen die antwoorden met redenen. Dan overwegen andere filosofen hun argumenten en antwoorden met uitwerkingen en kritieken-argumenten van hun eigen. Filosofie wordt gevoerd en maakt vooruitgang door middel van het uitwisselen van argumenten. Aangezien zij het primaire instrument van hun vak zijn, weten filosofen beter een beetje over wat goede argumenten oplevert! Logica is daarom essentieel voor de praktijk van de filosofie.,

   maar logica is niet alleen een hulpmiddel voor het evalueren van filosofische argumenten; Het heeft de loop van de lopende filosofische conversatie veranderd. Terwijl logici formele systemen ontwikkelden om de structuur van een steeds breder scala aan discursieve praktijken te modelleren, zijn filosofen in staat geweest om hun inzichten rechtstreeks toe te passen op traditionele filosofische problemen en eerder verborgen wegen van onderzoek te herkennen. Vooral sinds het begin van de 20e eeuw heeft de proliferatie van nieuwe benaderingen in de logica een revolutie in de praktijk van de filosofie teweeggebracht., Het is niet overdreven om te zeggen dat veel van de geschiedenis van de filosofie in de 20e eeuw een voortdurende poging vormde om te worstelen met nieuwe ontwikkelingen in de logica, en de filosofische focus op taal die ze leken te eisen. Geen enkel filosofisch onderwerp—van metafysica tot ethiek tot epistemologie en verder-werd onaangetast door deze revolutie.

   ten slotte is de logica zelf de bron van fascinerende filosofische vragen. De fundamentele vraag in zijn hart-Wat is het voor een claim te volgen van anderen?,- ramt uit in talloze richtingen, het verstrekken van vruchtbare grond voor filosofische speculatie. Er is logica, en dan is er de filosofie van de logica. Men zegt dat logica “formeel” is, bijvoorbeeld. Wat betekent dat? Het is een verrassend moeilijke vraag om te beantwoorden. Onze eenvoudigste logische formuleringen van voorwaardelijke zinnen (die met betrekking tot “als”), leiden tot schijnbare paradoxen. Hoe moeten die worden opgelost? Moeten onze formalismen worden aangepast om de natuurlijke taal betekenissen van conditionalen beter vast te leggen? Wat is eigenlijk de juiste relatie tussen logische systemen en natuurlijke talen?,

   traditioneel hebben de meeste logici geaccepteerd dat logica “bivalent” moet zijn: elke stelling is waar of onwaar. Maar natuurlijke talen bevatten vage termen waarvan de grenzen van toepasbaarheid niet altijd duidelijk zijn. Bijvoorbeeld “kaal”: voor bepaalde onderwerpen zouden we geneigd kunnen zijn om te zeggen dat ze goed op weg zijn naar volledige kaalheid, maar nog niet helemaal daar; aan de andere kant zouden we terughoudend zijn om te zeggen dat ze niet kaal zijn. Er zijn daartussen gevallen. Voor dergelijke gevallen zouden we bijvoorbeeld kunnen zeggen dat de stelling dat Fredo kaal is noch waar, noch onwaar is., Sommige logici hebben logica ‘ s ontwikkeld die niet bivalent zijn, om met dit soort taalverschijnsel om te gaan. Sommigen voegen een derde waarheidswaarde toe:” noch “of” onbepaald”, bijvoorbeeld. Anderen introduceren oneindige graden van waarheid (Dit wordt “fuzzy logic”genoemd). Deze logica ‘ s wijken af van traditionele benaderingen. Hebben ze dan in zekere zin ongelijk? Of hebben zij gelijk en de traditionalisten ongelijk? Of stellen we zelfs een verstandige vraag als we ons afvragen of een bepaald logisch systeem goed of fout is?, Kunnen we zogenaamde logische “pluralisten” zijn, die verschillende incompatibele logica ‘ s accepteren, afhankelijk van bijvoorbeeld of ze nuttig zijn?

   Dit soort vragen valt natuurlijk buiten het bestek van deze inleidende tekst. Ze zijn opgenomen om je een idee te geven van hoe ver je de studie van logica kan nemen. De taak voor nu is echter om met die studie te beginnen.

   leg eerst de volgende argumenten uit, parafraserend waar nodig en alleen met inbegrip van stilzwijgende premissen wanneer dit uitdrukkelijk is geïnstrueerd. Vervolgens, diagram de argumenten.,

   1. getallen, als ze al bestaan, moeten concrete of abstracte objecten zijn. Concrete objecten – zoals planeten en mensen–zijn in staat om te interageren met andere dingen in oorzaak-en-gevolg relaties. Getallen missen dit vermogen. Daarom zijn getallen abstracte objecten. afschaffing van de doodstraf! Waarom? Het is immoreel. Talrijke studies hebben aangetoond dat er raciale vooringenomenheid in de toepassing ervan. De opkomst van DNA-testen heeft tientallen gevangenen in de dodencel vrijgesproken; wie weet hoeveel onschuldige mensen er in het verleden zijn gedood? De doodstraf is ook onpraktisch., Wraak is contraproductief:” oog om oog maakt de hele wereld blind”, zoals Gandhi zei. Bovendien zijn de kosten van het proces tegen de doodstraf, met hun eindeloze beroepsmogelijkheden, enorm.
   2. een rechtvaardig economisch systeem zou een billijke verdeling van de hulpbronnen en een afwezigheid van exploitatie kennen. Het kapitalisme is een onrechtvaardig economisch systeem. Onder het kapitalisme is de typische verdeling van rijkdom zeer scheef ten gunste van de rijken., En werknemers worden uitgebuit: ondanks hun essentiële rol bij de productie van goederen voor de markt, gaat het grootste deel van de winst uit de verkoop van die goederen naar de eigenaars van bedrijven, niet naar hun werknemers.de geest en de hersenen zijn niet identiek. Hoe kunnen dingen identiek zijn als ze verschillende eigenschappen hebben? Er is een eigenschap die de geest en de hersenen niet delen: de hersenen zijn deelbaar, maar de geest niet. Zoals alle materiële dingen, kunnen de hersenen worden verdeeld in delen—verschillende helften, regio ‘ s, neuronen, enz. Maar de geest is een eenheid. Het is mijn denkende essentie, waarin ik geen afzonderlijke delen kan onderscheiden., elke gezonde volwassene moet aan de beroepsbevolking deelnemen. Hoe meer mensen werken, hoe groter de rijkdom van de natie, wat iedereen economisch ten goede komt. Bovendien is er geen vervanging voor de waardigheid werknemers vinden op het werk. De overheid zou daarom belastingkredieten moeten verstrekken om mensen aan te moedigen aan de slag te gaan.
   1. de symbolen voorafgaand aan de conclusie, “/ \daarom” vertegenwoordigen het woord “daarom.”↵
   2. Dit is niet altijd de reden., Sommige claims worden stilzwijgend gelaten, simpelweg omdat iedereen ze accepteert en om ze expliciet te vermelden zou een verspilling van tijd zijn. Als we beweren: “olifanten zijn zoogdieren, en zo warmbloedig,” laten we de bewering achterwege dat alle zoogdieren warmbloedig zijn om deze onschuldige reden. ↵
   3. deze argumenten hebben zelfs een speciale naam: ze worden “theodicies” genoemd.”↵
   4. een extreem gecomprimeerde versie van Plato ‘ s bezwaren tegen poëzie in boek X van de Republiek. ↵
   5. John MacFarlane besteedt in zijn veelgelezen proefschrift meer dan 300 pagina ‘ s aan die vraag. Zie: MacFarlane, J. 2000., “Wat betekent het om te zeggen dat Logica formeel Is?”University Of Pittsburgh. ↵
   6. voor een beknopte uitleg, zie de Wikipedia entry on paradoxes of material implicatie. ↵
   7. een vereenvoudigde versie van een argument van Rene Descartes. ↵

   de ondubbelzinnige betekenis van declaratieve zinnen.

   zinnen die aangeven dat iets al dan niet het geval is. Bijvoorbeeld, ” Bob won de 50m freestyle.,”Declaratieve zinnen kunnen worden vergeleken met degenen die vragen stellen, genaamd vragende zinnen, en degenen die commando’ s leveren, bekend als imperatieve zinnen. (Declaratieve zinnen zijn ook bekend als indicatieve zinnen)

   woorden die in het algemeen aangeven wat volgt is een premisse, bijvoorbeeld “given that,” “as,” “since.”

   woorden die in het algemeen aangeven dat wat volgt een conclusie is, bijvoorbeeld “daarom,” “dus,” “bijgevolg.”

   argumenten die bepaalde premissen onbesproken laten.,

   premissen die tot doel hebben op zichzelf voldoende ondersteuning te bieden voor de waarheid van de conclusie.

   premissen die niet de conclusie van een argument, maar een andere premisse rechtstreeks ondersteunen.

   premissen die alleen ondersteuning bieden voor de waarheid van de conclusie in combinatie.