LEONARDO Fibonacci – Italiaanse wiskundige (schreef LEBER ABACI)

Leonardo van Pisa (Fibonacci) (CA.1170-1250)

de 13de eeuwse Italiaan Leonardo van Pisa, beter bekend onder zijn bijnaam Fibonacci, was misschien wel de meest getalenteerde westerse wiskundige van de Middeleeuwen. Er is weinig bekend over zijn leven, behalve dat hij de zoon was van een douaneambtenaar en als kind reisde hij door Noord-Afrika met zijn vader, waar hij leerde over Arabische wiskunde., Bij zijn terugkeer naar Italië hielp hij deze kennis in heel Europa te verspreiden, waardoor hij een verjonging in de Europese wiskunde op gang bracht, die gedurende eeuwen in de Middeleeuwen grotendeels inactief was geweest.in het bijzonder schreef hij in 1202 een enorm invloedrijk boek genaamd “Liber Abaci” (“Boek van berekening”), waarin hij het gebruik van het Hindoe-Arabisch cijfersysteem promootte, waarin hij de vele voordelen beschreef voor zowel handelaren als wiskundigen ten opzichte van het onhandige systeem van Romeinse cijfers dat toen in Europa werd gebruikt., Ondanks de voor de hand liggende voordelen was de invoering van het systeem in Europa traag (dit was immers tijdens de kruistochten tegen de Islam, een tijd waarin alles wat Arabisch was met grote argwaan bekeken), en Arabische cijfers werden zelfs verboden in de stad Florence in 1299 Onder het voorwendsel dat ze gemakkelijker te vervalsen waren dan Romeinse cijfers. Echter, gezond verstand uiteindelijk zegevierde en het nieuwe systeem werd aangenomen in heel Europa door de 15e eeuw, waardoor het Romeinse systeem verouderd., De horizontale balk notatie voor breuken werd ook voor het eerst gebruikt in dit werk (hoewel volgens de Arabische praktijk van het plaatsen van de breuk links van het gehele getal).

Fibonacci-sequentie

De ontdekking van de beroemde Fibonacci-sequentie

Fibonacci is echter het meest bekend vanwege zijn introductie in Europa van een bepaalde getallenreeks, die sindsdien bekend is geworden als Fibonacci-getallen of de Fibonacci-sequentie., Hij ontdekte de sequentie – de eerste recursieve getallenreeks die in Europa bekend is-terwijl hij een praktisch probleem in de “Liber Abaci” overwoog waarbij de groei van een hypothetische populatie konijnen gebaseerd was op geïdealiseerde veronderstellingen. Hij merkte op dat, na elke maandelijkse generatie, het aantal paren van konijnen steeg van 1 naar 2 naar 3 naar 5 naar 8 naar 13, enz., en identificeerde hoe de opeenvolging vorderde door de vorige twee termen (in wiskundige termen, Fn = Fn-1 + Fn-2) toe te voegen, een opeenvolging die in theorie onbeperkt kon duren.,

de sequentie, die eigenlijk al bekend was bij Indiase wiskundigen sinds de 6e eeuw, heeft veel interessante wiskundige eigenschappen, en veel van de implicaties en relaties van de sequentie werden pas enkele eeuwen na de dood van Fibonacci ontdekt., Zo regenereert de reeks zichzelf op een aantal verrassende manieren: elk derde F-getal is deelbaar door 2( F3 = 2), elk vierde F-getal is deelbaar door 3 (F4 = 3), elk vijfde F-getal is deelbaar door 5 (F5 = 5), elk zesde F-getal is deelbaar door 8 (F6 = 8), elk zevende F-getal is deelbaar door 13 (F7 = 13), enz., De nummers van de reeks is ook gevonden alomtegenwoordig in de natuur: onder andere, veel soorten bloeiende planten hebben nummers van bloemblaadjes in de Fibonacci-reeks; De spiraalvormige regelingen van ananassen komen voor in 5s en 8s, die van dennenappels in 8s en 13s, en de zaden van zonnebloem hoofden in 21s, 34s, 55s of zelfs hogere termen in de reeks; enz.,de gulden snede φ

de gulden snede φ

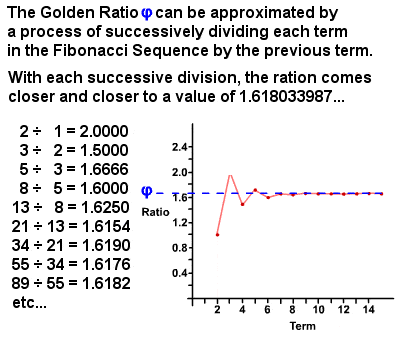
De Gulden Snede φ kan worden afgeleid uit de Fibonacci-sequentie

in de jaren 1750 merkte Robert Simson op dat de verhouding van elke term in de Fibonacci-sequentie tot de vorige termbenaderingen, met steeds grotere nauwkeurigheid, een verhouding van ongeveer 1 : 1,6180339887 (het is eigenlijk een irrationeel getal gelijk aan (1 + √5) 2 2 dat sindsdien is berekend op duizenden decimalen)., Deze waarde wordt aangeduid als de gulden snede, ook bekend als de gulden snede, Gulden Snede, goddelijke Verhouding, etc, en wordt meestal aangeduid met de Griekse letter phi φ (Of soms de hoofdletter Phi Φ). In wezen zijn twee hoeveelheden in de gulden snede als de verhouding van de som van de hoeveelheden tot de grotere hoeveelheid gelijk is aan de verhouding van de grotere hoeveelheid tot de kleinere. De gulden snede zelf heeft vele unieke eigenschappen, zoals 1 φ φ = φ-1 (0,618…) en φ2 = φ + 1 (2,618…), en er zijn talloze voorbeelden van te vinden, zowel in de natuur als in de menselijke wereld.,een rechthoek met zijden in de verhouding 1 : φ staat bekend als een gouden rechthoek, en vele kunstenaars en architecten door de geschiedenis heen (daterend uit het oude Egypte en Griekenland, maar vooral populair in de Renaissance kunst van Leonardo Da Vinci en zijn tijdgenoten) hebben hun werken ongeveer geproportioneerd met behulp van de Gulden Ratio en gouden rechthoeken, die algemeen worden beschouwd als aangeboren esthetisch aantrekkelijk. Een boog die tegengestelde punten verbindt van steeds kleinere geneste gouden rechthoeken vormt een logaritmische spiraal, bekend als een gouden spiraal., De gulden snede en gouden spiraal kan ook worden gevonden in een verrassend aantal gevallen in de natuur, van schelpen tot bloemen tot dierlijke hoorns tot menselijke lichamen tot stormsystemen tot complete melkwegstelsels.,men moet echter niet vergeten dat de Fibonacci – sequentie eigenlijk slechts een heel klein element was in “Liber Abaci” – de sequentie kreeg pas de naam van Fibonacci in 1877 toen Eduouard Lucas besloot hem eer te bewijzen door de reeks naar hem te vernoemen-en dat Fibonacci zelf niet verantwoordelijk was voor het identificeren van de interessante wiskundige eigenschappen van de sequentie, de relatie met de gulden middenweg en gouden rechthoeken en spiralen, enz.,

Rooster Vermenigvuldiging

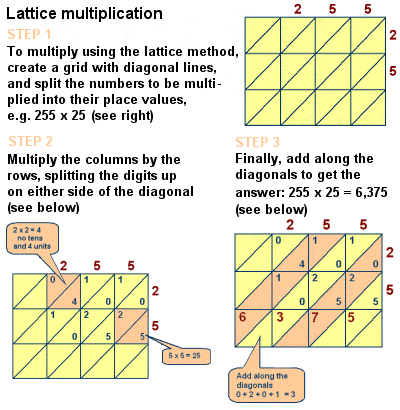
Fibonacci geïntroduceerd rooster vermenigvuldiging in Europa

Echter, het boek is van invloed op de middeleeuwse wiskunde is niet te ontkennen, en het is ook de bespreking van een aantal andere wiskundige problemen, zoals de Chinese Rest Stelling, perfecte getallen en priemgetallen, formules voor rekenkundige reeks en voor vierkante piramidale nummers, de Euclidische geometrische bewijzen, en een studie van simultane vergelijkingen langs de lijnen van Diophantus en Al-Karaji., Hij beschreef ook de lattice (of zeef) vermenigvuldigingsmethode voor het vermenigvuldigen van grote getallen, een methode-oorspronkelijk ontwikkeld door Islamitische wiskundigen zoals al – Khwarizmi-algoritmisch equivalent aan lange vermenigvuldiging.

evenmin was “Liber Abaci” Fibonacci ‘ s enige boek, hoewel het zijn belangrijkste boek was., Zijn “Liber Quadratorum” (“het Boek der vierkanten”), bijvoorbeeld, is een boek over de algebra, gepubliceerd in 1225 waarin een verklaring verschijnt van wat nu Fibonacci ’s identiteit wordt genoemd – soms ook bekend als Brahmagupta’ s identiteit naar de veel eerdere Indiase wiskundige die ook tot dezelfde conclusies kwam – dat het product van twee sommen van twee vierkanten zelf een som van twee vierkanten is.(12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,