leerresultaten
- vertrouwd raken met de geschiedenis van positionele getallensystemen
- Identificeer bases die historisch gebruikt zijn in getallensystemen
- converteer getallen tussen bases
- gebruik twee verschillende methoden voor het converteren van getallen tussen bases
Achtergrond
zoals u zich kunt voorstellen, is de ontwikkeling van een basissysteem een belangrijke stap om het telproces efficiënter te maken., Ons eigen base-ten systeem is waarschijnlijk ontstaan uit het feit dat we 10 vingers (inclusief duimen) op twee handen hebben. Dit is een natuurlijke ontwikkeling. Andere beschavingen hebben echter een verscheidenheid aan andere bases dan tien. De inwoners van Queensland gebruikten bijvoorbeeld een base-two-systeem, dat als volgt telde: “one, two, two and one, two two’ s, much.”Sommige moderne Zuid-Amerikaanse stammen hebben een basis-vijf systeem dat op deze manier telt: “een, twee, drie, vier, hand, hand en een, hand en twee,” enzovoort. De Babyloniërs gebruikten een basis-zestig (sexigesimaal) systeem., In dit hoofdstuk sluiten we af met een specifiek voorbeeld van een beschaving die een ander basissysteem dan 10 gebruikte.
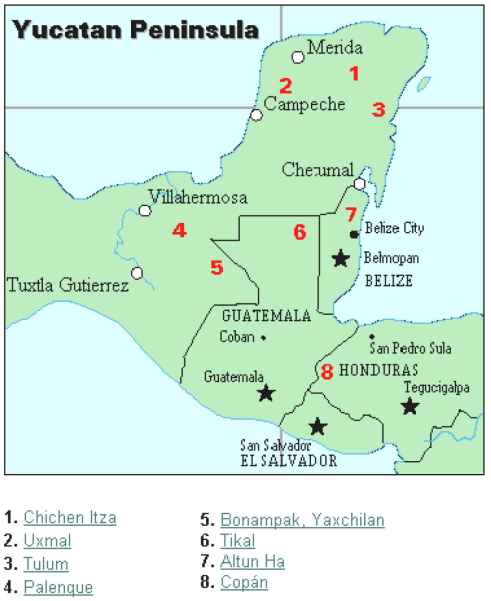 de Maya beschaving is over het algemeen gedateerd van 1500 v.Chr. tot 1700 n. Chr. Het schiereiland Yucatan (zie Figuur 16) in Mexico was het toneel voor de ontwikkeling van een van de meest geavanceerde beschavingen van de oude wereld. De Maya ‘ s hadden een verfijnd ritueel systeem dat onder toezicht stond van een priesterlijke klasse. Deze klasse van priesters ontwikkelde een filosofie met de tijd als goddelijk en eeuwig., De kalender, en de bijbehorende berekeningen, waren dus zeer belangrijk voor het rituele leven van de priesterlijke klasse, en dus het Maya-volk. In feite komt veel van wat we weten over deze cultuur uit hun kalenderregisters en astronomische gegevens. Een andere belangrijke bron van informatie over de Maya ‘ s zijn de geschriften van Pater Diego de Landa, die in 1549 als missionaris naar Mexico ging.
de Maya beschaving is over het algemeen gedateerd van 1500 v.Chr. tot 1700 n. Chr. Het schiereiland Yucatan (zie Figuur 16) in Mexico was het toneel voor de ontwikkeling van een van de meest geavanceerde beschavingen van de oude wereld. De Maya ‘ s hadden een verfijnd ritueel systeem dat onder toezicht stond van een priesterlijke klasse. Deze klasse van priesters ontwikkelde een filosofie met de tijd als goddelijk en eeuwig., De kalender, en de bijbehorende berekeningen, waren dus zeer belangrijk voor het rituele leven van de priesterlijke klasse, en dus het Maya-volk. In feite komt veel van wat we weten over deze cultuur uit hun kalenderregisters en astronomische gegevens. Een andere belangrijke bron van informatie over de Maya ‘ s zijn de geschriften van Pater Diego de Landa, die in 1549 als missionaris naar Mexico ging.
 er waren twee telersystemen ontwikkeld door de Maya ‘ s—één voor het gewone volk en één voor de priesters., Niet alleen gebruikten deze twee systemen verschillende symbolen, ze gebruikten ook verschillende basissystemen. Voor de priesters werd het getalsysteem beheerst door rituelen. De dagen van het jaar werden beschouwd als goden, dus de formele symbolen voor de dagen werden versierd hoofden, zoals de steekproef aan de linkerkant aangezien de basiskalender was gebaseerd op 360 dagen, het priesterlijk cijfer systeem gebruikt een gemengd basissysteem gebruikmakend veelvouden van 20 en 360. Dit zorgt voor een verwarrend systeem, waarvan we de details zullen overslaan.,/td>
er waren twee telersystemen ontwikkeld door de Maya ‘ s—één voor het gewone volk en één voor de priesters., Niet alleen gebruikten deze twee systemen verschillende symbolen, ze gebruikten ook verschillende basissystemen. Voor de priesters werd het getalsysteem beheerst door rituelen. De dagen van het jaar werden beschouwd als goden, dus de formele symbolen voor de dagen werden versierd hoofden, zoals de steekproef aan de linkerkant aangezien de basiskalender was gebaseerd op 360 dagen, het priesterlijk cijfer systeem gebruikt een gemengd basissysteem gebruikmakend veelvouden van 20 en 360. Dit zorgt voor een verwarrend systeem, waarvan we de details zullen overslaan.,/td>
The Mayan Number System
Instead, we will focus on the numeration system of the “common” people, which used a more consistent base system., Zoals we al eerder zeiden, gebruikten de Maya ‘ s een base-20 systeem, het zogenaamde “vigesimal” systeem. Net als ons systeem is het positioneel, wat betekent dat de positie van een numeriek symbool de plaatswaarde aangeeft. In de volgende tabel kunt u de plaatswaarde in het verticale formaat zien.
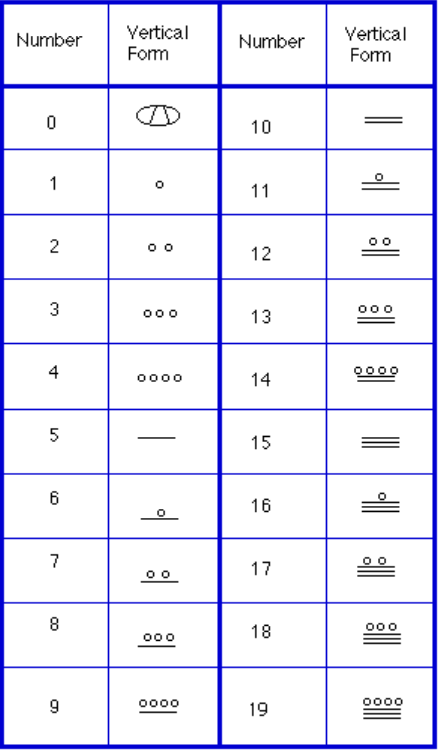
om getallen neer te schrijven waren er slechts drie symbolen nodig in dit systeem. Een horizontale balk vertegenwoordigde de hoeveelheid 5, een punt vertegenwoordigde de hoeveelheid 1, en een speciaal symbool (vermoedelijk een shell) vertegenwoordigde nul., Het Maya-systeem kan de eerste zijn geweest die gebruik maakte van nul als plaatshouder/nummer. De eerste 20 nummers staan in de tabel rechts.
In tegenstelling tot ons systeem, waar de enen aan de rechterkant beginnen en dan naar links gaan, plaatsen de Maya-systemen de enen aan de onderkant van een verticale oriëntatie en gaan omhoog als de plaatswaarde toeneemt.
wanneer getallen in verticale vorm worden geschreven, mogen er nooit meer dan vier punten op één plaats zijn. Bij het schrijven van Maya-nummers wordt elke groep van vijf punten één maat., Ook, er mag nooit meer dan drie bars op een enkele plaats…vier bars zou worden omgezet in een punt in de volgende plaats omhoog. Het is hetzelfde als 10 worden omgezet naar een 1 in de volgende plaats omhoog wanneer we dragen tijdens de optelling.
voorbeeld
Wat is de waarde van dit getal, dat in verticale vorm wordt weergegeven?
voorbeeld
Wat is de waarde van het volgende Maya-getal?,
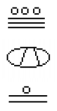
probeer het
converteer het onderstaande Maya-Nummer Naar basis 10.,

voorbeeld
converteer het basis 10-nummer 357510 naar Maya cijfers.
schrijf getallen met basen groter dan 10
wanneer de basis van een getal groter is dan 10, scheid elk “cijfer” met een komma om de scheiding van cijfers duidelijk te maken.
bijvoorbeeld, in BASIS 20, om het getal te schrijven dat overeenkomt met 17 × 202 + 6 × 201 + 13 × 200, we zouden 17,6,1320 schrijven.
In de volgende video geven we meer voorbeelden van het schrijven van getallen met Maya-cijfers en het converteren van cijfers geschreven in Maya voor in basis 10 vorm.,
de volgende video toont meer voorbeelden van het omzetten van basis 10 getallen in Maya cijfers.
het toevoegen van Maya-nummers
wanneer we Maya-nummers bij elkaar optellen, nemen we een schema aan dat de Maya ‘ s waarschijnlijk niet gebruikten, maar dat het leven voor ons een beetje makkelijker zal maken.
voorbeeld
voeg in Mayan de Nummers 37 en 29 toe:

probeer het
probeer 174 en 78 in Mayan toe te voegen door eerst naar Maya-nummers te converteren en dan volledig binnen dat systeem te werken. Niet toevoegen in base-ten (decimaal) tot het einde wanneer u uw werk te controleren.
In de laatste video laten we meer voorbeelden zien van het toevoegen van Maya-cijfers.,
in deze module hebben we kort de ontwikkeling van getallen en ons telsysteem geschetst, met de nadruk op het “korte” gedeelte. Er zijn tal van bronnen van informatie en onderzoek die vele volumes van boeken over dit onderwerp te vullen. Helaas kunnen we niet in de buurt komen van alle informatie die er is.

we hebben slechts de oppervlakte van de rijkdom aan onderzoek en informatie die bestaat over de ontwikkeling van getallen en tellen door de menselijke geschiedenis heen bekrast., Wat belangrijk is om op te merken is dat het systeem dat we elke dag gebruiken is een product van duizenden jaren van vooruitgang en ontwikkeling. Het vertegenwoordigt bijdragen van vele beschavingen en culturen. Het komt niet uit de hemel naar ons toe, een geschenk van de goden. Het is niet de creatie van een boekuitgever. Het is inderdaad zo menselijk als wij, net als de rest van de wiskunde. Achter elk symbool, formule en regel is een menselijk gezicht te vinden, of op zijn minst gezocht.
verder hopen we dat u nu een basis appreciatie hebt voor hoe interessant en divers getalsystemen kunnen worden., We zijn er vrij zeker van dat je ook begint te erkennen dat we ons eigen nummersysteem zo vanzelfsprekend vinden dat wanneer we proberen ons aan te passen aan andere systemen of bases, we onszelf echt moeten concentreren en nadenken over wat er aan de hand is.







