Elektromagnetisme | Physics For Idiots

voor elektromagnetisme alles wat je moet weten is wat er gebeurt als je + of – ladingen hebt, wat er gebeurt als ze dichtbij komen en wat er gebeurt als ze bewegen. Dat is het! Voor alle niet-kwantum EM zijn er slechts 5 formules die je nodig hebt.,de Lorentz vergelijking beschrijven van elektriciteit, magnetisme, licht, geluid, straling, eigenlijk de meeste van de fysica:

(1)

(2)

(3)

(4)

(5)

Hoe slecht kan een onderwerp worden als je het kan beschrijven allemaal met slechts 5 vergelijkingen, zou je waarschijnlijk passen ze allemaal op de rug van een beermat., Nu je de conclusie hebt gezien kunnen we naar het begin gaan en het hele verhaal in detail lezen. Tenzij je een universitaire cursus doet kun je wegkomen met het niet precies weten wat de vergelijking betekent of doen, maar deze site zal ze later uitleggen, laten we eerst terug naar de basis.

de basis

lading komt in 2 types, positief en negatief en wordt gemeten in Coulombs (C). Als je een lading op zijn eigen zendt het een veld in alle richtingen. Het veld van een lading wordt weergegeven door E zoals in E-lectriciteit., Als je een andere lading in het veld plaatst, ervaart het een kracht. Zoals ladingen afstoten en in tegenstelling tot ladingen aantrekken. Hoe groter de lading hoe sterker de kracht en hoe verder weg de ladingen hoe zwakker de kracht, precies wat je zou verwachten. Deze relatie kan worden weergegeven door Coulomb Wet;

De ’s zijn de twee ladingen en is de afstand tussen hen in het kwadraat., Het andere bit is gewoon een constante die ruwweg gelijk is aan 9000000000. (De exacte afleiding van deze wet is hier te vinden). Hieruit kun je zien dat de kracht gewoon de veldtijden is door welke lading je ook invoert, . Hiermee kun je het veld of de kracht bepalen tussen deeltjes of atomen of wat dan ook met lading, op voorwaarde dat ze niet bewegen. Zodra je een lading begint te verplaatsen, gebeuren er andere dingen.

Stuff Moving

zodra een lading begint te bewegen, produceert het een ander veld., Het nieuwe veld is magnetisme en wordt vertegenwoordigd door B zoals in B-magmatisme?

De reden dat het B is gewoon dat het was het tweede ding in een alfabetische lijst:

Elektromagnetische vector potentieel: Een
Magnetische inductie: B
Totale elektrische stroom: C
Elektrische verplaatsing: D
Elektromotorische kracht: E
Mechanische kracht: F
Snelheid op een punt: G
Magnetische intensiteit: H

(Dit verklaart ook waar H komt uit voor diegenen die geïnteresseerd zijn).,

dus nu heeft je deeltje of atoom of wat dan ook 2 velden die eruit komen. De volledige vergelijking om te beschrijven hoe beide velden inwerken op een deeltje is

die bekend staat als de lorentzkracht. Het symbool betekent geen vermenigvuldiging, in deze context betekent het Cross-Product. Het is in principe een korte manier om “ keer keer de sinus van de hoek tussen”te schrijven., Dit komt omdat het veld 90° naar welke richting het wijst en in welke richting je beweegt. Nu, tenzij je EM voorbij A-niveau doet, kun je alle richtingen en hoeken vergeten en gewoon

als we de bovenstaande uitdrukking uitvouwen hebben we

maar we kunnen al een van deze Bits beschrijven, is gewoon coulombs-wet., Op A-niveau of lager zal de situatie waarschijnlijk vereenvoudigd worden, zodat u alleen de velden en afzonderlijk hoeft te bekijken., Je zal dus waarschijnlijk enkel gebruik maken van één van de volgende twee formules,

Natuurlijk is de kracht en is belast, en zijn de twee velden eerder beschreven en is de snelheid van de bewegende lading., Het elektrische veld wordt gemeten in de SI-eenheden Newton per coulomb () of, gelijkwaardig, volt per meter (). Het magnetisch veld heeft de SI-eenheden van Tesla ‘ s (T), gelijk aan Webers per vierkante meter () of Volt-seconden per vierkante meter ()

Circuits

nu ben ik geen grote fan van circuits, nooit geweest, nu hopelijk zal ik wees professioneel genoeg dat mijn afkeer van hen niet zal komen over in deze sectie, maar als het wel mijn excuses op voorhand., Als ik echt met mijn haat begin te worstelen, moet ik misschien een tweede schrijver

een circuits zijn in principe gewoon een reeks bewegende ladingen met een occasioneel object of apparaat op de manier die de stroom beïnvloedt. Als Ik zeg dat de elektronen rond bewegen zullen de meeste mensen denken dat hun snelheid dicht bij de lichtsnelheid ligt, maar dit is verkeerd. De elektronen bewegen extreem langzaam, het is de golf die snel reist. Zoals hierboven vermeld stoten ladingen af, dus zet het ene elektron naast het andere en ze zullen uit elkaar bewegen., Met een stroom in een draad heb je in principe een buis van elektronen en je voegt er een toe aan een van de uiteinden, dit zorgt ervoor dat het volgende elektron naar beneden beweegt wat op zijn beurt het volgende elektron duwde enzovoort. Je hebt dus een Mexicaans golfachtig effect dat snel beweegt, maar de elektronen zelf bewegen slechts langzaam.

Circuits bevatten meestal allerlei verschillende objecten en apparaten, afhankelijk van waar ze voor zijn, en afhankelijk van hoe je ze allemaal in het circuit instelt, hangt af van hoe je al je berekeningen doet.

welke is welke?,

Als je al je componenten in een gesloten lus zoals so

dan zeggen we dat alle componenten in serie zijn. Als je ze instelt met branching paden zoals so

dan zeggen we dat de componenten Parallel zijn. U kunt ook circuits maken die een mengsel zijn van series en parallelle secties zoals so

versterkers, Volt en Ohm (Oh my!,)

we noemen de bewegende ladingen een stroom, en het wordt gemeten in de SI-eenheid van Amps (A). Amps zijn gelijk aan de hoeveelheid lading die in een bepaalde tijd wordt doorgegeven, dus 2 coulombs in 6 seconden zullen gelijk zijn aan 0,3 A. Dit, zoals de meeste dingen in de natuurkunde kunnen worden uitgedrukt in een mooie formule voor u om te leren

een ander belangrijk idee in circuits is spanning of potentiaalverschil. Volt is in principe het verschil in de elektrische potentiaal op twee verschillende punten., De elektrische potentiaal tussen 2 punten wordt gegeven als

waarbij de afstand is tussen en . Het is in principe veld keer afstand.

een ander belangrijk idee als het gaat om circuits is weerstand. Weerstand is in principe een maat van hoeveel weerstand tegen een elektrische stroom., Bijna alle objecten of apparaten in een circuit veroorzaken weerstand en voor het berekenen van de totale weerstand in een circuit gebruik je één of meer van deze regels

Eén van de belangrijkste en meest fundamentele vergelijkingen in circuits is de wet van Ohm, en het relateert stroom, spanning en weerstand.

The Deep End

Dit is het. Klassieke EM gaat niet dieper dan dit., Deze 4 zijn de fundamentele vergelijking voor alle velden in EM. Ze kunnen een beetje nodig hebben om je hoofd rond te krijgen, maar als je het eenmaal doet moet het allemaal zinvol zijn, een soort van.,

Als je niet weet over integratie en differentiatie, ik stel voor dat je hoofd naar de Integratie van de sectie of de Differentiatie punt, ik zal het proberen uit te leggen hier, maar ik zal vooral worden gericht op de fysica.

Gauss ‘wet

Ok dan hebben we eerst Gauss’ wet.,

Dit zegt dat de integraal van het elektrische veld, , door een gesloten gebied gelijk is aan de totale lading binnen het gebied, gedeeld door . is een constante die de permittiviteit van vrije ruimte wordt genoemd en verschijnt in de hele Natuurkunde samen met wat de permeabiliteit van vrije ruimte is., Wat deze vergelijking betekent is dat je elk gesloten oppervlak kunt nemen dat je wilt en het veld kunt vinden dat doorloopt, mits je de wiskunde kunt doen. Meestal kun je niet. maar er zijn een aantal gevallen wanneer het leuk en gemakkelijk. Gevallen waarin het veld recht door het oppervlak komt., De gevallen zijn

een bolvormig oppervlak rond een punt of bol
een cilindrisch oppervlak rond een oneindige draad
Een regelmatig oppervlak over een deel van een oneindig vlak

Ik geef toe dat dit vaag en abstract klinkt, dus Ik zal het demonstreren met behulp van een diagram.

Dit zijn de Gaussische oppervlakken., Met deze oppervlakken probeer je het leven makkelijker te maken. Je zorgt er alleen voor dat het oppervlak altijd op dezelfde afstand van de ladingsbron is en dat het veld altijd door gaat bij 90 graden. U kunt dan werken uit de integraal met je ogen gesloten zijn dat gemakkelijk. De linkerkant van Gauss ‘ wet wordt E keer het oppervlak van de vorm die u koos.

een bolvormig oppervlak wordt , waarbij de straal van de bol is.,
een cilindrisch oppervlak wordt , waarbij en de lengte en de straal van de cilinder zijn.
een normaal oppervlak wordt , waarbij het gebied boven en onder het oneindige oppervlak is (je hebt de factor 2 nodig als het veld boven en onder het oppervlak gaat bij 90 graden).,

So Gauss’ law for a sphere becomes

Which was introduces earlier as Coulombs Law, now you know where it came from., Gauss’ Wet voor een oneindige lijn van betaling is alleen

dit Nu iets nieuws geïntroduceerd . Als je een oneindige ladingslijn hebt dan is de totale lading daarop oneindig en er is geen manier om te weten hoeveel van die oneindige lading je in je Gaussiaanse oppervlak zou hebben., Dat is waar komt, het is een waarde van lading per lengte-eenheid, dus als =4Cm en je hebt 5 meter dan is de lading gewoon 20C. dat is alles is, slechts een waarde van lading.

voor een oneindig oppervlak wordt de wet van gauss

opnieuw is er een nieuw symbool toegevoegd, maar het is net als voorheen., is alleen de lading per oppervlakte-eenheid, dus als =5Cm en u een 100m oppervlakte hebt, is de totale lading 500C.

geladen Ring

laten we zeggen dat je een opgeladen ring hebt en je moet weten welk veld er uit voortkomt. Opnieuw zullen we een van de belangrijkste instrumenten in de natuurkunde gebruiken, om dingen makkelijker te maken. Ten eerste zullen we alleen kijken naar het veld langs de as van de ring, anders dingen gewoon te ingewikkeld en het is niet de moeite waard., Laten we nu een heel klein deel van de ring nemen en zeggen dat het een bol is. Dit is niet echt waar, maar hoe kleiner we maken de sectie Hoe meer we kunnen maken het lijkt op een punt lading. Dus je hebt iets als dit

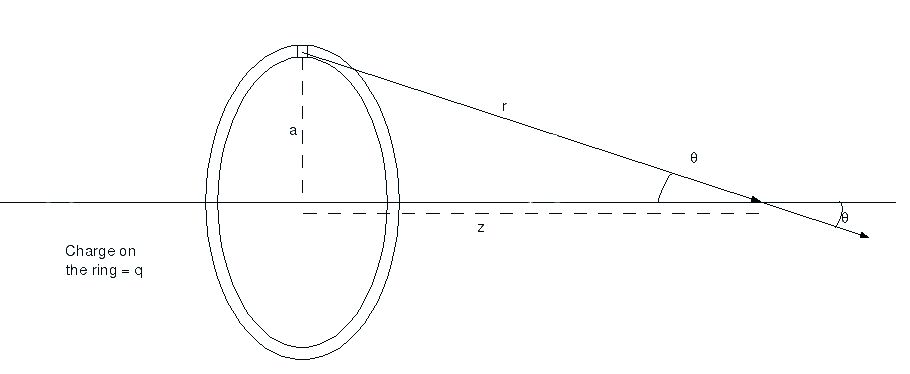
u wilt het veld vinden op een punt langs de as van de ring van de totale lading en radius . Het kleine vierkantje bovenaan, dat is het deel waarvan je aanneemt dat het een geladen bol is., Nu weten we niet hoeveel lading er in dat kleine gedeelte zit omdat je het elke gewenste grootte kunt maken, dus noemen we gewoon de lading , een kleine hoeveelheid van . Dus we hebben nu

als je erover nadenkt, zal elk bit van de ring boven de as die naar beneden duwt een gelijk bit hebben onder de as die omhoog duwt. Het zal ook hetzelfde zijn voor links en rechts en alle andere delen van de ring., Dus alle kracht van de ring zal alleen werken langs de as. Om alleen dit deel uit te werken moeten we wat trig gebruiken. We moeten het veld vermenigvuldigen met om de axiale component te krijgen.,

As you may or may not know can also be described (using SOH CAH TOA) by the following relationship for our situation

As is the adjacent side and is the hypotenuse., Dus nu hebben we

hoewel we misschien niet weten wat is. We kennen wel de straal van de schijf, , en de afstand die we tot de schijf hebben, .,is

Nu we willen om zich te ontdoen van dat , zo integreren we

Nu weten we uit het schema aan het begin dat de totale kosten op de schijf , dus als we alle kleine beetjes de totale moet , zodat de integraal is gewoon .,

div id=”60615e2290″> veld van een opgeladen schijf. Alles wat je nodig hebt is het veld van een punt en wat trig kennis en je kunt het uitwerken. Ik had je gewoon de uiteindelijke oplossing kunnen geven, maar op deze manier kun je zien waar het vandaan kwam en als je het vergeet, kun je het misschien uitwerken vanuit de eerste principes zoals hierboven.,

Gauss ‘ wet voor magnetisme

deze is mooi en eenvoudig, maar heeft een aantal grote implicaties. Gauss ‘ wet voor magnetisme is

Het is net als de gewone Gauss’ wet in die zin dat het een veld beschrijft, ditmaal het magnetische veld, . Het zegt dat de integraal van B over een gesloten oppervlak, nul is. Niets. Elke veldlijn die uit het oppervlak gaat heeft een equivalent dat erin gaat. Er is geen algemeen veld., Dit betekent dat het onmogelijk om bronnen van magnetisch veld te krijgen. Terwijl elektronen en protonen de oorsprong van het veld zijn, waarvan de veldlijnen afwijken van of convergeren naar, is er geen magnetisch analoog. Magnetische veldlijnen zijn altijd gesloten lussen, geen begin, geen einde. Dit weerhield mensen er natuurlijk niet van zich voor te bereiden voor het geval we een magnetische monopole vinden.

deze vergelijking lijkt misschien leuk, en dat is het ook, maar het is volkomen nutteloos op zichzelf., Meestal is een 0 resultaat in de natuurkunde heel belangrijk, het betekent dat er iets speciaals gebeurt, hier toont het aan dat magnetische monopolen niet bestaan.

Faradays Law

nu worden de zaken complexer, hier hebben we Faradays law,

ik loop met je mee door elk stukje om je te laten zien wat het eigenlijk betekent. Eerst hebben we de linkerkant die gemakkelijk is. Het is net als Gauss ‘ wet alleen de integraal is over een ander ding., In plaats van het totale veld door een oppervlak te vinden, , vinden we nu het totale veld rond een gesloten lus . Dat is alles wat anders is met de linkerkant, geen oppervlakken meer, alleen gesloten lussen. Nu naar de rechterkant. Ten eerste hebben we een min, en noteert ingewikkeld daarover. Waarom zijn er zal later worden uitgelegd. Vervolgens hebben we nog een integraal, en deze ziet er verschrikkelijk uit. Het symbool betekent in principe een kleine verandering., Dus is een verandering in , en is een verandering in , waarbij is tijd. De hele is de mate van verandering van , Het is hoeveel verandert () in een bepaalde tijd (). En dat wordt geïntegreerd over een gebied ., is het gebied binnen de gesloten lus , als je een willekeurig kronkelend ding tekent om er zeker van te zijn dat de lijn zichzelf niet kruist en dat het zichzelf verbindt dan is de lengte rond de lijn jouw en het gebied binnen de lijn jouw . Simpel ja? Dus het totaal rond een lus is gelijk aan de min van de wisselende door de lus.

Wat gebeurt er als er geen is?, Er is geen dus is nul, wat de integraal 0 maakt, dus geen . Wat gebeurt er als u een constante hebt? Nogmaals is 0. Dus is nul, wat de integraal 0 maakt, dus nogmaals geen . U kunt alleen een veld induceren uit een veranderend veld.,

het belang van het minteken komt voort uit het feit dat velden create velden en velden create velden (zoals getoond in de wetten van Faraday en Ampere). Als de Min er niet was dan zouden de velden gewoon blijven bouwen en bouwen en uiteindelijk oneindige energie geven, en dat is niet toegestaan!

Ampère-Maxwell Law

de laatste van Maxwell ‘ s vergelijkingen is de Ampere-Maxwell law., Net als de eerste twee wetten waren vergelijkbaar, dus zijn de laatste twee, Er is een patroon aan hen in deze volgorde die ze gemakkelijker te onthouden kan maken. over een gebied, over een gebied, rond een lus en nu ten slotte rond een lus. De vergelijking is

linkerkant, gemakkelijk, integraal van B rond een gesloten lus. Rechts, niet zo makkelijk., Laten we eerst de bit negeren, daar kom ik nog op terug. Anders dan de lijkt het sterk op de Faradays-wet. U hebt een ander veranderend veld geÃ ntegreerd over een gebied, maar dit keer is het . Deze keer echter, in plaats van te vermenigvuldigen met min 1, vermenigvuldig je met . Opnieuw zijn dit twee zeer belangrijke waarden in de fysica, alleen en gecombineerd. Zij vormen het hart van EM., Dus je magnetisch veld rond een lus is net gelijk aan het veranderende e veld dat het keer doorloopt met , maar dan moet je nog een beetje toevoegen. Dit is de bit. Dit is gewoon de stroom die rond de lus gaat met , dit is omdat, zoals gezegd in bewegende dingen, als je een bewegende lading hebt, dat wil zeggen een stroom, dan krijg je een magnetisch veld. Dus je moet de twee bits bij elkaar optellen. Zo, klaar.,

Andere Vorm van de Diepe

Als het schrijven van de vergelijkingen van Maxwell boven, in de zogenaamde integrale vorm, u kunt ook schrijven ze in differentiële vorm zoals

Nog een Andere Vorm van het Diepe

Schrijven van de vergelijkingen van Maxwell in één van de twee bovenstaande vormen is echt een vereenvoudiging., Zowel de integraalvorm als de differentiaalvorm zijn vectorvergelijkingen en ze besparen u om de volledige 8 Maxwell-vergelijkingen uit te schrijven voor de velden en in alle drie dimensies.,div id=”a2ea6619e6″>

Well iot turns out you can also compactify the four vector Maxwell equations into two tensor equations like so

Here is a vector with four components, sometimes called the 4-current, and is a 4×4 matrix called the electromagnetic tensor., Ze worden gedefinieerd als

(6)

(7)

waarbij de lichtsnelheid is. De en vertellen u gewoon waar in de vector of matrix te zoeken, maar verwarrend voor sommige beginnen bij 0, dus en (niet te verwarren met tot de bodem). Hetzelfde met , dus en