wanneer een “normale” fractie breuken in de teller of noemer of beide bevat, dan beschouwen we het als een complexe fractie. Dit type fractie is ook bekend als een samengestelde fractie.
Er worden twee methoden gebruikt om een dergelijke breuk te vereenvoudigen.
Methode 1
belangrijke stappen:
- Creëer een enkele breuk in de teller en noemer.,
- Pas de delingsregel van breuken toe door de teller te vermenigvuldigen met de reciproque of inverse van de noemer.
- zo nodig vereenvoudigen.
Methode 2
belangrijke stappen:
- Zoek de kleinste gemene deler (LCD) van alle noemers in de complexe fracties.
- vermenigvuldig dit LCD met de teller en noemer van de complexe fractie.
- zo nodig vereenvoudigen.,
na het doornemen van een paar voorbeelden, zou je je moeten realiseren dat Methode 2 veel beter is dan Methode 1 omdat het bijna altijd minder stappen vergt om tot het uiteindelijke antwoord te komen.
voorbeelden van het vereenvoudigen van complexe fracties
Voorbeeld 1: Vereenvoudig de complexe fractie hieronder.
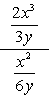
- volgens methode 1
zowel de teller als de noemer van de complexe fractie worden al uitgedrukt als afzonderlijke fracties. Dit is geweldig!,

de volgende stap is het toepassen van de delingsregel door de teller te vermenigvuldigen met de reciproque van de noemer. Eindig door het opheffen van gemeenschappelijke factoren om het definitieve antwoord te krijgen.
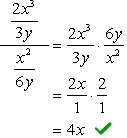
- Met behulp van Methode 2
zoek het LCD-scherm van het gehele probleem, dat wil zeggen het LCD-scherm van de bovenste en onderste noemers.,

aangezien het LCD van 3y en 6y gewoon \textbf{6y} is, zullen we nu de complexe teller en noemer vermenigvuldigen met dit LCD. Na dit te hebben gedaan, kunnen we verwachten dat het probleem wordt teruggebracht tot een enkele fractie die zoals gewoonlijk kan worden vereenvoudigd.
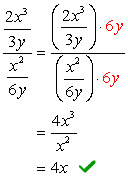
Voorbeeld 2: Vereenvoudig de complexe fractie hieronder.,
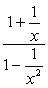
- Met behulp van Methode 1
in deze methode willen we een enkele breuk maken, zowel in de teller als in de noemer. Dit probleem vereist natuurlijk dat we dat eerst doen voordat we verdelen.
tel de breuken in de teller op en trek de breuken in de noemer af.,
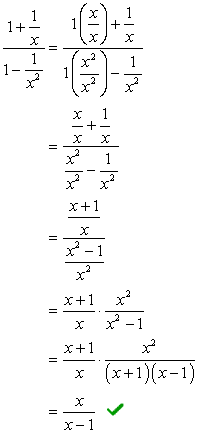
- Met behulp van Methode 2
kijkend naar de noemers \large{x} en \large{x^2}, moet het LCD-scherm \large{x^2} zijn} vermenigvuldig de boven-en onderkant met dit lcd.
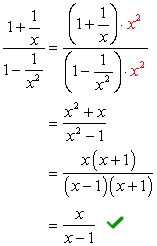
Voorbeeld 3: Vereenvoudig de complexe fractie hieronder.,
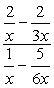
- Met behulp van Methode 1
maak afzonderlijke breuken in zowel de teller als de noemer, en vervolgens door de breuken te delen.
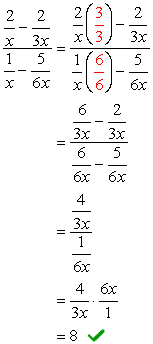
- Met behulp van Methode 2
het totale LCD-scherm van de noemers is \color{red}6x. gebruik dit om te vermenigvuldigen met de bovenste en onderste expressies.,
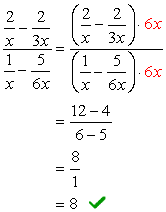
Voorbeeld 4: Vereenvoudig de complexe fractie hieronder.
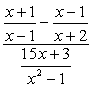
voor dit probleem gebruiken we alleen methode 1.
het probleem vereist dat u de FOLIEMETHODE (vermenigvuldiging van twee binomials) en een eenvoudige factorisatie van trinomial toepast. Het lijkt misschien een beetje intimiderend op het eerste; echter, als je aandacht besteden aan details, ik garandeer u dat het niet zo slecht.,
als je ziet, is de complexe noemer al in de vorm die we willen – met één fractioneel symbool. Dit betekent dat we een beetje moeten werken aan de complexe teller. Onze volgende stap zou zijn om de complexe teller om te zetten in een “eenvoudige” of enkele breuk.
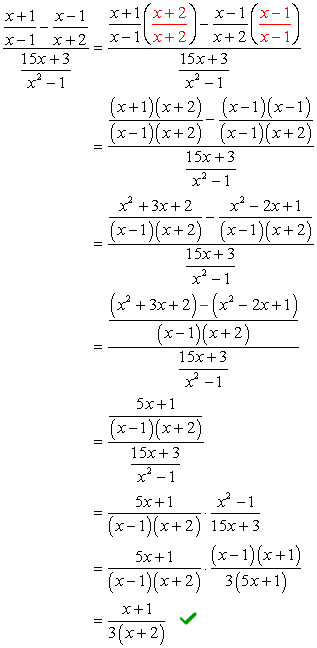
Voorbeeld 5: Vereenvoudig de complexe fractie hieronder.
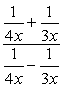
voor dit probleem zullen we alleen methode 2 gebruiken.,
merk op dat het LCD van alle noemers gewoon \color{red}12x is. gebruik dit als de gemeenschappelijke vermenigvuldiger voor zowel boven-als onderuitdrukkingen.
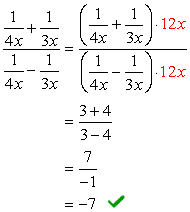
praktijk met werkbladen
u bent wellicht ook geïnteresseerd in:
vermenigvuldigen van complexe fracties
delen van complexe getallen