the 5 Clustering Algorithms data Scientists Need to Know

Ik ben onlangs begonnen met een educatieve nieuwsbrief gericht op boeken. Book Dives is een tweewekelijkse nieuwsbrief waar we voor elk nieuw nummer duiken in een non-fictie boek. Je leert over de kernlessen van het boek en hoe je ze in het echte leven kunt toepassen. U kunt zich hier voor inschrijven.

Clustering is een Machine Learning techniek waarbij datapunten worden gegroepeerd. Gegeven een set van datapunten, kunnen we een clustering algoritme gebruiken om elk datapunt in een specifieke groep te classificeren., In theorie zouden datapunten die in dezelfde groep zitten vergelijkbare eigenschappen en/of eigenschappen moeten hebben, terwijl datapunten in verschillende groepen zeer ongelijke eigenschappen en/of eigenschappen zouden moeten hebben. Clustering is een methode om zonder toezicht te leren en is een gemeenschappelijke techniek voor statistische gegevensanalyse die op vele gebieden wordt gebruikt.

In Data Science kunnen we clustering analyse gebruiken om waardevolle inzichten uit onze data te verkrijgen door te zien in welke groepen de datapunten vallen wanneer we een clustering algoritme toepassen., Vandaag gaan we kijken naar 5 populaire clustering algoritmes die data wetenschappers moeten weten en hun voor-en nadelen!

K-Means Clustering

K-Means is waarschijnlijk het meest bekende clustering algoritme. Het wordt onderwezen in een heleboel inleidende data science en machine learning klassen. Het is gemakkelijk te begrijpen en te implementeren in code! Bekijk de afbeelding hieronder voor een illustratie.,

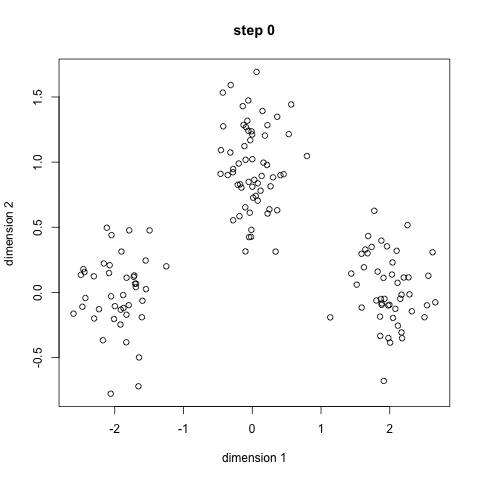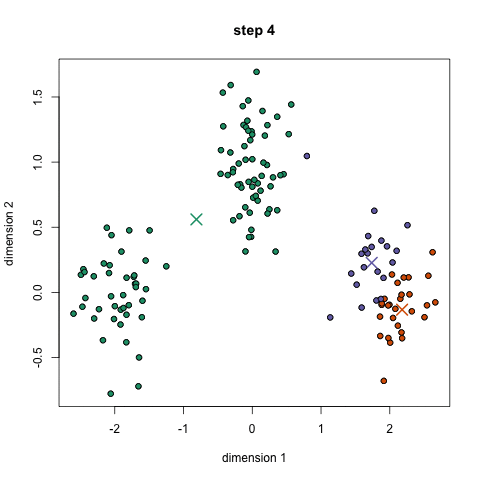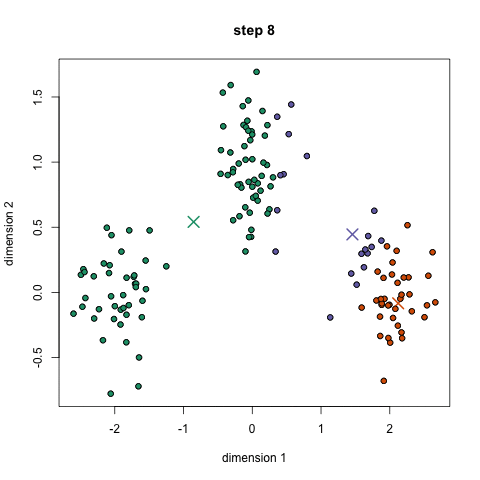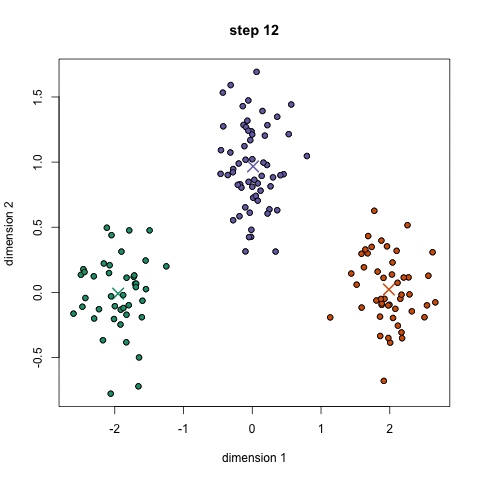
1. om te beginnen, selecteren we eerst een aantal klassen/groepen om te gebruiken en initialiseren willekeurig hun respectievelijke middenpunten. Om erachter te komen het aantal klassen te gebruiken, is het goed om een snelle blik op de gegevens te nemen en proberen om verschillende groeperingen te identificeren. De centrumpunten zijn vectoren van dezelfde lengte als elke datapuntvector en zijn de ” X ‘ s ” in de afbeelding hierboven.,
2. elk gegevenspunt wordt geclassificeerd door de afstand tussen dat punt en elk groepscentrum te berekenen, en vervolgens het punt te classificeren in de groep waarvan het centrum het dichtst bij het is.
3. op basis van deze geclassificeerde punten herberekenen we het groepscentrum door het gemiddelde van alle vectoren in de groep te nemen.
4. herhaal deze stappen voor een bepaald aantal herhalingen of totdat de groepscentra niet veel veranderen tussen herhalingen. U kunt er ook voor kiezen om de groepscentra een paar keer willekeurig te initialiseren en vervolgens de run te selecteren die eruit ziet alsof het de beste resultaten heeft opgeleverd.,

K-Means heeft het voordeel dat het vrij snel is, omdat we eigenlijk alleen de afstanden tussen punten en groepscentra berekenen; zeer weinig berekeningen! Het heeft dus een lineaire complexiteit O (n).

aan de andere kant heeft K-Means een paar nadelen. Ten eerste moet je selecteren hoeveel groepen/klassen er zijn. Dit is niet altijd triviaal en idealiter met een clustering algoritme zouden we willen dat het erachter te komen die voor ons omdat het doel van het is om wat inzicht te krijgen uit de gegevens., K-middelen begint ook met een willekeurige keuze van clustercentra en daarom kan het verschillende clustering resultaten op verschillende runs van het algoritme opleveren. Zo kunnen de resultaten niet herhaalbaar en gebrek aan consistentie. Andere clustermethoden zijn consistenter.

K-Medians is een ander clustering algoritme gerelateerd aan K-Means, behalve in plaats van de groepscentrumpunten te herberekenen met behulp van het gemiddelde gebruiken we de mediaan vector van de groep., Deze methode is minder gevoelig voor uitschieters (vanwege het gebruik van de mediaan) maar is veel langzamer voor grotere datasets omdat sortering vereist is bij elke iteratie bij het berekenen van de Mediaanvector.

Mean-Shift Clustering

Mean-Shift clustering is een algoritme gebaseerd op schuifvensters dat dichte gebieden van datapunten probeert te vinden. Het is een centroid-gebaseerd algoritme wat betekent dat het doel is om de centrumpunten van elke groep/klasse te lokaliseren, die werkt door kandidaten voor centrumpunten bij te werken om het gemiddelde van de punten binnen het schuifvenster te zijn., Deze kandidaat-vensters worden dan gefilterd in een post-processing fase om bijna-duplicaten te elimineren, die de definitieve reeks van centrumpunten en hun overeenkomstige groepen vormen. Bekijk de afbeelding hieronder voor een illustratie.

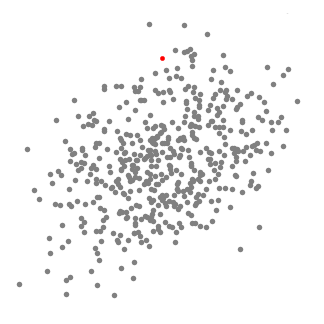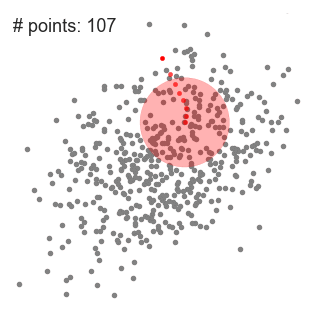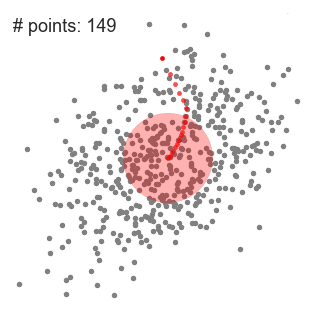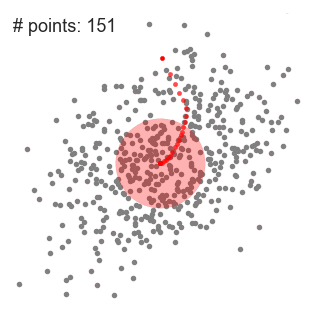
1. het leggen van de gemiddelde verschuiving wij beschouwen een reeks van punten in de twee-dimensionale ruimte, zoals op de illustratie hierboven., We beginnen met een cirkelvormig schuifraam gecentreerd op een punt C (willekeurig geselecteerd) en met radius r als kernel. Mean shift is een hill-climbing algoritme dat inhoudt dat deze kernel iteratief wordt verplaatst naar een hogere dichtheid regio op elke stap tot convergentie.
2. bij elke iteratie wordt het schuifvenster verschoven naar gebieden met een hogere dichtheid door het middelpunt te verschuiven naar het gemiddelde van de punten binnen het venster (vandaar de naam). De dichtheid binnen het schuifraam is evenredig met het aantal punten erin., Natuurlijk, door te verschuiven naar het gemiddelde van de punten in het venster zal het geleidelijk bewegen naar gebieden met een hogere puntdichtheid.
3. We gaan door met het verschuiven van het schuifvenster volgens het gemiddelde totdat er geen richting is waarin een shift meer punten in de kernel kan plaatsen. Bekijk de afbeelding hierboven; we blijven de cirkel bewegen totdat we de dichtheid niet meer verhogen (dat wil zeggen het aantal punten in het venster).
4. dit proces van stappen 1 tot en met 3 wordt gedaan met veel schuifvensters totdat alle punten binnen een venster liggen., Wanneer meerdere schuifvensters elkaar overlappen, wordt het raam met de meeste punten bewaard. De datapunten worden vervolgens geclusterd volgens het schuifraam waarin ze zich bevinden.

een illustratie van het gehele proces van end-to-end met alle schuifvensters wordt hieronder getoond. Elke zwarte stip vertegenwoordigt het middelpunt van een schuifraam en elke grijze stip is een gegevenspunt.,

in tegenstelling tot k-means clustering, is het niet nodig om het aantal clusters te selecteren omdat Mean-Shift dit automatisch ontdekt. Dat is een enorm voordeel. Het feit dat de clustercentra convergeren naar de punten van maximale dichtheid is ook heel wenselijk omdat het heel intuïtief te begrijpen is en goed past in een natuurlijk data-gedreven betekenis., Het nadeel is dat de selectie van de venstergrootte / straal ” r ” niet-triviaal kan zijn.

Dichtheidsgebaseerde ruimtelijke Clustering van toepassingen met ruis (DBSCAN)

DBSCAN is een dichtheidsgebaseerd geclusterd algoritme dat vergelijkbaar is met mean-shift, maar met een aantal opmerkelijke voordelen. Bekijk een andere mooie afbeelding hieronder en laten we beginnen!,

1. dbscan begint met een willekeurig startpunt dat niet is bezocht. De buurt van dit punt wordt geëxtraheerd met behulp van een afstand Epsilon ε (alle punten die binnen de ε afstand zijn buurtpunten).,
2. als er een voldoende aantal punten (volgens minPoints) binnen deze buurt zijn, start het clustering proces en wordt het huidige gegevenspunt het eerste punt in het nieuwe cluster. Anders zal het punt worden gelabeld als ruis (later kan dit lawaaierige punt het deel van het cluster worden). In beide gevallen wordt dat punt gemarkeerd als”bezocht”.
3. voor dit eerste punt in de nieuwe cluster worden de punten binnen de ε-afstandsbuurt ook deel van hetzelfde cluster., Deze procedure om alle punten in de ε-buurt tot hetzelfde cluster te maken, wordt vervolgens herhaald voor alle nieuwe punten die zojuist aan de clustergroep zijn toegevoegd.
4. dit proces van stappen 2 en 3 wordt herhaald totdat alle punten in het cluster zijn bepaald, d.w.z. alle punten binnen de ε-buurt van het cluster zijn bezocht en gelabeld.
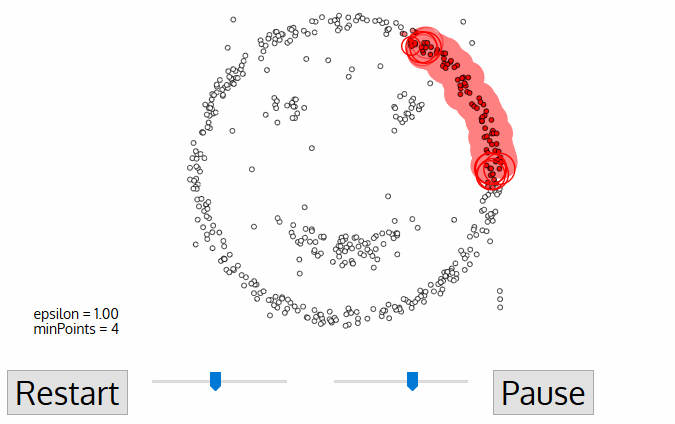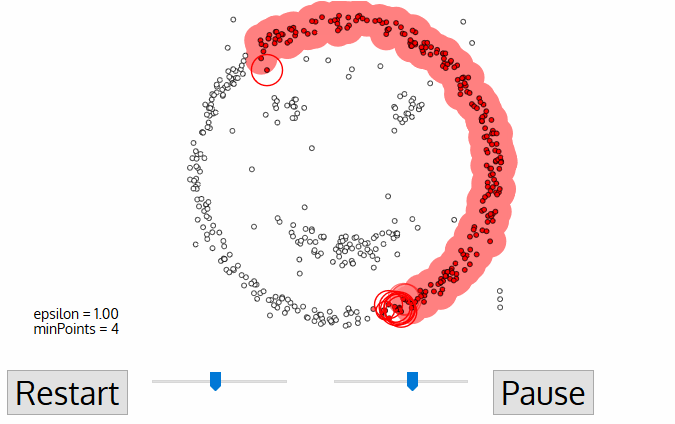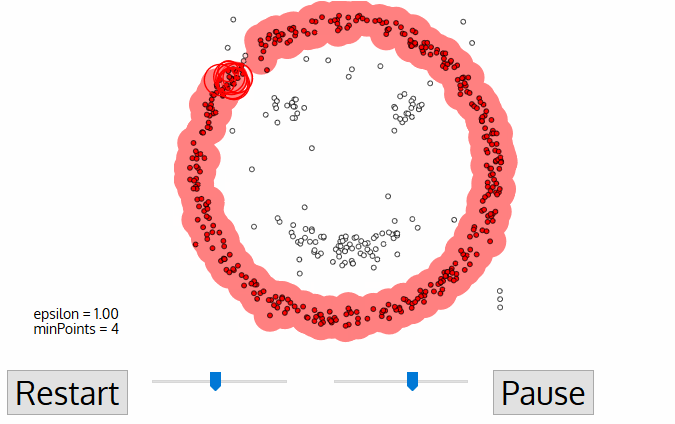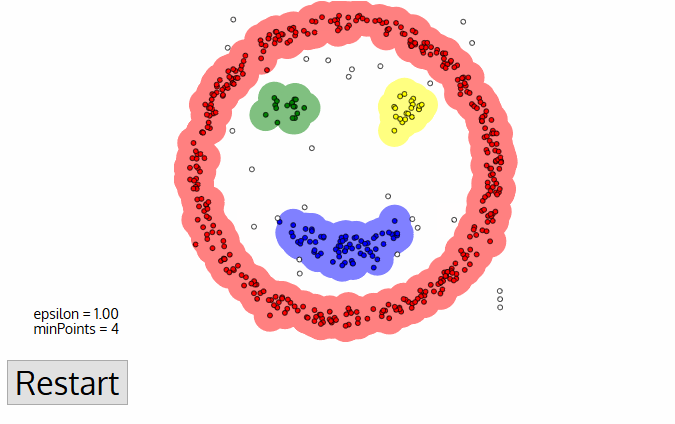
5. zodra we klaar zijn met het huidige cluster, wordt een nieuw niet-bezocht punt opgehaald en verwerkt, wat leidt tot de ontdekking van een ander cluster of ruis. Dit proces herhaalt zich totdat alle punten zijn gemarkeerd als bezocht., Aangezien aan het einde van dit alles alle punten zijn bezocht, zal elk punt zijn gemarkeerd als behorend tot een cluster of als ruis.

DBSCAN biedt enkele grote voordelen ten opzichte van andere clustering algoritmen. Ten eerste vereist het helemaal geen pe-set aantal clusters. Het identificeert uitschieters ook als geluiden, in tegenstelling tot mean-shift die ze gewoon in een cluster gooit, zelfs als het gegevenspunt heel anders is. Bovendien, het kan willekeurig formaat en willekeurig gevormde clusters heel goed vinden.,

het grootste nadeel van DBSCAN is dat het niet zo goed presteert als anderen wanneer de clusters van verschillende dichtheid zijn. Dit komt omdat de instelling van de afstandsdrempel ε en minPoints voor het identificeren van de buurtpunten zal variëren van cluster tot cluster wanneer de dichtheid varieert. Dit nadeel doet zich ook voor met zeer hoog-dimensionale gegevens, omdat opnieuw de afstandsdrempel ε moeilijk te schatten wordt.,

Expectation-Maximization (EM) Clustering met behulp van Gaussian Mixture Models (GMM)

een van de belangrijkste nadelen van K-Means is het naïeve gebruik van de gemiddelde waarde voor het clustercentrum. We kunnen zien waarom dit is niet de beste manier om dingen te doen door te kijken naar de afbeelding hieronder. Aan de linkerkant, lijkt het voor het menselijk oog heel duidelijk dat er twee cirkelvormige clusters met verschillende straal’ gecentreerd op hetzelfde gemiddelde. K-Means kan dit niet aan omdat de gemiddelde waarden van de clusters zeer dicht bij elkaar liggen., K-middelen falen ook in gevallen waar de clusters niet cirkelvormig zijn, opnieuw als gevolg van het gebruik van het gemiddelde als clustercentrum.

Gaussiaanse mengmodellen (GGM ‘ s) geven ons meer flexibiliteit dan k-means. Bij GGM ‘ s gaan we ervan uit dat de datapunten Gaussiaans verdeeld zijn; dit is een minder restrictieve aanname dan zeggen dat ze cirkelvormig zijn met behulp van het gemiddelde., Op die manier hebben we twee parameters om de vorm van de clusters te beschrijven: het gemiddelde en de standaardafwijking! Als we een voorbeeld nemen in twee dimensies, betekent dit dat de clusters elke vorm van elliptische vorm kunnen aannemen (aangezien we een standaardafwijking hebben in zowel de x-als de Y-richting). Zo wordt elke Gaussiaanse distributie toegewezen aan een enkele cluster.

om de parameters van de Gaussian voor elke cluster te vinden (bijvoorbeeld de gemiddelde en standaardafwijking), gebruiken we een optimalisatiealgoritme genaamd Expectation–Maximization (EM)., Neem een kijkje op de afbeelding hieronder als een illustratie van de Gaussianen worden aangepast aan de clusters. Dan kunnen we doorgaan met het proces van verwachting–maximalisatie clustering met GGM ‘ s.

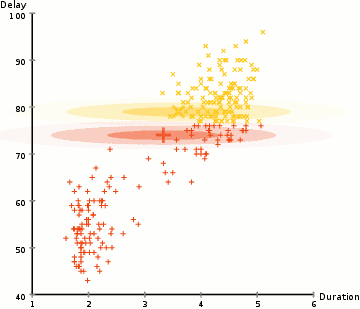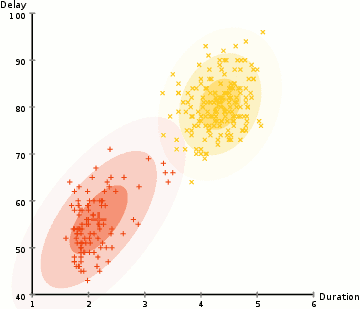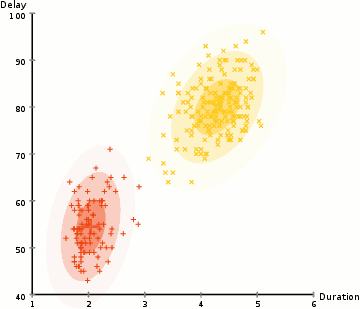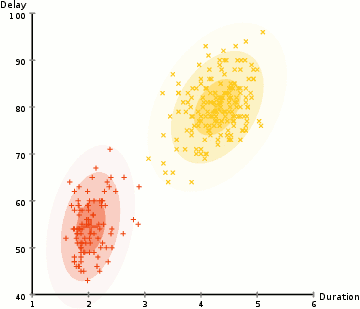
1. we beginnen met het selecteren van het aantal clusters (zoals K-Means doet) en willekeurig initialiseren van de Gaussiaanse distributieparameters voor elke cluster., Men kan proberen om een goede guesstimate voor de eerste parameters door het nemen van een snelle blik op de gegevens te bieden. Hoewel opmerking, zoals kan worden gezien in de afbeelding hierboven, Dit is niet 100% nodig als de Gaussianen beginnen onze Als zeer slecht, maar zijn snel geoptimaliseerd.
2. gegeven deze Gaussiaanse distributies voor elk cluster, bereken de waarschijnlijkheid dat elk gegevenspunt tot een bepaald cluster behoort. Hoe dichter een punt bij het centrum van de Gaussiaan is, hoe waarschijnlijker het tot die cluster behoort., Dit zou intuã tief zinvol moeten zijn aangezien met een Gaussiaanse distributie wij veronderstellen dat de meeste gegevens dichter bij het centrum van de cluster ligt.
3. op basis van deze waarschijnlijkheden berekenen we een nieuwe set parameters voor de Gaussiaanse distributies zodanig dat we de waarschijnlijkheid van datapunten binnen de clusters maximaliseren. We berekenen deze nieuwe parameters aan de hand van een gewogen som van de datapuntposities, waarbij de gewichten de waarschijnlijkheden zijn van het datapunt dat in dat bepaalde cluster hoort., Om dit visueel uit te leggen kunnen we een kijkje nemen op de afbeelding hierboven, in het bijzonder de gele cluster als voorbeeld. De distributie begint willekeurig bij de eerste iteratie, maar we kunnen zien dat de meeste gele punten rechts van die distributie liggen. Wanneer we een som berekenen gewogen door de waarschijnlijkheden, ook al zijn er een aantal punten in de buurt van het centrum, de meeste van hen zijn aan de rechterkant. Zo wordt het gemiddelde van de verdeling natuurlijk dichter bij die verzameling punten verschoven. We kunnen ook zien dat de meeste punten zijn “boven-rechts naar beneden-links”., Daarom verandert de standaardafwijking om een ellips te creëren die meer op deze punten is afgestemd, om de som gewogen door de waarschijnlijkheden te maximaliseren.
4. stappen 2 en 3 worden iteratief herhaald tot convergentie, waarbij de distributies niet veel veranderen van iteratie naar iteratie.

het gebruik van GGM ‘ s heeft 2 belangrijke voordelen. Ten eerste zijn GGM ‘ s veel flexibeler in termen van cluster covariantie dan K-middelen; vanwege de standaarddeviatieparameter kunnen de clusters elke ellipsvorm aannemen, in plaats van beperkt te zijn tot Cirkels., K-Means is eigenlijk een speciaal geval van GGM waarin de covariantie van elke cluster langs alle dimensies 0 nadert. Ten tweede, aangezien GGM ‘ s waarschijnlijkheden gebruiken, kunnen ze meerdere clusters per gegevenspunt hebben. Dus als een gegevenspunt zich in het midden van twee overlappende clusters bevindt, kunnen we eenvoudig zijn klasse definiëren door te zeggen dat het X-procent tot klasse 1 en Y-procent tot klasse 2 behoort. De GGM ‘ s steunen gemengd lidmaatschap.

Agglomeratieve hiërarchische Clustering

hiërarchische clustering algoritmen vallen in 2 categorieën: top-down of bottom-up., Bottom-up algoritmen behandelen elk gegevenspunt in het begin als een enkele cluster en vervolgens achtereenvolgens samenvoegen (of agglomereren) paren van clusters totdat alle clusters zijn samengevoegd tot een enkele cluster die alle gegevenspunten bevat. Bottom-up hiërarchische clustering wordt daarom hiërarchische agglomeratieve clustering of HAC genoemd. Deze hiërarchie van clusters wordt weergegeven als een boom (of dendrogram). De wortel van de boom is de unieke cluster die alle monsters verzamelt, de bladeren zijn de clusters met slechts één monster., Bekijk de afbeelding hieronder voor een afbeelding voordat u naar de algoritme stappen

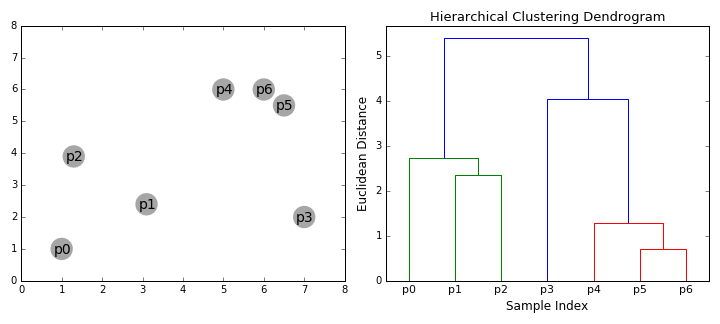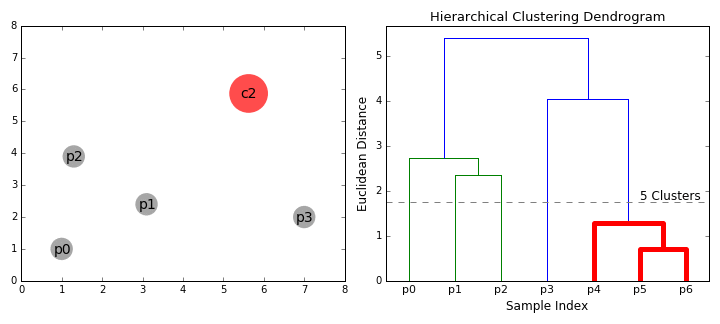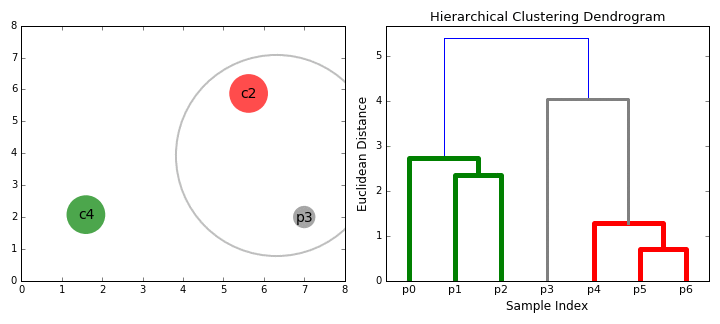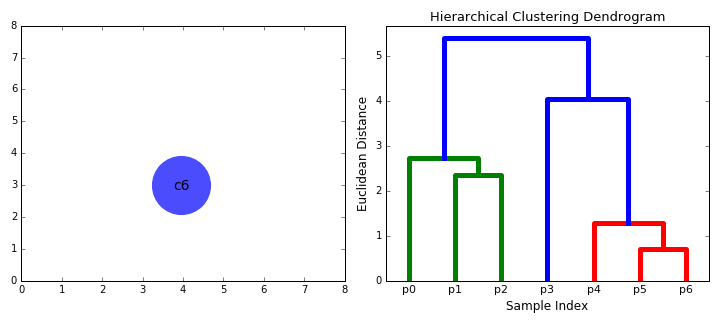
1. We beginnen met de behandeling van elk gegevenspunt weer als één cluster i.e als er X gegevenspunten in onze dataset dan hebben we X clusters. We selecteren vervolgens een afstandsmetriek die de afstand tussen twee clusters meet., Als voorbeeld zullen we de gemiddelde koppeling gebruiken die de afstand tussen twee clusters definieert als de gemiddelde afstand tussen gegevenspunten in het eerste cluster en gegevenspunten in het tweede cluster.
2. bij elke iteratie combineren we twee clusters in één. De twee te combineren clusters worden geselecteerd als die met de kleinste gemiddelde koppeling. Dat wil zeggen volgens onze geselecteerde afstandsmetriek, hebben deze twee clusters de kleinste afstand tussen elkaar en zijn daarom het meest vergelijkbaar en moeten worden gecombineerd.
3. Stap 2 wordt herhaald tot we de wortel van boom i bereiken.,e we hebben maar één cluster die alle datapunten bevat. Op deze manier kunnen we kiezen hoeveel clusters we uiteindelijk willen, simpelweg door te kiezen wanneer we stoppen met het combineren van de clusters dat wil zeggen wanneer we stoppen met het bouwen van de boom!

hiërarchische clustering vereist niet dat we het aantal clusters specificeren en we kunnen zelfs selecteren welk aantal clusters er het beste uitziet omdat we een boom aan het bouwen zijn. Bovendien is het algoritme niet gevoelig voor de keuze van afstandsmetriek; ze hebben allemaal de neiging om even goed te werken terwijl met andere clustering algoritmen, de keuze van afstandsmetriek cruciaal is., Een bijzonder goed gebruik van hiërarchische clustering methoden is wanneer de onderliggende data heeft een hiërarchische structuur en u wilt de hiërarchie te herstellen; andere clustering algoritmen kunnen dit niet doen. Deze voordelen van hiërarchische clustering gaan ten koste van een lagere efficiëntie, omdat het een tijdscomplexiteit van O(n3) heeft, in tegenstelling tot de lineaire complexiteit van K-middelen en GGM.