in de meetkunde is een veelvlak een figuur met gesloten ruimte waarvan de zijden polygonen zijn. Het woord polyhedron heeft Griekse oorsprong, wat betekent veel gezichten. Hieronder volgen enkele voorbeelden van veelvlakken.
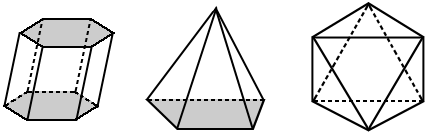
kenmerken van een veelvlak
de veelhoeken die een veelvlak vormen worden gezichten genoemd. De lijnsegmenten die door twee snijvlakken worden gecreëerd, worden randen genoemd. De hoekpunten zijn punten waar drie of meer randen samenkomen.,
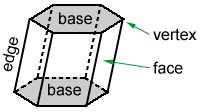
het hexagonale prisma hierboven is een veelvlak dat 6 zijvlakken heeft die parallelogrammen zijn, en 2 zijvlakken aan de boven-en onderkant, basen genaamd, die zeshoeken zijn.
de Stelling van Euler
De Stelling van Euler toont een relatie tussen het aantal vlakken, hoekpunten en randen van een veelvlak., Het stelt dat de som van de vlakken en hoekpunten minus het aantal randen altijd gelijk is aan twee:
F + V – e = 2
waarbij F het aantal vlakken is, V het aantal hoekpunten en E het aantal randen van een veelvlak.
voorbeeld:
voor het hierboven getoonde zeshoekige prisma, F = 8 (zes zijvlakken + twee basen), V = 12 en E = 18:
8 + 12 – 18 = 2
classificaties van veelvlakken
veelvlakken kunnen op vele manieren worden ingedeeld. Ze kunnen bijvoorbeeld worden geclassificeerd als regelmatige en onregelmatige veelvlakken., Een regelmatige veelvlak is een veelvlak waarvan de vlakken allemaal congruente regelmatige veelhoeken zijn; elke veelvlak dat niet aan deze voorwaarden voldoet wordt als onregelmatig beschouwd.
veelvlakken kunnen ook worden geclassificeerd als convex en concaaf. Een concave veelhoek heeft ten minste één zijde die een concave veelhoek is. Een veelvlak dat niet concaaf is, is convex. Veelvlakken kunnen ook worden geclassificeerd op basis van het aantal gezichten. Bijvoorbeeld, een tetraëder heeft 4 gezichten, een pentaëder heeft 5 gezichten, en een hexaëder heeft 6 gezichten.,
Hieronder volgt een lijst van termen die vaak worden gebruikt om veelvlakken te beschrijven op basis van hun kenmerken.
prisma ’s
prisma’ s zijn veelvlakken die twee congruente vlakken hebben, basen genoemd, die in parallelle vlakken liggen. Een prisma wordt typisch genoemd door de vorm van zijn veelhoekige basissen. De zijvlakken (de zijkanten die geen basen zijn) zijn parallelogrammen, rechthoeken of vierkanten.,
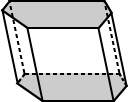
| regulier prisma | 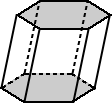 |
 |
|
|---|---|---|---|
| de bases voor de Regulier het hexagonale prisma hierboven heeft basissen die regelmatige zeshoeken zijn. | de basis voor het hexagonale prisma hierboven is onregelmatig hexagon. |
piramiden
piramiden zijn veelvlakken met een veelhoek als basis en driehoeken als alle andere vlakken.Een piramide wordt ook typisch genoemd door de vorm van zijn veelhoekige basis.,
| regelmatige piramide | onregelmatige piramide | 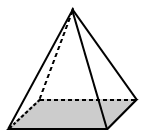 |
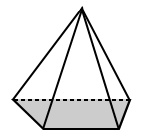 |
de basis van de vierkante piramide hierboven heeft een basis die is een vierkant (een regelmatige veelhoek). | de basis voor de trapeziumpiramide hierboven is een trapezium met ongelijke zijden (dus het is een onregelmatige veelhoek). |
|---|
regelmatige veelvlakken
een regelmatige veelvlakken is een veelvlakken waarvan alle zijden congruent zijn, regelmatige veelhoeken., Een regelmatige veelvlak wordt genoemd op basis van het aantal gezichten. Er zijn slechts vijf veelvlakken die regelmatige veelvlakken zijn; deze worden Platonische lichamen genoemd.
de vijf Platonische lichamen
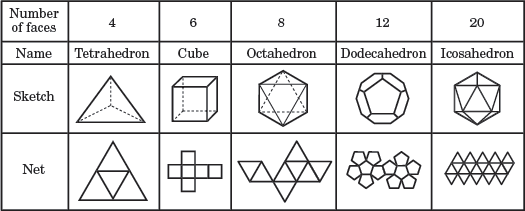
in het bovenstaande diagram wordt elke reguliere veelvlakte benoemd op basis van het aantal gezichten. Het net onder elke schets toont een 2D foto van alle gezichten van de veelvlakken.
De meeste reguliere prisma ‘ s worden over het algemeen niet als reguliere veelvlakken beschouwd., Een kubus is het enige reguliere prisma dat ook kan worden geclassificeerd als een regelmatige veelvlak.
evenzo is een regelmatige tetraëder de enige regelmatige piramide die ook een regelmatige veelvlak is.