Introduction to Philosophy: Logic (Português)

There’s an ancient view, still widely held, that what makes human beings special—what distinguises us from the “beasts of the field”—is that we are rational. Em que consiste a racionalidade? Essa é uma questão incómoda, mas uma possível resposta vai aproximadamente assim: nós manifestamos a nossa racionalidade por se envolver em atividades que envolvam o raciocínio, a tomada de declarações e cópias de segurança com razões, deliberando de acordo com razões e crenças, desenho inferências a partir de evidências disponíveis, e assim por diante.,

esta atividade de raciocínio pode ser bem feita e pode ser mal feita; pode ser feita corretamente ou incorretamente. A lógica é a disciplina que visa distinguir o bom raciocínio do mau.o bom raciocínio não é necessariamente eficaz. De facto, como veremos num capítulo subsequente sobre falácias lógicas, o mau raciocínio é generalizado e muitas vezes extremamente eficaz—no sentido em que as pessoas são muitas vezes persuadidas por ele. Na lógica, o padrão da bondade não é a eficácia no sentido da persuasão, mas sim a correção de acordo com as regras lógicas.,por exemplo, considere Hitler. Ele persuadiu uma nação inteira a ir junto com uma variedade de propostas que não eram apenas falsas, mas absolutamente mal. Você não vai se surpreender ao ouvir que se você examiná-lo criticamente, seu raciocínio não passa Reunião lógica. Os argumentos de Hitler eram eficazes, mas não logicamente corretos. Além disso, suas técnicas persuasivas vão além do raciocínio no sentido de apoiar reivindicações com razões. Hitler dependia de ameaças, manipulação emocional, afirmações não fundamentadas, etc. Há muitos truques retóricos que se pode usar para persuadir.,

na lógica, estudamos as regras e técnicas que nos permitem distinguir o raciocínio bom, correto do mau, raciocínio incorreto.

Uma vez que há uma variedade de diferentes tipos de raciocínio e métodos com os quais avaliar cada um destes tipos, além de várias opiniões divergentes sobre o que constitui raciocínio correto, há muitas abordagens para a empresa lógica. Falamos de lógica, mas também de lógica. Uma lógica é apenas um conjunto de regras e técnicas para distinguir o bom raciocínio do mau., Uma lógica deve formular normas precisas para avaliar o raciocínio e desenvolver métodos para aplicar essas normas a casos específicos.

Noções básicas

raciocínio envolve alegações ou afirmações—fazendo-as e apoiando-as com razões, desenhando as suas consequências. Proposições são as coisas que reivindicamos, estado, afirmação.as proposições são os tipos de coisas que podem ser verdadeiras ou falsas. Eles são expressos por sentenças declarativas., Nós usamos tais sentenças para fazer todo tipo de afirmações, desde assuntos de rotina de fato (“a Terra gira em torno do sol”), até grandes teses metafísicas (“a realidade é um absoluto unificado, imutável”), até reivindicações sobre moralidade (“é errado comer carne”).

é importante distinguir sentenças no estado de espírito declarativo, que expressam proposições, de sentenças em outros estados de humor, que não o fazem. Frases interrogativas, por exemplo, fazem perguntas (“está chovendo?”), e sentenças imperativas emitem comandos (“não beba querosene.”)., Não faz sentido perguntar se este tipo de sentenças expressam verdades ou falsidades, para que não expressem proposições.

também distinguimos proposições das sentenças que as expressam, porque uma única proposição pode ser expressa por sentenças diferentes. “It’s raining “e” es regnet ” ambos expressam a proposição de que está chovendo; uma frase faz isso em inglês, a outra em alemão. Além disso,” João ama Maria “e” Maria é amada por João ” ambos expressam a mesma proposição.

a unidade fundamental do raciocínio é o argumento., Na lógica, por “argumento” não estamos falando de um desacordo, uma gritaria de correspondência; em vez disso, temos que definir o termo precisão:

Argumento = um conjunto de proposições, uma das quais, a conclusão, é (deveria ser), apoiado por outros, o local.

Se estamos raciocinando fazendo reivindicações e apoiando-as com razões, então a alegação que está sendo apoiada é a conclusão de um argumento; as razões dadas para apoiá-lo são as premissas do argumento., Se estamos a raciocinar ao extrair uma inferência de um conjunto de afirmações, então a inferência que retiramos é a conclusão de um argumento, e as afirmações a partir das quais ele é extraído são as premissas.

incluímos a cobertura parentética – “suposto ser” – na definição para dar espaço a maus argumentos. Um mau argumento, muito grosso modo, é aquele em que as premissas não apoiam a conclusão; as premissas de um bom argumento apoiam realmente a conclusão.

Análise de argumentos

a seguinte passagem expressa um argumento:

assim faz esta passagem:

novamente, o objetivo final da lógica é avaliar argumentos—para distinguir o bom do mau. Para isso, são necessárias distinções, definições, princípios e técnicas que serão delineadas nos capítulos seguintes. Por agora, vamos nos concentrar na identificação e reconstrução de argumentos.

A primeira tarefa é explicar argumentos-para indicar explicitamente as suas premissas e conclusões., Uma maneira perspicaz de fazer isso é simplesmente listar sentenças declarativas expressando as proposições relevantes, com uma linha separando as premissas da conclusão, assim:

1. Mcdonald’s paga seus trabalhadores salários muito baixos.os animais que fornecem a carne do Mcdonald’s são criados em condições deploráveis.a comida do Mcdonald’s não é saudável.esta é uma explicação da primeira passagem argumentativa acima., Para identificar a conclusão de um argumento, é útil perguntar a si mesmo: “o que essa pessoa está tentando me convencer a acreditar dizendo essas coisas? Qual é o objetivo final desta passagem?”A resposta é bastante clara neste caso. Outra pista sobre o que está acontecendo na passagem é fornecida pela palavra “porque” na terceira frase. Junto com outras palavras, como “Desde” e “para”, indica a presença de uma premissa. Podemos chamar a essas palavras marcadores de premissa. O símbolo “/∴” pode ser lido como estenografia para “Portanto.,”Junto com expressões como “conseqüentemente”, “assim”, “segue-se que” e “o que implica que” “conseqüentemente” é um indicador que a conclusão do argumento está prestes a seguir. Chamamos a essas localizações marcadores de conclusão. Tal marcador não está presente no primeiro argumento, mas vemos um no segundo, que pode ser explicado assim:
   1. o universo é vasto e complexo.o universo apresenta um grau de ordem surpreendente.os planetas orbitam o sol de acordo com leis regulares.as partes mais pequenas dos animais são dispostas precisamente para servir os seus fins.,
   2. tal ordem e complexidade não podem surgir aleatoriamente.portanto, o universo deve ser o produto de um designer de enorme poder e intelecto: Deus.vários pontos de comparação com a nossa primeira explicação são dignos de nota aqui. Em primeiro lugar, como mencionado, fomos alertados da conclusão pela palavra “portanto.”Em segundo lugar, esta passagem necessitava de muito mais paráfrase do que a primeira. A segunda frase é interrogativa, não declarativa, e assim não expressa uma proposição., Uma vez que os argumentos são, por definição, coleções de proposições, devemos nos restringir a sentenças declarativas ao explicá-las. Uma vez que a resposta à pergunta retórica da segunda frase é claramente “sim”, parafraseamos como mostrado. A terceira frase expressa duas proposições, de modo que, em nossa explicação, as separamos; cada uma delas é uma premissa.por isso, às vezes, quando explicamos um argumento, temos de pegar no que está presente na passagem argumentativa e alterá-lo ligeiramente, para que todas as frases que escrevemos expressem as proposições presentes no argumento., Isto é parafraseando. Noutras vezes, temos de fazer ainda mais. Por exemplo, podemos ter que introduzir proposições que não são explicitamente mencionadas dentro da passagem argumentativa, mas são sem dúvida usadas dentro do raciocínio do argumento.

      Há uma palavra grega para passagens argumentativas que deixam certas proposições desamparadas: enthymemes. Aqui está um exemplo:

      não pode haver um Deus Todo-amoroso, porque muitas pessoas inocentes em todo o mundo estão sofrendo.,

      há uma premissa implícita escondida no fundo aqui-algo que não foi dito, mas que precisa ser verdadeiro para o argumento passar. Precisamos de uma afirmação que ligue a premissa à conclusão—que reduza o fosso entre elas. Algo assim: um Deus Todo-amoroso não permitiria que pessoas inocentes sofressem. Ou talvez: o sofrimento generalizado é incompatível com a idéia de uma divindade totalmente amorosa. A premissa aponta para o sofrimento, enquanto a conclusão é sobre Deus; estas proposições ligam essas duas reivindicações., Uma explicação completa da passagem argumentativa faria uma proposição como esta explícita: muitas pessoas inocentes em todo o mundo estão sofrendo.um Deus Todo-amoroso não permitiria que pessoas inocentes sofressem.portanto, não pode haver um Deus Todo-amoroso.esta é a marca dos tipos de premissas tácitas que queremos descobrir: se são falsas, minam o argumento., Muitas vezes, premissas como esta não são atacadas por uma razão: elas são reivindicações controversas por conta própria, exigindo evidências para apoiá-las; então o arguer deixa-as de fora, preferindo não ficar atoladas. Porém, quando os atraímos para fora, podemos forçar uma troca dialética mais robusta, focando o argumento no cerne da questão. Neste caso, uma discussão sobre a compatibilidade da bondade e do mal de Deus no mundo estaria em ordem. Há muito a dizer sobre esse assunto., Filósofos e teólogos desenvolveram argumentos elaborados ao longo dos séculos para defender a ideia de que a bondade de Deus e o sofrimento humano são de fato compatíveis.até agora, a nossa análise de argumentos não foi particularmente profunda. Registámos a importância de identificar a conclusão e de indicar claramente as premissas, mas não analisámos a forma como conjuntos de premissas podem apoiar as suas conclusões. Constatámos apenas que, colectivamente,as premissas apoiam as conclusões., Nós não olhamos como eles fazem isso, que tipos de relacionamentos eles têm um com o outro. Isto requer uma análise mais profunda.muitas vezes, diferentes premissas sustentam uma conclusão—ou outra premissa—individualmente, sem a ajuda de quaisquer outras. Considere este simples argumento:

      ① a invasão do Iraque pela América foi um ato de agressão, não de autodefesa. Além disso, ② não era razoável esperar que os benefícios da guerra superassem os horrores inevitáveis que iria desencadear. Portanto, ③ a guerra do Iraque não foi uma guerra justa.,

      proposições 1 e 2 suportam a conclusão, proposição 3—e eles fazem isso independentemente. Cada um nos dá uma razão para acreditar que a guerra foi injusta, e cada um permanece como uma razão, mesmo se fôssemos supor que o outro não era verdadeiro; esta é a marca de premissas independentes.

      pode ser útil, especialmente quando os argumentos são mais complexos, para desenhar diagramas que retratam as relações entre premissas e conclusão., Nós poderíamos descrever o argumento acima como segue:

      

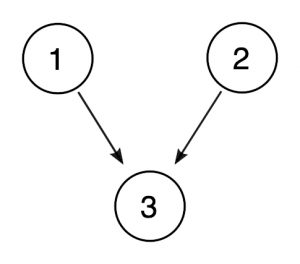
      em tal diagrama, os números circulados representam as proposições e as setas representam a relação de suporte de uma proposição para outra. Uma vez que as proposições 1 e 2 cada suportam 3 independentemente, eles recebem suas próprias flechas.são possíveis outras relações entre as instalações. Por vezes, as premissas apenas fornecem apoio para conclusões indiretamente, dando-nos uma razão para acreditar em alguma outra premissa, que é intermediária entre as duas reivindicações., Considere o seguinte argumento:

      ① poetas são meros “imitadores” cujas obras obscurecem a verdade; portanto, ② eles têm uma influência corrupta sobre as almas dos cidadãos. ③ Poetas devem, portanto, ser banidos da cidade-estado ideal.

      neste exemplo, a proposição 1 fornece suporte para a proposição 2 (a palavra “portanto” é uma pista), enquanto a proposição 2 suporta diretamente a conclusão em 3., Gostaríamos de descrever as relações entre essas proposições, assim:

      

      às Vezes, instalações devem trabalhar juntos para fornecer suporte para uma outra reivindicação, não porque um deles fornece a razão para acreditar que o outro, mas porque não oferece o suporte necessário sobre a sua própria; nós chamamos tais proposições conjuntas local. Considere o seguinte:

      ① se a verdadeira inteligência artificial é possível, então deve-se ser capaz de programar um computador para estar consciente. ② Mas é impossível programar a consciência. Portanto, a verdadeira inteligência artificial é impossível.,

      neste argumento, nem a premissa 1 nem a premissa 2 suportam a conclusão por si só; em vez disso, a segunda premissa, por assim dizer, fornece uma chave que desbloqueia a conclusão da premissa condicional 1. Podemos indicar que tais interdependência diagrama com parênteses, assim:

      

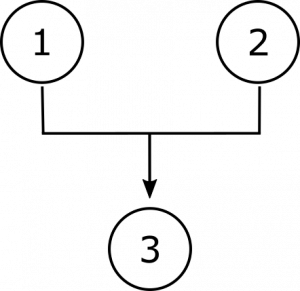
      Diagramação argumentos desta forma, pode ser útil na compreensão de como eles funcionam e informar qualquer tentativa de envolver-se criticamente com eles., Pode-se ver claramente no primeiro argumento que quaisquer considerações apresentadas contra uma das premissas independentes não prejudicarão completamente o apoio à conclusão, uma vez que existe ainda uma outra premissa que lhe fornece algum apoio. No segundo argumento, porém, razões reveladoras contra a segunda premissa cortariam o apoio à conclusão na sua raiz; e tudo o que for contrário à primeira premissa deixará a segunda em necessidade de apoio. E, no terceiro argumento, considerações contrárias a qualquer das premissas comuns prejudicarão o apoio à conclusão., Especialmente quando os argumentos são mais complexos, tais ajudas visuais podem nos ajudar a reconhecer todas as inferências contidas no argumento.

      talvez seja útil concluir considerando um argumento um pouco mais complexo. Consideremos a natureza dos números:

      ① os números são objetos abstratos ou concretos. ② They cannot be concrete objects because ③ they don’t have a location in space and they they don’t interact causally with other objects. Portanto, os números ⑤ são objetos abstratos.,

      a conclusão deste argumento é a última proposição, que os números são objetos abstratos. Note que a primeira premissa nos dá uma escolha entre esta reivindicação e uma alternativa—que eles são concretos. A segunda premissa nega que alternativa, e assim premissas 1 e 2 estão a trabalhar em conjunto para apoiar a conclusão:

      

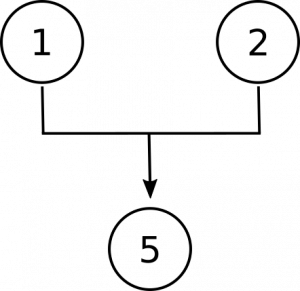
      Agora precisamos fazer o quarto em nosso diagrama para proposições 3 e 4. Eles estão lá para nos dar razões para acreditar que os números não são objetos concretos., Primeiro, ao afirmar que os números não estão localizados no espaço como os objetos concretos estão, e segundo ao afirmar que os números não interagem com outros objetos, como os objetos concretos fazem. Estes são separados, independente de razões para acreditar que eles não são concretos, portanto, vamos acabar com este diagrama:

      

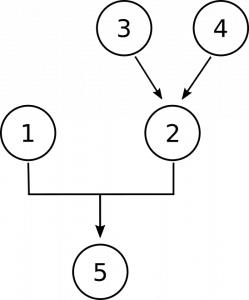
      Lógica e Filosofia

      No coração da lógica empresarial é uma questão filosófica: o Que faz um bom argumento? Ou seja, o que é para um conjunto de reivindicações para fornecer apoio para alguma outra alegação? Ou talvez: quando nos justificamos em tirar inferências?, Para responder a estas questões, os lógicos desenvolveram uma grande variedade de sistemas lógicos, cobrindo diferentes tipos de argumentos e aplicando diferentes princípios e técnicas. Muitas das ferramentas desenvolvidas na lógica podem ser aplicadas além dos limites da filosofia. O matemático provando um teorema, o cientista da computação programando um computador, o linguista modelando a estrutura da linguagem—tudo isso está usando métodos lógicos., Porque a lógica tem uma aplicação tão ampla, e por causa da sofisticação formal/matemática de muitos sistemas lógicos, ela ocupa um lugar único no currículo filosófico. Uma classe na lógica é tipicamente diferente de outras classes de Filosofia em que muito pouco tempo é gasto diretamente engajando-se e tentando responder às “grandes questões”; em vez disso, um muito rapidamente se reduz ao negócio de aprendizagem formalismos lógicos. As questões que a lógica está tentando responder são questões filosóficas importantes, mas as técnicas desenvolvidas para respondê-las são dignas de estudo por si só.,

      isto não significa, no entanto, que devamos pensar na lógica e na filosofia como meramente tangencialmente relacionadas; pelo contrário, elas estão profundamente entrelaçadas. Para todos os sinos e assobios formais apresentados no mais recente sistema lógico High-end, No fundo é parte de um esforço para responder à questão fundamental do que se segue a partir do quê. Além disso, a lógica é útil para o filósofo praticante em pelo menos três outras maneiras.os filósofos tentam responder a perguntas profundas e irritantes sobre a natureza da realidade, o que constitui uma boa vida, como criar uma sociedade justa, e assim por diante., Dão as suas respostas a estas perguntas, e apoiam essas respostas com razões. Então outros filósofos consideram seus argumentos e respondem com elaborações e críticas—argumentos próprios. A filosofia é conduzida e faz progressos através da troca de argumentos. Uma vez que eles são a principal ferramenta de seu comércio, filósofos melhor saber um pouco sobre o que faz para bons argumentos! A lógica, portanto, é essencial para a prática da filosofia.,

      mas a lógica não é apenas uma ferramenta para avaliar argumentos filosóficos; ela alterou o curso da conversa filosófica em curso. À medida que os lógicos desenvolveram sistemas formais para modelar a estrutura de uma gama cada vez mais ampla de práticas discursivas, os filósofos foram capazes de aplicar seus insights diretamente aos problemas filosóficos tradicionais e reconhecer avenidas de investigação anteriormente ocultas. Desde a virada do século XX, especialmente, a proliferação de abordagens novas na lógica provocou uma revolução na prática da filosofia., Não é exagero dizer que grande parte da história da filosofia no século XX constituiu uma tentativa contínua de lidar com novos desenvolvimentos na lógica, e o foco filosófico na linguagem que eles pareciam exigir. Nenhum tópico filosófico – da metafísica à ética à epistemologia e além—foi intocado por esta revolução.finalmente, a lógica em si é a fonte de questões filosóficas fascinantes. A questão básica em seu coração-o que é para uma reivindicação a seguir de outros?,- se espalha em inúmeras direções, proporcionando terreno fértil para a especulação filosófica. Há a lógica, e depois há a filosofia da lógica. A lógica é dita ser “formal”, por exemplo. O que significa? É uma pergunta surpreendentemente difícil de responder. Nossas formulações lógicas mais simples de sentenças condicionais (aquelas que envolvem “se”), levam a paradoxos aparentes. Como resolvê-los? Os nossos formalismos devem ser alterados para melhor captar os significados da linguagem natural dos condicionalismos? Afinal, qual é a relação adequada entre sistemas lógicos e línguas naturais?,

      tradicionalmente, a maioria dos lógicos aceitaram que a lógica deveria ser “bivalente”: toda proposição é verdadeira ou falsa. Mas as línguas naturais contêm termos vagos cujos limites de aplicabilidade nem sempre são claros. Por exemplo,” careca”: para certos assuntos, podemos estar inclinados a dizer que eles estão bem em seu caminho para a calvície completa, mas ainda não completamente lá; por outro lado, estaríamos relutantes em dizer que eles não são-calvos. Há casos intermédios. Para tais casos, poderíamos querer dizer, por exemplo, que a proposição de que Fredo é careca não é verdadeira nem falsa., Alguns lógicos desenvolveram lógicas que não são bivalentes, para lidar com este tipo de fenômeno linguístico. Alguns adicionam um terceiro valor-verdade:” Nem “ou” indeterminado”, por exemplo. Outros introduzem graus infinitos de verdade (isto é chamado de “lógica difusa”). Estas lógicas desviam-se das abordagens tradicionais. Estão, portanto, de algum modo, errados? Ou estão certos e os tradicionalistas errados? Ou será que estamos sequer a fazer uma pergunta sensata quando perguntamos se um determinado sistema lógico está certo ou errado?, Podemos ser chamados de “pluralistas lógicos”, aceitando uma variedade de lógicas incompatíveis, dependendo, por exemplo, se eles são úteis?

      Este tipo de questões estão fora do âmbito deste texto introdutório, é claro. Estão incluídos para dar uma ideia de quão longe se pode levar o estudo da lógica. A tarefa por agora, porém, é começar esse estudo.

      Em primeiro lugar, explique os seguintes argumentos, parafraseando conforme necessário e apenas incluindo premissas tácitas quando explicitamente instruídas para o fazer. Em seguida, Diagrama os argumentos.,os números

      1. , Se existirem, devem ser objetos concretos ou abstratos. Objetos concretos-como planetas e pessoas–são capazes de interagir com outras coisas em relações de causa e efeito. Os números não têm essa capacidade. Portanto, os números são objetos abstratos. abolir a pena de morte! Por quê? É imoral. Numerosos estudos têm mostrado que há preconceito racial em sua aplicação. O aumento dos testes de ADN exonerou dezenas de reclusos no corredor da morte; quem sabe quantas pessoas inocentes foram mortas no passado? A pena de morte também é impraticável., A vingança é contraproducente:” olho por olho deixa o mundo inteiro cego”, como Gandhi disse. Além disso, os custos da litigação dos casos de pena de morte, com os seus intermináveis recursos, são enormes.um sistema económico justo caracterizaria uma distribuição equitativa dos recursos e uma ausência de exploração. O capitalismo é um sistema econômico injusto. Sob o capitalismo, a distribuição típica da riqueza é altamente distorcida em favor dos ricos., E os trabalhadores são explorados: apesar de seu papel essencial na produção de bens para o mercado, a maioria dos lucros da venda desses bens vai para os proprietários das empresas, não seus trabalhadores.a mente e o cérebro não são idênticos. Como é que as coisas podem ser idênticas se têm propriedades diferentes? Há uma propriedade que a mente e o cérebro não compartilham: o cérebro é divisível, mas a mente não. Como todas as coisas materiais, o cérebro pode ser dividido em partes—diferentes metades, regiões, neurônios, etc. Mas a mente é uma unidade. É a minha essência de pensamento, na qual não consigo discernir partes separadas., todos os adultos capazes devem participar na força de trabalho. Quanto mais pessoas trabalham, maior é a riqueza da nação, que beneficia todos economicamente. Além disso, não há substituição para os trabalhadores dignidade encontrar no trabalho. O governo deve, portanto, emitir créditos fiscais para incentivar as pessoas a entrar na força de trabalho.

      1. Os símbolos que precedem a conclusão, “/ \portanto” representam a palavra “portanto.”↵
      2. Esta nem sempre é a razão., Algumas afirmações são deixadas tácitas simplesmente porque todos as aceitam e afirmá-las explicitamente seria uma perda de tempo. Se discutirmos, “os elefantes são mamíferos, e tão de sangue quente”, omitimos a alegação de que todos os mamíferos são de sangue quente por esta razão inocente. ↵
      3. estes argumentos até têm um nome especial: eles são chamados de “teodicias.”↵
      4. uma versão extremamente comprimida das objeções de Platão à poesia no Livro X da República. John MacFarlane, em sua dissertação de Doutorado amplamente lida, gasta mais de 300 páginas nessa questão. Ver: MacFarlane, J. 2000., “O que significa dizer que a lógica é Formal?”University of Pittsburgh. ↵
      5. For a concise explanation, see the Wikipedia entry on paradoxes of material implication. uma versão simplificada de um argumento de Rene Descartes. ↵

      o significado inequívoco das sentenças declarativas.

      sentenças que comunicam que algo é, ou não é, o caso. Por exemplo, ” Bob ganhou os 50m Livres., Sentenças declarativas podem ser contrastadas com aquelas que colocam questões, chamadas sentenças interrogativas, e aquelas que entregam comandos, conhecidas como sentenças imperativas. (Sentenças declarativas também são conhecidas como sentenças indicativas)

      palavras que geralmente indicam o que se segue é uma premissa, por exemplo, “dado que,” “como,” “desde então.”

      Palavras que, geralmente, indicam que o que se segue é uma conclusão, por exemplo “, portanto,” assim,” “, consequentemente.”

      argumentos que deixam certas instalações por preencher.,

      instalações que visam fornecer apoio suficiente por si só para a verdade da conclusão.

      premissas que tentam apoiar diretamente não a conclusão de um argumento, mas outra premissa.

      instalações que apenas apoiam a verdade da conclusão quando combinadas.