LEONARDO FIBONACCI – MATEMÁTICO ITALIANO (ESCREVEU LEBER ÁBACOS)

Leonardo de Pisa (Fibonacci) (c.1170-1250)

O Século 13, o italiano Leonardo de Pisa, mais conhecido pelo apelido de Fibonacci, foi, talvez, o mais talentoso matemático Ocidental da Idade Média. Pouco se sabe de sua vida, exceto que ele era filho de um oficial de costumes e, quando criança, ele viajou pelo norte da África com seu pai, onde aprendeu sobre matemática Árabe., Em seu retorno à Itália, ele ajudou a disseminar esse conhecimento em toda a Europa, dando assim início a um rejuvenescimento na matemática Europeia, que permaneceu em grande parte adormecida durante séculos durante a Idade das Trevas.

Em particular, em 1202, escreveu o influente livro chamado “Liber Ábacos” (“Livro de Cálculo”), em que ele promoveu o uso do sistema Hindu-árabe numeral, descrevendo seus muitos benefícios para os comerciantes e matemáticos tanto sobre o desajeitado sistema de algarismos Romanos, em seguida, em uso na Europa., Apesar de suas vantagens óbvias, a adoção do sistema na Europa foi lenta (isso foi, afinal, durante o tempo das Cruzadas contra o Islã, um tempo em que qualquer coisa árabe foi visto com grande suspeita), e os numerais árabes foram até mesmo banidos na cidade de Florença em 1299, sob o pretexto de que eles eram mais fáceis de falsificar do que os numerais romanos. No entanto, o senso comum finalmente prevaleceu e o novo sistema foi adotado em toda a Europa no século XV, tornando o sistema romano obsoleto., A notação horizontal da barra para frações também foi usada pela primeira vez neste trabalho (embora seguindo a prática árabe de colocar a fração à esquerda do inteiro).

Seqüência de Fibonacci

A descoberta da famosa sequência de Fibonacci

Fibonacci é mais conhecido, porém, para sua introdução na Europa de uma determinada sequência de números, que se tornou conhecido como os Números de Fibonacci ou a Seqüência de Fibonacci., He discovered the sequence – the first recursive number sequence known in Europe-while considering a practical problem in the “Liber Abaci” involving the growth of a hipotetic population of rabbits based on idealized assumptions. Ele observou que, depois de cada geração mensal, o número de pares de coelhos aumentou de 1 a de 2 a de 3 a de 5 a 8, 13, etc, e identificada como a sequência progrediu adicionando os últimos dois termos (em termos matemáticos, Fn = Fn-1 + Fn-2), uma sequência que poderia, em teoria estender indefinidamente.,

A sequência, que tinha, na verdade, foi conhecido matemáticos Indianos desde o Século 6, tem muitas propriedades matemáticas interessantes, e muitas das implicações e relações de sequência não foram descobertos até vários séculos depois de Fibonacci é a morte., Por exemplo, a sequência de regenera-se em algumas formas surpreendentes: a cada terceiro número-F é divisível por 2 (F3 = 2), cada quarto número F é divisível por 3 (F4 = 3), cada quinto número F é divisível por 5 (F5 = 5), a cada sexta número F é divisível por 8 (F6 = 8), cada sétimo F-número é divisível por 13 (F7 = 13), etc., Os números da sequência também foi encontrado para ser onipresente na natureza, entre outras coisas, muitas espécies de plantas com flores têm números de pétalas na Seqüência de Fibonacci; a espiral arranjos de abacaxis ocorrer em 5s e 8s, aqueles de pinecones em 8s e 13s, e as sementes de girassol cabeças, 21s, 34s, 55s ou mais termos na seqüência; etc.,

A Razão de Ouro φ

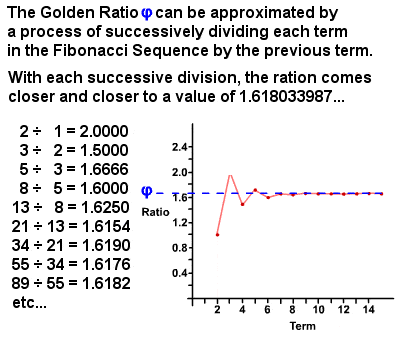
A Razão de Ouro φ pode ser derivada a partir da Sequência de Fibonacci

Na década de 1750, Robert Simson observou que a relação de cada termo da Seqüência de Fibonacci para o termo anterior abordagens, cada vez, com maior precisão, maior a termos, uma proporção de aproximadamente 1 : 1.6180339887 (na verdade é um número irracional igual a (1 + √5)⁄2 que já foi calculado para milhares de casas decimais)., Este valor é referido como a razão dourada, também conhecida como a média dourada, seção dourada, proporção divina, etc, e é geralmente denotado pela letra grega Phi φ (Ou às vezes a Letra capital Phi Φ). Essencialmente, duas quantidades estão na razão dourada se a razão da soma das quantidades para a quantidade maior é igual à razão da quantidade maior para a menor. A razão dourada em si tem muitas propriedades únicas, como 1⁄φ = φ – 1 (0,618…) e φ2 = φ + 1 (2,618…), e há inúmeros exemplos dela a ser encontrada tanto na natureza como no mundo humano.,

Um retângulo com lados na proporção de 1 : φ é conhecido como um Retângulo Dourado, e muitos artistas e arquitetos de toda a história (que remonta ao antigo Egito e da Grécia, mas particularmente popular na arte Renascentista de Leonardo da Vinci e seus contemporâneos) têm proporcionado suas obras, aproximadamente, usando a Razão de Ouro e de Ouro Retângulos, que são amplamente considerados intrinsecamente esteticamente agradável. Um arco conectando pontos opostos de retângulos de Ouro cada vez menores forma uma espiral logarítmica, conhecida como uma espiral dourada., A razão dourada e a espiral dourada também podem ser encontradas em um surpreendente número de casos na natureza, desde Conchas a flores a chifres de animais a corpos humanos a sistemas de tempestade a galáxias completas.,

deve ser lembrado, porém, que a Seqüência de Fibonacci foi, na verdade, apenas uma muito menor elemento em “Liber Ábacos” – de fato, a seqüência recebida apenas de Fibonacci nome em 1877, quando Eduouard Lucas decidiu prestar homenagem a ele, de nomenclatura da série depois dele – e que Fibonacci mesmo não foi responsável pela identificação de quaisquer das interessantes propriedades matemáticas da sequência, a sua relação com a Média de Ouro e de Ouro Retângulos e Espirais, etc.,

Lattice Multiplicação

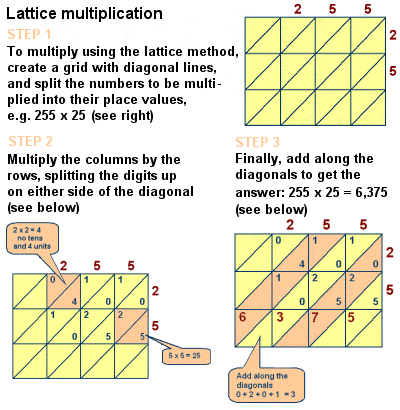
Fibonacci introduziu lattice de multiplicação para a Europa

no Entanto, o livro de influência medieval matemática é inegável, e não também incluir discussões de um número de outros problemas matemáticos, tais como o Chinês Restante Teorema, perfeito números e números primos, fórmulas para a série aritmética e para a praça piramidal números, geométrica Euclidiana provas, e um estudo de equações lineares acopladas ao longo das linhas de Diophantus e Al-Karaji., Ele também descreveu a árvore (ou peneira) método de multiplicação da multiplicação de números grandes, um método originalmente usado por matemáticos Islâmicos como a Al-Khwarizmi – através de um algoritmo equivalente ao longo de multiplicação.

nem era o único livro de “Liber Abaci” Fibonacci, embora fosse o mais importante., O seu “Liber Quadratorum” (“O Livro dos Quadrados”), por exemplo, é um livro sobre álgebra, publicado em 1225, no qual aparece uma declaração do que é agora chamado de Fibonacci de identidade – às vezes, também conhecida como a identidade de Brahmagupta depois de muito antes Indiano matemático, que também chegou às mesmas conclusões que o produto de duas somas de dois quadrados é em si uma soma de dois quadrados de eg (12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,