Resultados da Aprendizagem
- Tornar-se familiarizado com a história da posicional do número de sistemas
- Identificar as bases que têm sido utilizados no número de sistemas historicamente
- Converte números entre bases
- o Uso de dois diferentes métodos para a conversão de números entre bases
Antecedentes
Como você pode imaginar, o desenvolvimento de um sistema de base é um importante passo no sentido de tornar o processo de contagem mais eficiente., Nosso próprio sistema base-dez provavelmente surgiu do fato de que temos 10 dedos (incluindo polegares) em duas mãos. Isto é um desenvolvimento natural. No entanto, outras civilizações tiveram uma variedade de bases que não dez. Por exemplo, os nativos de Queensland usaram um sistema base-dois, contando como segue: “um, dois, dois e um, dois dois, muito.”Algumas tribos modernas sul-americanas têm um sistema base-Cinco contando desta forma:” um, dois, três, quatro, mão, mão e um, mão e dois, ” e assim por diante. Os babilônios usaram um sistema base-60 (sexigesimal)., Neste capítulo, nós terminamos com um exemplo específico de uma civilização que realmente usou um sistema base diferente de 10.
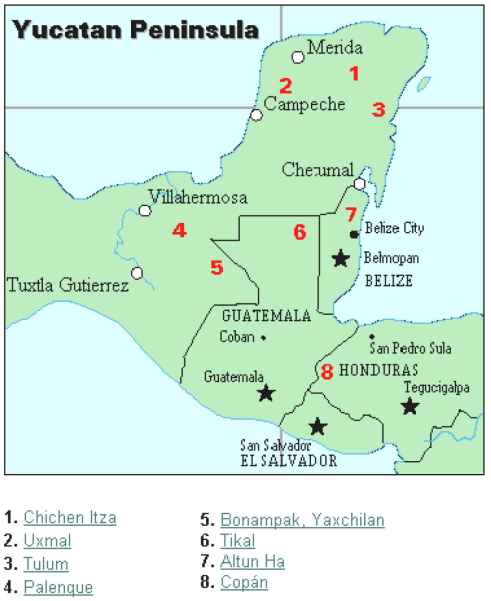 a civilização Maia é geralmente datada de 1500 a. C. a 1700 D. C. A Península de Yucatan (ver Figura 16) no México foi o cenário para o desenvolvimento de uma das civilizações mais avançadas do mundo antigo. Os maias tinham um sistema ritual sofisticado que era supervisionado por uma classe sacerdotal. Esta classe de sacerdotes desenvolveu uma filosofia com o tempo como divino e eterno., O calendário e os cálculos relacionados com ele eram, portanto, muito importantes para a vida ritual da classe sacerdotal e, portanto, do povo Maia. De fato, muito do que sabemos sobre esta cultura vem de seus registros de calendário e dados de Astronomia. Outra importante fonte de informação sobre os maias são os escritos do Padre Diego de Landa, que foi para o México como missionário em 1549.
a civilização Maia é geralmente datada de 1500 a. C. a 1700 D. C. A Península de Yucatan (ver Figura 16) no México foi o cenário para o desenvolvimento de uma das civilizações mais avançadas do mundo antigo. Os maias tinham um sistema ritual sofisticado que era supervisionado por uma classe sacerdotal. Esta classe de sacerdotes desenvolveu uma filosofia com o tempo como divino e eterno., O calendário e os cálculos relacionados com ele eram, portanto, muito importantes para a vida ritual da classe sacerdotal e, portanto, do povo Maia. De fato, muito do que sabemos sobre esta cultura vem de seus registros de calendário e dados de Astronomia. Outra importante fonte de informação sobre os maias são os escritos do Padre Diego de Landa, que foi para o México como missionário em 1549.
 havia dois sistemas numéricos desenvolvidos pelos maias—um para o povo comum e outro para os sacerdotes., Estes dois sistemas não só usavam símbolos diferentes, como também usavam sistemas de base diferentes. Para os sacerdotes, o sistema de números era governado por rituais. Os dias do ano eram considerados deuses, então os símbolos formais para os dias eram cabeças decoradas, como a amostra para a esquerda desde que o calendário básico foi baseado em 360 dias, o sistema de numeração sacerdotal usou um sistema de base mista empregando múltiplos de 20 e 360. Isto torna um sistema confuso, cujos detalhes iremos ignorar.,/td>
havia dois sistemas numéricos desenvolvidos pelos maias—um para o povo comum e outro para os sacerdotes., Estes dois sistemas não só usavam símbolos diferentes, como também usavam sistemas de base diferentes. Para os sacerdotes, o sistema de números era governado por rituais. Os dias do ano eram considerados deuses, então os símbolos formais para os dias eram cabeças decoradas, como a amostra para a esquerda desde que o calendário básico foi baseado em 360 dias, o sistema de numeração sacerdotal usou um sistema de base mista empregando múltiplos de 20 e 360. Isto torna um sistema confuso, cujos detalhes iremos ignorar.,/td>
The Mayan Number System
Instead, we will focus on the numeration system of the “common” people, which used a more consistent base system., Como dissemos anteriormente, Os Maias usaram um sistema base-20, chamado de Sistema “vigesimal”. Tal como o nosso sistema, é posicional, o que significa que a posição de um símbolo numérico indica o seu valor de lugar. Na tabela seguinte você pode ver o valor do lugar em seu formato vertical.
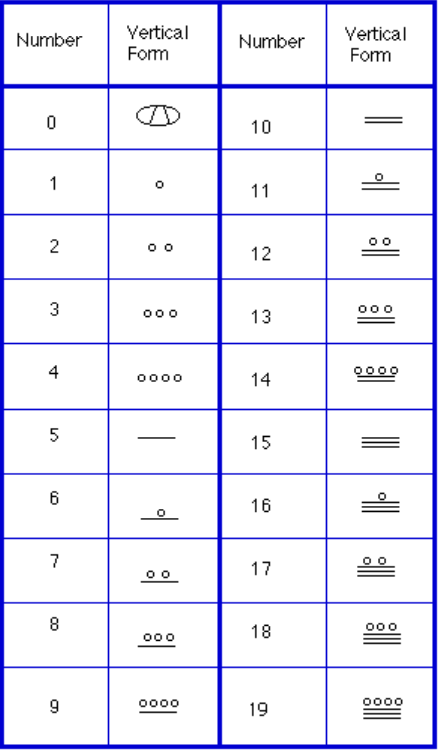
a fim de escrever números para baixo, havia apenas três símbolos necessários neste sistema. Uma barra horizontal representava a quantidade 5, um ponto representava a quantidade 1, e um símbolo especial (pensado para ser uma concha) representava zero., O sistema Maia pode ter sido o primeiro a fazer uso de zero como um substituto/número. Os primeiros 20 números são mostrados na tabela à direita.
Ao contrário do nosso sistema, onde os lugares começam à direita e depois se movem para a esquerda, os sistemas maias colocam os que estão na parte inferior de uma orientação vertical e se movem para cima à medida que o valor do lugar aumenta.
Quando os números são escritos na forma vertical, nunca deve haver mais de quatro pontos em um único lugar. Ao escrever números maias, cada grupo de cinco pontos torna-se uma barra., Além disso, nunca deve haver mais de três barras num único lugar…Quatro Barras seriam convertidas em um ponto no próximo lugar acima. É o mesmo que 10 ser convertido para um 1 no próximo lugar, quando carregamos durante a adição.
exemplo
Qual é o valor deste número, que é mostrado na forma vertical?
Exemplo
o Que é o valor da seguinte Maia número?,
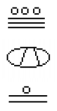
tente
converta o número Maia abaixo para base 10.,

Exemplo
Converter a base 10 de um número 357510 para Maia numerais.
escrevendo números com bases maiores que 10
quando a base de um número é maior que 10, separe cada “dígito” com uma vírgula para tornar clara a separação dos dígitos.
Por exemplo, na base 20, para escrever o número correspondente a 17 × 202 + 6 × 201 + 13 × 200, escreveríamos 17,6,1320.
no vídeo a seguir apresentamos mais exemplos de como escrever números usando Numerais maias, bem como converter numerais escritos em Maias para a forma base 10.,
O próximo vídeo mostra mais exemplos de conversão de números base 10 em números maias.
adicionando números maias
ao adicionar números maias juntos, adotaremos um esquema que os Maias provavelmente não usaram, mas que tornará a vida um pouco mais fácil para nós.
Exemplo
Adicionar, na Maia, com o número 37 e 29 de:

tente adicionar 174 e 78 no Maia, primeiro convertendo-se para números maias e depois trabalhando inteiramente dentro desse sistema. Não adicionar na base-dez (decimal) até ao fim quando verificar o seu trabalho.
Show Solution
no último vídeo mostramos mais exemplos de adição de algarismos maias.,
Neste módulo, temos esboçado brevemente o desenvolvimento de Números e nosso sistema de contagem, com a ênfase na parte “breve”. Existem numerosas fontes de informação e pesquisa que enchem muitos volumes de livros sobre este tema. Infelizmente, não podemos começar a chegar perto de cobrir toda a informação que está lá fora.
apenas arranhámos a superfície da riqueza da investigação e da informação que existe sobre o desenvolvimento de Números e contagem ao longo da história humana., O que é importante notar é que o sistema que utilizamos todos os dias é um produto de milhares de anos de progresso e desenvolvimento. Representa contribuições de muitas civilizações e culturas. Não desce até nós do céu, um presente dos deuses. Não é a criação de um editor de livros. É tão humano como nós, como o resto da matemática. Por trás de cada símbolo, fórmula e Regra há um rosto humano a ser encontrado, ou pelo menos procurado.
além disso, esperamos que você agora tenha uma apreciação básica pelo quão interessantes e diversos sistemas de números podem ficar., Além disso, temos quase a certeza de que vocês também começaram a reconhecer que nós tomamos nosso próprio sistema de números por certo tanto que quando tentamos nos adaptar a outros sistemas ou bases, nós nos encontramos realmente tendo que nos concentrar e pensar sobre o que está acontecendo.







