introdução
neste experimento, você vai observar os comprimentos de onda visíveis da luz produzida por uma descarga elétrica no gás de hélio, usando uma grade de difração. A partir do conhecimento dos valores do comprimento de onda, você será capaz de calibrar com precisão o espaçamento das linhas de grade de difração. Uma vez calibrado, a grade é usada para medir o comprimento de onda da luz produzida pelo hidrogênio atômico. Ao realizar uma curva adequada a estes comprimentos de onda medidos, você pode determinar a constante de Rydberg, uma constante física importante., Esta é uma experiência em que a técnica cuidadosa e medição vai valer a pena: você deve ser capaz de determinar a constante de Rydberg para dentro de um por cento ou melhor. Os gases de hélio e hidrogênio estão contidos em tubos de descarga de baixa pressão que possuem eletrodos metálicos em cada extremidade. Quando uma alta tensão é aplicada através dos dois eletrodos, uma corrente elétrica flui através do gás. Elétrons de alta energia na corrente elétrica colidem com átomos de gás e, no processo, podem transmitir energia interna aos átomos., Estes átomos excitados podem então liberar energia na forma de radiação eletromagnética em comprimentos de onda específicos. Algumas destas radiações electromagnéticas estão dentro do alcance visível.Um professor suíço chamado Johann Balmer (1825 – 1898) estudou os comprimentos de onda da luz visível emitida por átomos de hidrogênio. Ele encontrou uma equação empírica que corresponde com precisão aos valores dos comprimentos de onda observados.,
λ
= R

−
n2

n = 3, 4, 5, 
Aqui, R é a constante de Rydberg 1, o qual foi medido com precisão e têm o valor de R = 10973731.5683 ± 0.0003 m–1. A variável n É qualquer inteiro igual ou superior a 3. A série de comprimentos de onda que resultam de n = 3, 4, 5,…= = ligações externas = = ,1 quântica Moderna teoria da estrutura atômica prevê o valor de R em termos de outras constantes fundamentais: c (velocidade da luz), h (constante de Planck), e (carga do elétron), e m (massa do elétron). O valor experimentalmente medido de R dado acima concorda com a previsão teórica dentro das incertezas combinadas dessas outras constantes fundamentais, dando assim credibilidade à teoria. Este é um bom exemplo de onde a análise de erro é fundamental para nos ajudar a determinar se uma teoria da física realmente descreve a natureza.,Uma grade de difração pode ser usada para observar os comprimentos de onda individuais da luz emitida pelo tubo de descarga. O grating você vai estar usando tem uma linha ou sulco densidade de aproximadamente 300 linhas/mm, assim, o espaçamento de linha d é da ordem de 3 × 10-6 m. Como a luz de comprimento de onda λ do tubo de descarga passa através das grades, ele é difratado através de um ângulo, θ, dado pela grade equação.
aqui M é um inteiro e é chamada a ordem da difração., Para a grade que você estará usando, eles = ± 1 e m = ± 2 ordens serão facilmente observáveis.A disposição experimental vista de cima é mostrada na Figura 1. Você vê a luz do tubo de descarga olhando através da grade de difração. Para os lados esquerdo e direito do tubo você deve ser capaz de ver imagens coloridas do tubo de descarga aparecendo acima e abaixo do medidor stick. A figura 2 mostra a Vista Vista Vista através da grelha.,
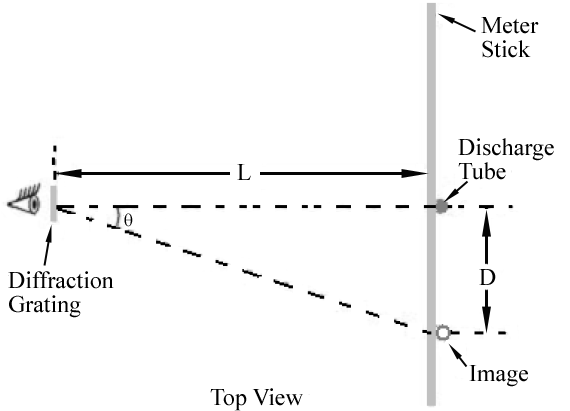
Figura 1
conforme indicado na Figura 1, A imagem de primeira ordem para cada comprimento de onda irá aparecer num ângulo, θ, satisfazendo Eq. (2)
. Assim, diferentes comprimentos de onda aparecerão em diferentes locais ao longo da vara do medidor. O ângulo correspondente a cada comprimento de onda pode ser determinado pela medição D e L.
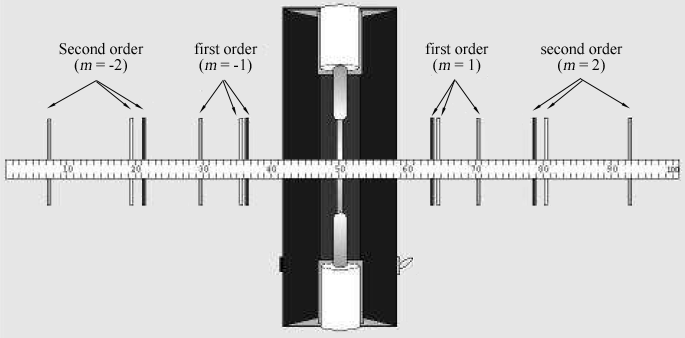
Figura 2: linhas Espectrais visto através da rede de difração de um metro a partir de um tubo de descarga.
Se λ e θ forem conhecidos no Eq., (2)
, então d pode ser determinado. Você vai medir θ Para sete comprimentos de onda conhecidos em hélio. Um ajuste de curva irá então permitir que você determine com precisão o espaçamento de grelha D. na segunda parte do laboratório, você vai usar este valor de d para medir com precisão comprimentos de onda em hidrogênio.
procedimento
Use extrema precaução em torno da fonte de alimentação do tubo de descarga. Produz 5000 volts com corrente suficiente para ser perigosa. Não toque nos eléctrodos de alimentação ou no tubo enquanto o fornecimento Está ligado., Desligue a fonte de alimentação ao mudar os tubos de descarga. Uma vez que a área fica muito quente durante o uso, evite agarrar o meio dos tubos.
Parte 1: espectro de hélio
estabelece o arranjo indicado na Figura 1. Certifique-se que a fonte de alimentação do tubo de descarga está desligada e desligada. Inserir um tubo de gás de hélio nos suportes dos eléctrodos. (Os tubos são frágeis; por favor, manuseie-os com cuidado.) O tubo deve ser direito para cima e para baixo e posicionado perto da marca de 50 cm no medidor stick.,
ligar e ligar a fonte de alimentação. O tubo de descarga deve acender-se imediatamente. Caso contrário, peça ajuda ao instrutor. Um parceiro de laboratório deve olhar através da grade de difração, enquanto o outro parceiro trabalha no lado oposto do medidor stick a fazer leituras.
a pessoa que olha através da grelha de difração deve olhar para a esquerda e para a direita do tubo de descarga para localizar as imagens de difração. Localize a primeira ordem
e a segunda ordem
imagens., Se necessário, rodar a grelha de modo a que as imagens apareçam imediatamente acima e abaixo do medidor stick da mesma forma que o próprio tubo de descarga faz.
A Tabela 1 lista os comprimentos de onda de sete das mais brilhantes linhas visíveis no espectro do hélio na ordem do comprimento de onda mais curto a mais longo. As imagens para cada ordem de difração aparecerão nesta mesma ordem, com o menor comprimento de onda no menor ângulo. Compare as imagens com os comprimentos de onda listados. Olhando através da grade para a direita, localize a posição da primeira imagem ao longo do medidor stick., O parceiro de laboratório que olha através da grade deve instruir o outro parceiro de laboratório para posicionar um pequeno ponteiro (por exemplo, um lápis) ao longo do ponteiro stickuntil o ponteiro está em linha com a imagem sendo medida. O parceiro com o ponteiro, em seguida, lê a posição ao longo do ponteiro. Utilizar uma lâmpada de leitura de baixa potência, se necessário, para ler o contador. Registar a posição XR de cada uma das linhas de hélio na Tabela 1.
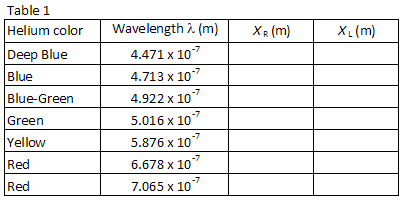
Repita o processo para as sete imagens que aparecem à esquerda do tubo de descarga., Registe a posição XL de cada imagem na Tabela 1.
Parte 2: espectro de hidrogénio
desligar e desligar a fonte de alimentação de descarga e permitir que o tubo de descarga arrefeça durante vários minutos. (Atenção: o tubo será muito quente quando você primeiro desligar o fornecimento.) Remova o tubo de hélio e o substitua pelo tubo de hidrogênio. Colocar a fonte de alimentação de novo com o tubo de hidrogénio na posição de 50 cm ao longo do manípulo do medidor.
três cores facilmente observadas no hidrogénio estão listadas no quadro 2., Combine as cores com as imagens vistas através da grelha de difracção. Registe as posições XR E XL das imagens de primeira ordem na Tabela 2.
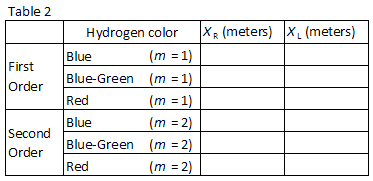
sem perturbar a vareta do medidor ou a grelha de difracção, medir cuidadosamente a distância L Da Figura 1 usando uma medida de fita métrica. Inclua a incerteza no seu valor registado.,
análise
espaçamento de grelha d
para cada comprimento de onda de hélio, calcular a distância média entre o tubo de descarga e as imagens de primeira ordem utilizando a seguinte equação.
XR − XL
além de calcular o
D
L
, θ,
e sin θ para cada comprimento de onda. Regista os teus cálculos na Tabela 3.
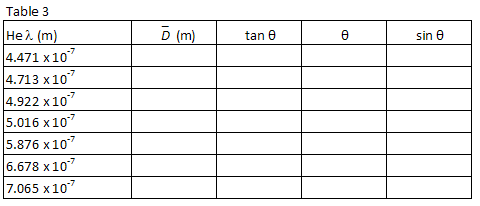
Plot λ vs., sin θ And, using a least squared linear fit, find the slope. A partir do declive do gráfico, encontrar a sua melhor estimativa para a barra de espaçamento, d, em metros e o erro estimado em d.
Constante de Rydberg
Seguindo o mesmo procedimento utilizado na etapa 1 acima, encontrar sin θ para cada um dos comprimentos de onda de hidrogênio você observou e registro na Tabela 4.
usando o valor para o espaçamento de grelha encontrado no Passo 2 acima e a equação de grelha, Eq., (2)
, calcular o comprimento de onda, em metros, das três linhas de hidrogénio que observou e registar na Tabela 4.
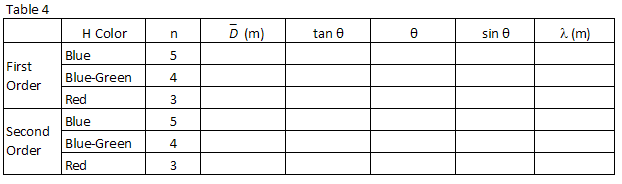
execute um ajuste linear pelo menos quadrado aos seus dados.
Eq. (1)
λ
= R

−
n2

n = 3, 4, 5, 
pode ser reescrito na seguinte forma.,
λ
= R

no2
−
n2

Comparar este formulário para o ajuste da curva de equação para encontrar valores para as constantes R e não. A partir do erro no declive dado pelo ajuste da curva, encontre a incerteza para R.
discussão
resuma os seus resultados para o valor do espaçamento de grelha e a constante de Rydberg (tanto os seus valores como as suas incertezas)., Compare quantitativamente o seu valor para a constante de Rydberg com o valor aceite R = 10973732 m–1.