distribuições
a questão central no coração dos problemas com o delta de Dirac e objetos matemáticos similares é o problema da Diferenciabilidade. Como Dirac afirmou na citação acima, você realmente não tem problemas se você usar sua função δ como uma regra simbólica para como ela age em outras funções; no entanto, ele continua a diferenciar δ em seus cálculos, e é aqui que os problemas realmente começam., Como se pode saber a priori “quando essas operações são permitidas” quando nem sequer se tem uma definição firme dos objetos, ou o que significaria diferenciá-los? Veremos como essas questões levam à derivação de objetos matemáticos novos e rigorosamente definidos.
funções
considere como se determina normalmente a derivada (ou antiderivativa) de uma função. Sob circunstâncias normais, com funções” clássicas”, você tem uma regra bem definida que descreve como uma função mapeia um conjunto de números reais para outro conjunto, digamos f : ℝ→→., Dado isto e as definições da integral ou derivada, pode-se então investigar claramente os valores que esses operadores produzem quando aplicados à função. No caso de δ, Não temos uma definição viável para prosseguir nesta linha. Em vez disso, na prática δ é mais proeminentemente definido pela forma como ele opera em outras funções bem definidas (como em (3)). Esta é a visão chave que leva à teoria moderna das distribuições. Acontece que a maneira correta de tratar matematicamente δ, e uma grande classe de objetos similares, é parar de tentar defini-los como funções., Esta linha de pensamento é bem descrito por Jean Dieudonne em sua revisão de (ver ):
… um começa com uma família de muito “normal” de funções (geralmente com
relativamente ao diferencial de propriedades), que satisfaça determinados (geralmente
integral) de relações, ou em que determinadas operações são possíveis; e
, em seguida, descobre-se que um a priori, maior família de funções satisfaz
as mesmas relações, ou podem ser submetidos a operações semelhantes. Muitas perguntas, então, podem naturalmente ser feitas: esta nova família é realmente diferente da primeira?, Se for, quais são as relações entre as duas famílias, e pode-se dar uma descrição precisa do novo?é apenas na última fase da ” pré-história “que o que pode ser chamado de ponto de vista revolucionário vai surgir, com a ideia de que a” nova família ” pode consistir de objetos que não funções.
os outros objectos aludidos são funções. Você pode pensar em um funcional
como uma função das funções., Como uma função é um mapeamento único de um conjunto de números
para outro, um F funcional pode ser definido como um mapeamento F : C →ℝ,
onde C é algum conjunto de funções. Isto é, um mapa funcional funciona para números reais., Um exemplo simples de um funcional deste tipo é a integral definida:

o que claramente assume uma função f de um conjunto de pessoal com funções integráveis e a mapeia para um número real, o valor da integral, ou de que a área sob a curva de f(x) entre a e b. Este é apenas um exemplo., Pode-se imaginar um número infinito de funcionais, e conjuntos de funcionais; podia até continuar a generalizar e definir mapeamentos de conjuntos de funcionais para números reais. Isso não é aqui nem ali. O importante é que o conceito funcional pode ser usado para definir distribuições.
o conjunto de funções de teste
requeremos mais uma definição para atingir o nosso objectivo. Isto equivale a especificar o conjunto C de funções a partir das quais as distribuições Irão mapear funções para números reais., As funções são frequentemente coletadas em conjuntos que especificam seu grau de continuidade, Diferenciabilidade e continuidade de seus derivados. Dizemos que uma função f está no conjunto C⁰ (escrever f ∈ C⁰) se é contínua sobre toda a linha real no sentido de que o limite em todos os pontos é o mesmo quando tomado da esquerda ou da direita; não é necessariamente diferenciável. Nós dizemos que f ∈ C1 se sua derivada existe e é contínua, ou seja f ‘ ∈ C⁰. Por exemplo, a função g(x) = |x| é contínua mas não diferenciável em x= 0; g é em C⁰, mas não em C1., Podemos generalizar isso e dizer que Cⁿ é o conjunto de funções que têm para funções contínuas suas primeiras derivadas n, onde n é um inteiro.
à medida que n se torna maior, os conjuntos tornam-se num sentido “menor”; você pode sempre encontrar funções (infinitamente muitas!) que estão em Cⁿ mas não em Cⁿ ⁺ 1. Estes “espaços de continuidade” formam, portanto, uma sequência de subconjuntos aninhados, como descrito abaixo.

Perto do final desta sequência infinita de conjuntos de funções que encontramos o conjunto
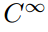
que é, naturalmente, o conjunto de todas as funções que têm um número infinito de derivadas contínuas. Muitas funções bem conhecidas e amigáveis estão nesta última classe (por exemplo, sin(x); cos(x); eˣ; todos os polinômios)., Estas funções são chamadas de “suaves” ou “bem comportadas” porque se pode realizar a operação de diferenciação sobre elas quantas vezes se quiser sem cuidado. Mas embora este conjunto certamente tenha infinitamente muitos membros, eles são raros no sentido de que a maioria das funções não são tão bem comportados.
O conjunto que é adequado para a definição de distribuições é ainda menor do que este. Requer um critério adicional: que as funções tenham suporte compacto. Este termo técnico significa simplesmente que uma função tem valores não-zero dentro de um domínio finito, e é uniformemente zero fora deste., Nós, portanto, utilizar a notação
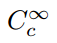
para denotar o conjunto de infinitamente continuamente diferenciáveis funções com suporte compacto, e chamar funções, funções de teste. A fim de definir uma classe de funcionalidades usando este conjunto como um domínio, devemos ter certeza de que existem realmente membros deste conjunto., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

Definição
a Partir deste ponto, a definição de uma distribuição é simples. Uma distribuição é um funcional linear
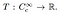
isto é, ele é um mapeamento do conjunto de funções de teste para um número real. Analogous to how a specific function acts on a input number and produces an output, specific distributions are defined by how they transforme test functions into numbers., A distribuição da função de teste φ pode ser escrita como T (φ), ou comumente como〈T, φ〉.
pode-se agora ver porque as distribuições são chamadas funções generalizadas. Para qualquer
clássica função para a qual o integrante

é bem definidas, há uma correspondente distribuição de F tal que 〈F,φ〉dá o valor desta integral., No entanto, existem também distribuições que não correspondem com funções clássicas; distribuições são mais gerais. Como deve ser claro até agora, o exemplo canônico de uma distribuição que não corresponde a uma função clássica é o Dirac δ., Nós, portanto, finalmente, chegar a um totalmente definição rigorosa de δ como a distribuição de tais que

A Generalizada ou “Fraco” Derivado
δ distribuição é apenas um de um número infinito de distribuições que não
correspondem às clássicas funções. Nós podemos obter um pouco mais destes diferenciando δ no sentido de distribuições., Mas como o conceito de distribuição resolve o problema da diferenciação como discutido anteriormente? Só precisamos generalizar o conceito de diferenciação para aplicar às distribuições.
considere uma função f ∈ C1, de modo que seja continuamente diferenciável. O cálculo utilizando a integração por partes, vemos que

O termo em colchetes desaparece desde φ, como uma função de teste, tem suporte compacto., Isso generaliza para uma distribuição de, digamos F”, correspondente à função f’:

Este cálculo generaliza facilmente para distribuições que não correspondem a uma clássica função f., Desta forma, podemos definir a derivada de T’ a T, no sentido de distribuições:

Este é também por vezes referido como o fraco derivados, pois estende-se de derivativos para funções que, normalmente, não ser diferenciável. Isto generaliza-se ainda mais, aos derivados de ordem superior., Podemos definir a enésima derivada de uma distribuição T como T⁽ü⁾, onde o último é a distribuição de tais que

Aqui,
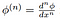
é o clássico derivada da função de teste, qual é assegurada
a existir pela própria definição de funções de teste!, Segue-se que todas as distribuições são infinitamente diferenciáveis (no sentido de distribuições).isto remove inteiramente a luta que Dirac e outros enfrentaram ao diferenciar a função δ. Pelo que definimos aqui, uma derivada de δ simplesmente sifts para o valor de outra função derivada a zero., Formalmente,

Isso fornece um rigoroso modelo matemático para a derivados de δ que apareceu na literatura muito antes de esta teoria veio à existência.
Há uma série de outras operações que se aplicam a funções que foram generalizadas para aplicar a distribuições. Eles podem ser adicionados e subtraídos, convolvidos, e transformados usando a transformação de Laplace e Fourier., No entanto, é impossível definir a multiplicação de distribuições de uma forma que preserve a álgebra que se aplica às funções clássicas (O Teorema da impossibilidade de Schwartz).