os 5 algoritmos de Clustering os cientistas de dados precisam saber

recentemente iniciei uma newsletter educacional focada em livros. Book Dives é uma newsletter bi-semanal onde para cada novo número mergulhamos em um livro não-ficcional. Você aprenderá sobre as lições fundamentais do livro e como aplicá-las na vida real. Pode assinar aqui.

Clustering é uma técnica de aprendizagem de máquina que envolve o agrupamento de pontos de dados. Dado um conjunto de pontos de dados, podemos usar um algoritmo de agrupamento para classificar cada ponto de dados em um grupo específico., Em teoria, os pontos de dados que estão no mesmo grupo devem ter propriedades e/ou características semelhantes, enquanto os pontos de dados em diferentes grupos devem ter propriedades e/ou características muito diferentes. Agrupamento é um método de aprendizagem não supervisionada e é uma técnica comum para a análise de dados estatísticos usados em muitos campos.

na ciência dos dados, podemos usar a análise de agrupamento para obter algumas informações valiosas de nossos dados, vendo em que grupos os pontos de dados caem quando aplicamos um algoritmo de agrupamento., Hoje, vamos olhar para 5 algoritmos de agrupamento populares que os cientistas de dados precisam conhecer e seus prós e contras!

K-Means Clustering

K-Means is probably the most well-known clustering algorithm. É ensinado em muitas aulas introdutórias de ciência de dados e aprendizagem de máquinas. É fácil de entender e implementar em código! Confira o gráfico abaixo para uma ilustração.,

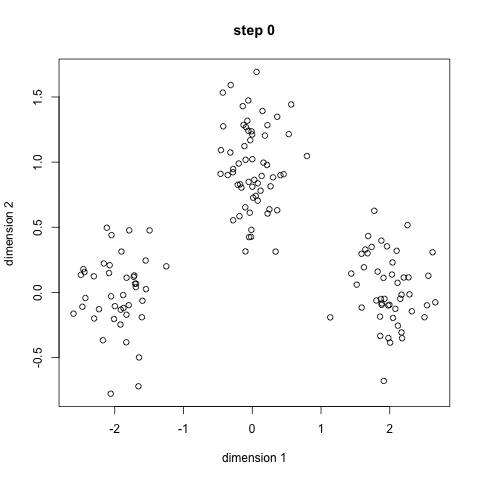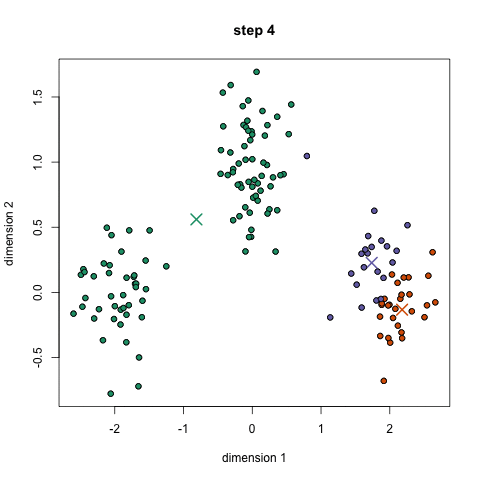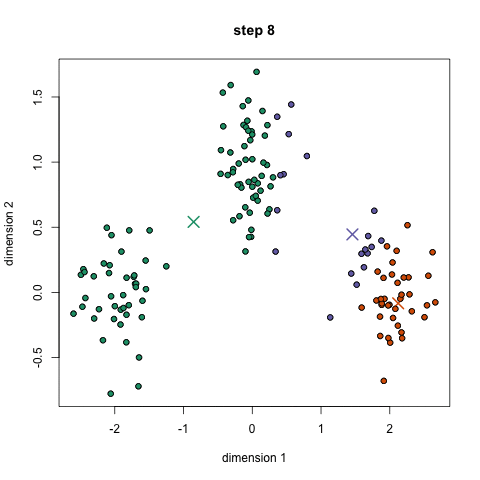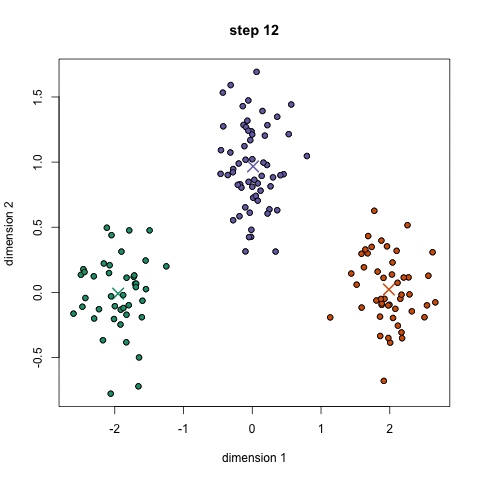
1. Para iniciar, nós primeiro, selecione um número de classes/grupos de usar e aleatoriamente inicializar seus respectivos pontos. Para descobrir o número de classes a usar, é bom dar uma olhada rápida nos dados e tentar identificar qualquer agrupamento distinto. Os pontos centrais são vetores do mesmo comprimento que cada vetor de ponto de dados e são OS” X ” no gráfico acima.,
2. Cada ponto de dados é classificado pela computação da distância entre esse ponto e cada centro de grupo, e então classificando o ponto para estar no grupo cujo centro é mais próximo a ele.com base nestes pontos classificados, recompomos o centro do grupo tomando a média de todos os vetores do grupo.
3. Repita estes passos para um conjunto de iterações ou até que os centros de grupo não mudem muito entre iterações. Você também pode optar por inicializar aleatoriamente os centros de grupo algumas vezes, e, em seguida, selecione a execução que parece que forneceu os melhores resultados.,

k-Means tem a vantagem de ser muito rápido, pois tudo o que estamos fazendo é computar as distâncias entre pontos e centros de grupo; muito poucas computações! Tem, portanto, uma complexidade linear O(n).por outro lado, K-Means tem algumas desvantagens. Em primeiro lugar, você tem que selecionar quantos grupos/classes existem. Isto nem sempre é trivial e idealmente com um algoritmo de agrupamento que gostaríamos que ele descobrisse para nós, porque o objetivo dele é obter alguma visão dos dados., K-means also starts with a random choice of cluster centers and therefore it may yield different clustering results on different runs of the algorithm. Assim, os resultados podem não ser repetíveis e falta de consistência. Outros métodos de cluster são mais consistentes.

K-Medians is another clustering algorithm related to K-Means, except instead of recomputing the group center points using the mean we use the median vector of the group., Este método é menos sensível aos valores anómalos (devido ao uso da mediana), mas é muito mais lento para conjuntos de dados maiores, uma vez que a ordenação é necessária em cada iteração ao calcular o vetor Mediano.

Clustering Mean-Shift

clustering Mean shift é um algoritmo de deslizamento baseado em janelas que tenta encontrar áreas densas de pontos de dados. É um algoritmo baseado em centroides que significa que o objetivo é localizar os pontos centrais de cada grupo/classe, que funciona atualizando candidatos para pontos centrais para ser a média dos pontos dentro da janela de deslizamento., Estas janelas candidatas são então filtradas em uma fase de pós-processamento para eliminar quase duplicados, formando o conjunto final de pontos centrais e seus grupos correspondentes. Confira o gráfico abaixo para uma ilustração.

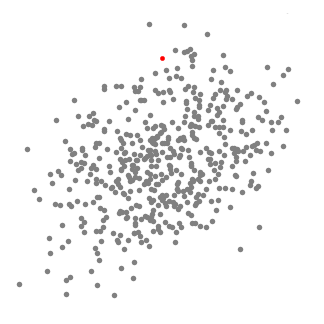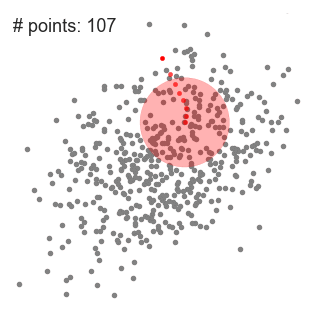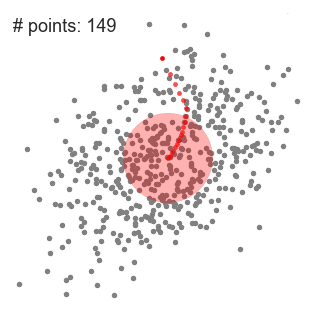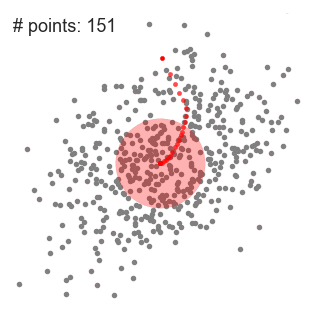
1. Para explicar mean-shift, vamos considerar um conjunto de pontos no espaço bidimensional, como a ilustração acima., Começamos com uma janela de deslizamento circular centrada num ponto C (selecionado aleatoriamente) e com raio r como kernel. Shift médio é um algoritmo de escalada que envolve mudar este kernel iterativamente para uma região de maior densidade em cada passo até a convergência.
2. em cada iteração, a janela de deslizamento é deslocada para regiões de maior densidade, deslocando o ponto central para a média dos pontos dentro da janela (daí o nome). A densidade dentro da janela de deslizamento é proporcional ao número de pontos dentro dela., Naturalmente, ao mudar para a média dos pontos na janela irá gradualmente mover-se para áreas de maior densidade de pontos.
3. continuamos a mudar a janela de deslizamento de acordo com a média até que não haja nenhuma direção na qual uma mudança possa acomodar mais pontos dentro do núcleo. Confira o gráfico acima; continuamos movendo o círculo até que não estamos mais aumentando a densidade (ou seja, o número de pontos na janela).
4. Este processo dos passos 1 a 3 é feito com muitas janelas de deslizamento até que todos os pontos estejam dentro de uma janela., Quando várias janelas de deslizamento sobrepõem a janela que contém a maioria dos pontos é preservada. Os pontos de dados são então agrupados de acordo com a janela de deslizamento em que residem.

Uma ilustração de todo o processo de ponta a ponta com todas as janelas de correr é mostrada abaixo. Cada ponto preto representa o centroide de uma janela deslizante e cada ponto cinzento é um ponto de dados.,

Em contraste com o K-means clustering, não há nenhuma necessidade para selecionar o número de clusters como mean-shift automaticamente descobre isso. É uma grande vantagem. O fato de que os centros de aglomerado convergem para os pontos de densidade máxima também é bastante desejável, pois é bastante intuitivo de entender e se encaixa bem em um sentido naturalmente orientado por dados., A desvantagem é que a seleção do tamanho/raio da janela “r” pode ser não-trivial.

Clustering espacial baseado em densidade de aplicações com ruído (DBSCAN)

DBSCAN é um algoritmo de cluster baseado em densidade semelhante ao deslocamento médio, mas com algumas vantagens notáveis. Confira outro gráfico chique abaixo e vamos começar!,

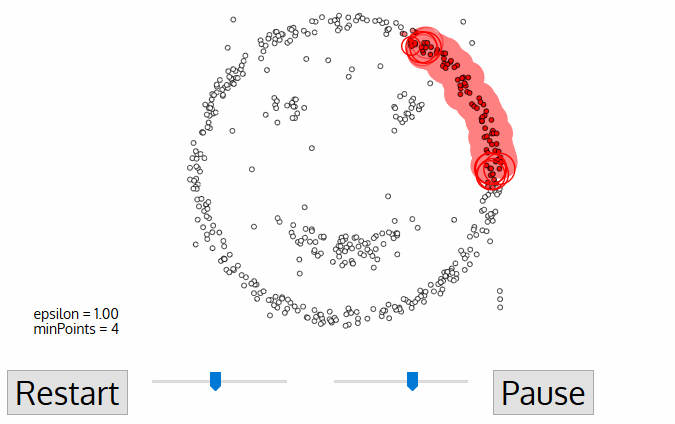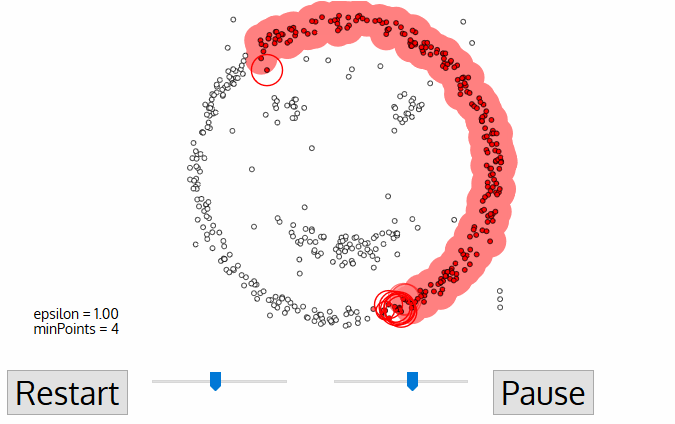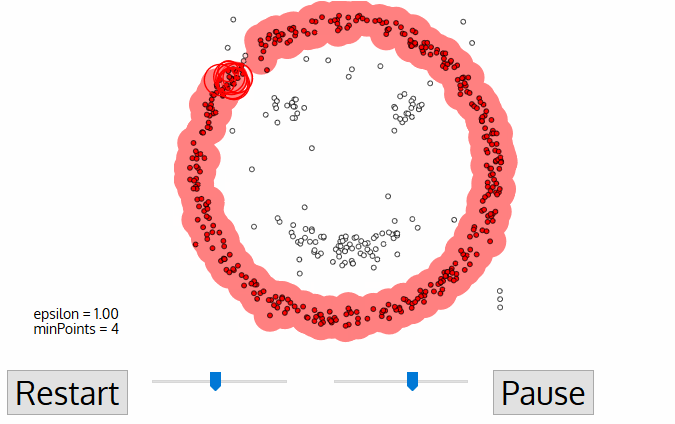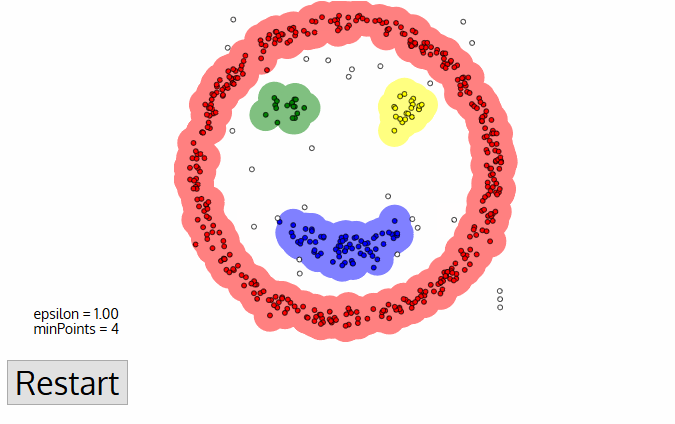
1. DBSCAN começa com uma partida arbitrário ponto de dados que não tenha sido visitado. A vizinhança deste ponto é extraída usando uma distância épsilon ε (todos os pontos que estão dentro da distância ε são pontos de vizinhança).,
2. Se houver um número suficiente de pontos (de acordo com minPoints) dentro desta vizinhança, então o processo de agrupamento começa e o ponto de dados atual se torna o primeiro ponto no novo aglomerado. Caso contrário, o ponto será rotulado como ruído (mais tarde este ponto ruidoso pode se tornar a parte do aglomerado). Em ambos os casos, esse ponto é marcado como”visitado”.
3. para este primeiro ponto no novo aglomerado, os pontos dentro de sua vizinhança ε distância também se tornam parte do mesmo aglomerado., Este procedimento de fazer todos os pontos no bairro ε pertencem ao mesmo cluster é então repetido para todos os novos pontos que foram apenas adicionados ao grupo cluster.
4. Este processo das etapas 2 e 3 é repetido até que todos os pontos do aglomerado sejam determinados, ou seja, todos os pontos dentro da vizinhança ε do aglomerado foram visitados e rotulados.uma vez terminado o cluster atual, um novo ponto não visitado é recuperado e processado, levando à descoberta de outro cluster ou ruído. Este processo se repete até que todos os pontos sejam marcados como visitados., Uma vez que, no final, todos os pontos foram visitados, cada ponto terá sido marcado como pertencente a um aglomerado ou como sendo ruído.

DBSCAN poses some great advantages over other clustering algorithms. Em primeiro lugar, não exige um número pe-set de clusters. Ele também identifica os anómalos como ruídos, Ao contrário do deslocamento médio que simplesmente os joga em um aglomerado, mesmo que o ponto de dados seja muito diferente. Além disso, pode encontrar conjuntos arbitrariamente dimensionados e arbitrariamente moldados bastante bem.,

A principal desvantagem do DBSCAN é que ele não funciona bem como outros quando os clusters são de densidade variável. Isto é porque a definição do limiar de distância ε e minPoints para identificar os pontos da vizinhança vai variar de aglomerado para Aglomerado quando a densidade varia. Esta desvantagem também ocorre com dados muito dimensionais, uma vez que novamente o limiar de distância ε torna-se desafiador para estimar.,

maximização de expectativa (EM) agrupando usando modelos de mistura Gaussianos (GMM)

uma das principais desvantagens do K-Means é o seu uso ingênuo do valor médio para o centro do aglomerado. Podemos ver porque esta não é a melhor maneira de fazer as coisas olhando para a imagem abaixo. No lado esquerdo, parece óbvio para o olho humano que existem dois aglomerados circulares com um raio diferente centrados no mesmo meio. K-Means não pode lidar com isso porque os valores médios dos aglomerados são muito próximos., K-Means also fails in cases where the clusters are not circular, again as a result of using the mean as cluster center.

Gaussian Mixture Models (Mgm) nos dão mais flexibilidade do que o K-means. Com MGM assumimos que os pontos de dados são distribuídos Gaussianos; esta é uma suposição menos restritiva do que dizer que eles são circulares usando a média., Dessa forma, temos dois parâmetros para descrever a forma dos aglomerados: a média e o desvio padrão! Tomando um exemplo em duas dimensões, isto significa que os aglomerados podem ter qualquer tipo de forma elíptica (uma vez que temos um desvio padrão em ambas as direções x e y). Assim, cada distribuição gaussiana é atribuída a um único conjunto.

para encontrar os parâmetros do Gaussiano para cada conjunto (por exemplo, o desvio médio e padrão), vamos usar um algoritmo de otimização chamado maximização de expectativa (em)., Dê uma olhada no gráfico abaixo como uma ilustração dos Gaussianos sendo ajustados aos aglomerados. Então podemos prosseguir com o processo de Clustering de maximização de expectativa usando MGM.

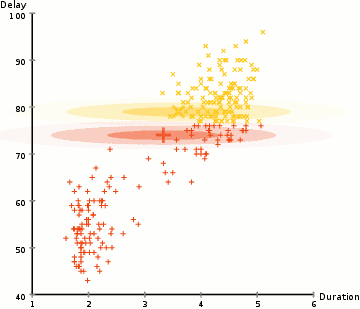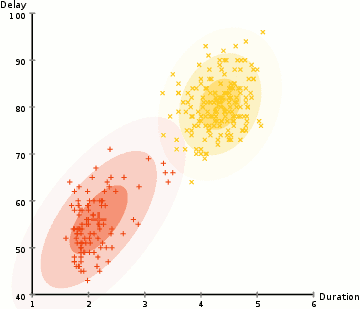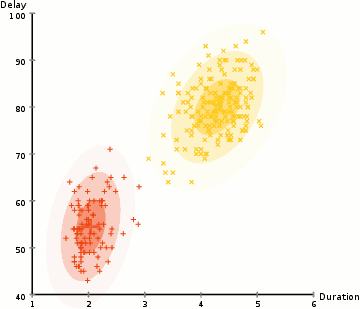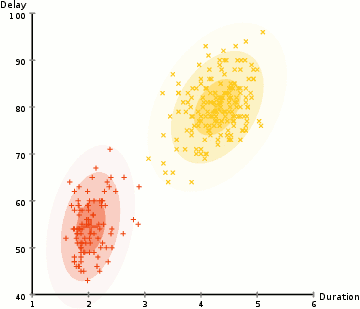
1. Vamos começar selecionando o número de clusters (K-Means faz) e aleatoriamente inicializar a distribuição Gaussiana parâmetros para cada cluster., Pode-se tentar fornecer uma boa estimativa para os parâmetros iniciais, dando uma rápida olhada nos dados também. Apesar de notar, como pode ser visto no gráfico acima, isso não é 100% necessário como os Gaussianos começam o nosso como muito pobres, mas são rapidamente otimizados.
2. dadas estas distribuições Gaussianas para cada aglomerado, calcule a probabilidade de cada ponto de dados pertencer a um determinado aglomerado. Quanto mais perto um ponto está do centro de Gaussian, mais provável ele pertence a esse aglomerado., Isto deve fazer sentido intuitivo já que com uma distribuição gaussiana estamos assumindo que a maioria dos dados está mais perto do centro do aglomerado.
3. Com base nestas probabilidades, computamos um novo conjunto de parâmetros para as distribuições Gaussianas de tal forma que maximizamos as probabilidades de pontos de dados dentro dos aglomerados. Calculamos estes novos parâmetros usando uma soma ponderada das posições dos pontos de dados, onde os pesos são as probabilidades do ponto de dados pertencente a esse conjunto particular., Para explicar isso visualmente, podemos dar uma olhada no gráfico acima, em particular o aglomerado amarelo como um exemplo. A distribuição começa aleatoriamente na primeira iteração, mas podemos ver que a maioria dos pontos amarelos estão à direita da distribuição. Quando calculamos uma soma ponderada pelas probabilidades, mesmo que haja alguns pontos perto do centro, a maioria deles estão à direita. Assim, naturalmente, a média da distribuição é deslocada mais perto daqueles conjuntos de pontos. Também podemos ver que a maioria dos pontos são “cima-direita para baixo-esquerda”., Portanto, o desvio padrão muda para criar uma elipse que é mais ajustada a estes pontos, para maximizar a soma ponderada pelas probabilidades.
4. os passos 2 e 3 são repetidos iterativamente até a convergência, onde as distribuições não mudam muito de iteração para iteração.

Existem 2 vantagens fundamentais para a utilização de MGM. Em primeiro lugar, os MGM são muito mais flexíveis em termos de covariância de aglomerados do que K-Means; devido ao parâmetro de desvio padrão, os aglomerados podem assumir qualquer forma de elipse, em vez de serem restringidos a círculos., K-Means é na verdade um caso especial de GMM em que a covariância de cada conjunto ao longo de todas as dimensões se aproxima de 0. Em segundo lugar, uma vez que os MGM usam probabilidades, eles podem ter múltiplos clusters por ponto de dados. Então, se um ponto de dados está no meio de dois aglomerados sobrepostos, podemos simplesmente definir sua classe dizendo que pertence X-por cento à classe 1 e Y-por cento à classe 2. Os MGM apoiam a associação mista.

a aglomeração hierárquica dos algoritmos de agrupamento hierárquicos

os algoritmos de agrupamento hierárquicos são classificados em 2 categorias: de cima para baixo ou de baixo para cima., Algoritmos Bottom-up tratam cada ponto de dados como um único aglomerado no início e, em seguida, sucessivamente juntar (ou aglomerar) pares de aglomerados até que todos os aglomerados foram fundidos em um único aglomerado que contém todos os pontos de dados. O agrupamento hierárquico ascendente é, portanto, chamado agrupamento aglomerativo hierárquico ou HAC. Esta hierarquia de aglomerados é representada como uma árvore (ou dendrograma). A raiz da árvore é o aglomerado único que reúne todas as amostras, sendo as folhas os aglomerados com apenas uma amostra., Confira o gráfico abaixo uma ilustração antes de passar para o algoritmo de passos

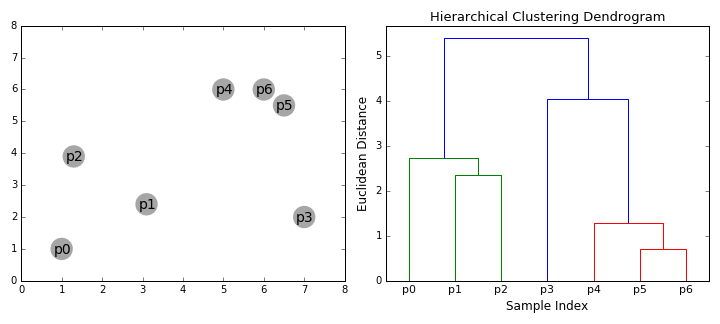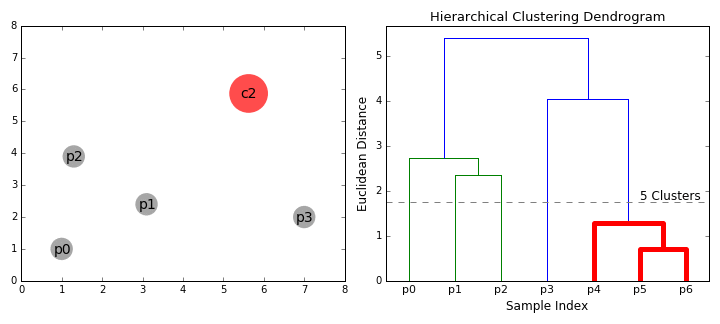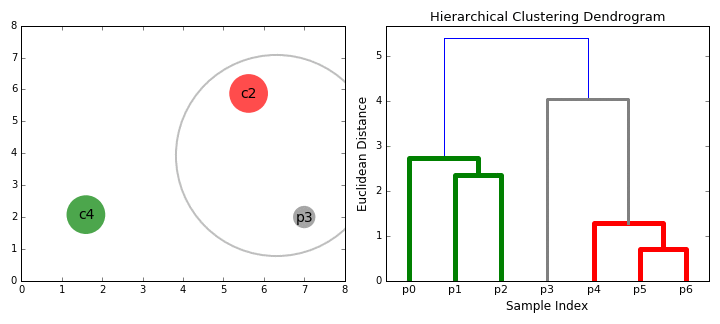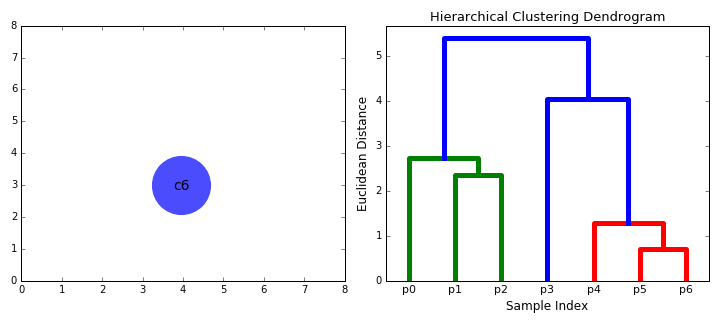
1. Vamos começar por tratar cada ponto de dados como um único cluster i.e se existem X pontos de dados em nosso conjunto de dados, em seguida, temos X clusters. Nós então selecionamos uma métrica de distância que mede a distância entre dois aglomerados., Como exemplo, vamos usar uma ligação média que define a distância entre dois aglomerados para ser a distância média entre pontos de dados no primeiro aglomerado e pontos de dados no segundo aglomerado.em cada iteração, combinamos dois grupos em um. Os dois grupos a serem combinados são selecionados como aqueles com a menor ligação média. Ou seja, de acordo com a nossa métrica de distância selecionada, estes dois aglomerados têm a menor distância entre si e, portanto, são os mais semelhantes e devem ser combinados.
2. Passo 2 é repetido até chegarmos à raiz da árvore I.,e só temos um conjunto que contém todos os pontos de dados. Desta forma, podemos selecionar quantos clusters queremos no final, simplesmente escolhendo quando parar de combinar os clusters I. e quando paramos de construir a árvore!

clustering hierárquico não requer que especificemos o número de clusters e podemos até mesmo selecionar qual o número de clusters mais bonito, uma vez que estamos construindo uma árvore. Além disso, o algoritmo não é sensível à escolha da métrica de distância; todos eles tendem a trabalhar igualmente bem, enquanto que com outros algoritmos de clustering, a escolha da métrica de distância é crítica., Um caso particularmente bom de uso de métodos de agrupamento hierárquicos é quando os dados subjacentes têm uma estrutura hierárquica e você quer recuperar a hierarquia; outros algoritmos de agrupamento não podem fazer isso. Estas vantagens de agrupamento hierárquico vêm ao custo de menor eficiência, uma vez que tem uma complexidade Temporal de O(n3), ao contrário da complexidade linear de K-Means e GMM.