quando uma fração “normal” contém frações no numerador ou denominador ou em ambos, então consideramos que é uma fração complexa. Este tipo de fração também é conhecido como uma fração composta.
Existem dois métodos usados para simplificar este tipo de fração.
Método 1
passos-Chave:
- Criar uma única fração em que o numerador e o denominador.,
- aplica a regra de divisão das fracções multiplicando o numerador pelo recíproco ou inverso do denominador.
- Simplifique, se necessário.
Método 2
passos-Chave:
- Encontrar o Mínimo Denominador Comum (mdc) de todos os denominadores no complexo de frações.
- multiplique este LCD para o numerador e denominador da fracção complexa.Simplifique, se necessário.,
Depois de passar mais alguns exemplos, você deve perceber que o Método 2 é muito melhor do que o Método 1, porque quase sempre ele leva menos etapas para chegar à resposta final.
exemplos de como simplificar frações complexas
exemplo 1: simplificar a fração complexa abaixo.
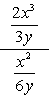
- Usando o Método 1
Tanto o numerador e o denominador do complexo fração já estão expressos como frações individuais. Isto é óptimo!,

O próximo passo a fazer é aplicar a regra de divisão multiplicando-se o numerador pelo recíproco do denominador. Termine cancelando fatores comuns para obter a resposta final.
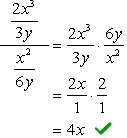
- Usando o Método 2
Encontre LCD de todo o problema, isto é, o LCD da parte superior e inferior de denominadores.,

Desde que o LCD do 3y e 6y é apenas \textbf{6y}, vamos agora multiplicar o complexo numerador e o denominador por este LCD. Depois disso, podemos esperar que o problema seja reduzido a uma única fracção que possa ser simplificada como de costume.
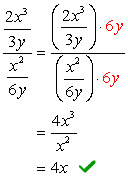
Exemplo 2: Simplificar a complexa fração abaixo.,
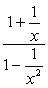
- Usando o Método 1
neste método, queremos criar uma única fração, tanto no numerador e denominador. Obviamente, este problema exigiria que o fizéssemos primeiro antes de realizarmos a divisão.
adicione as fracções no numerador e subtraia as do denominador.,
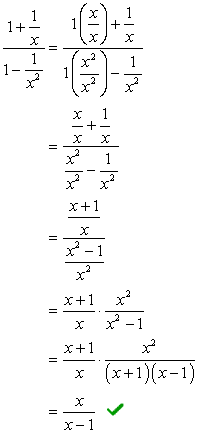
- Usando o Método 2
Olhando para os denominadores \large{x} e \large{x^2}, o seu LCD deve ser \large{x^2} Multiplicar a parte superior e inferior por este LCD.
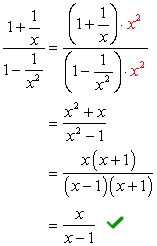
Exemplo 3: Simplificar a complexa fração abaixo.,
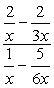
- Usando o Método 1
Criar única frações em que o numerador e o denominador, então siga pela divisão de frações.
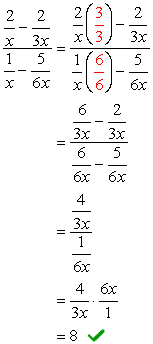
- Usando o Método 2
A geral LCD dos denominadores é \color{red}6x. Use isso para multiplicar através da parte superior e inferior expressões.,
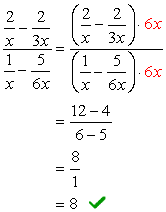
Exemplo 4: Simplifique o complexo fração abaixo.
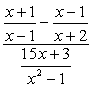
Para este problema, vamos utilizar o Método 1 apenas.
O problema requer que você aplique o método da folha (multiplicação de dois binômios) e uma fatoração simples do trinômio. Pode parecer um pouco intimidante no início; no entanto, se prestar atenção aos detalhes, garanto-lhe que não é assim tão mau.,
Se você observar, o denominador complexo já está na forma que queremos – tendo um símbolo fraccional. Isto significa que temos de trabalhar um pouco no numerador complexo. Nosso próximo passo seria transformar o numerador complexo em uma fração simples ou simples.
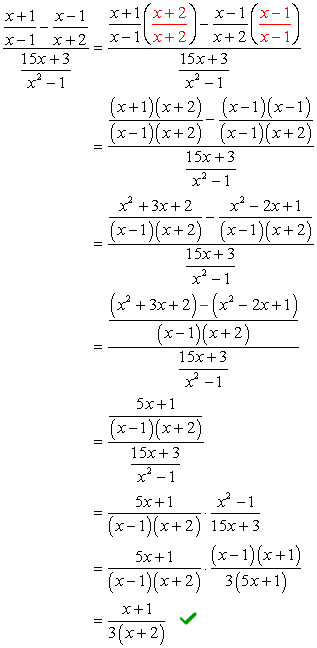
Exemplo 5: Simplificar a complexa fração abaixo.
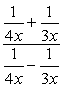
Para este problema, vamos usar o Método 2, apenas.,
Observe que o LCD de todos os denominadores é apenas \color{red}12x. Use isto como o multiplicador comum para as expressões de topo e de baixo.
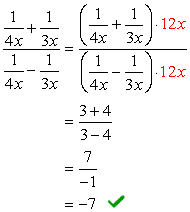
Prática com Planilhas
Você também pode estar interessado em:
Multiplicação de Complexos Frações
Dividir Números Complexos