cei 5 algoritmi de grupare oamenii de știință de date trebuie să știe

am început recent un buletin informativ educațional axat pe carte. Book Dives este un buletin informativ bi-săptămânal în care pentru fiecare număr nou ne scufundăm într-o carte non-ficțiune. Veți învăța despre lecțiile de bază ale cărții și cum să le aplicați în viața reală. Vă puteți abona aici.

Clustering este o tehnică de învățare automată care implică gruparea punctelor de date. Având în vedere un set de puncte de date, putem folosi un algoritm de grupare pentru a clasifica fiecare punct de date într-un anumit grup., În teorie, punctele de date care se află în același grup ar trebui să aibă proprietăți și/sau caracteristici similare, în timp ce punctele de date din diferite grupuri ar trebui să aibă proprietăți și/sau caracteristici foarte diferite. Clustering este o metodă de învățare nesupravegheată și este o tehnică comună pentru analiza datelor statistice utilizate în multe domenii.

în știința datelor, putem folosi analiza grupării pentru a obține informații valoroase din datele noastre, văzând în ce grupuri se încadrează punctele de date atunci când aplicăm un algoritm de grupare., Astăzi, vom analiza 5 algoritmi populari de grupare pe care oamenii de știință de date trebuie să le cunoască și avantajele și dezavantajele lor!

K-înseamnă gruparea

K-înseamnă este probabil cel mai cunoscut algoritm de grupare. Este predată într-o mulțime de cursuri introductive de știință a datelor și de învățare automată. Este ușor de înțeles și implementat în cod! Consultați graficul de mai jos pentru o ilustrație.,

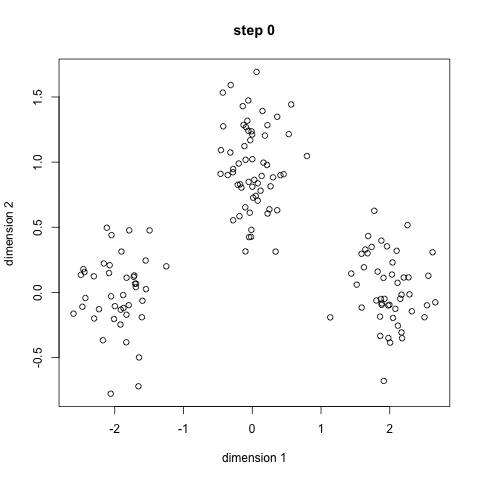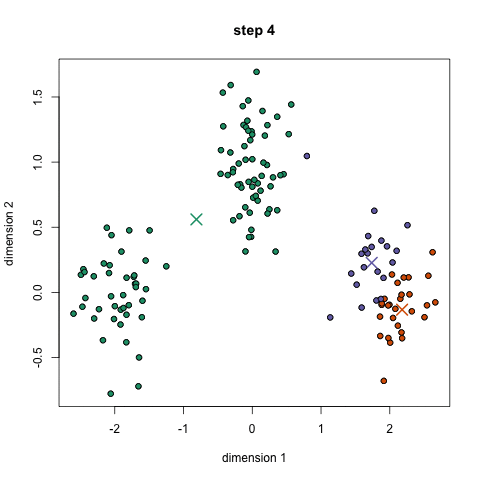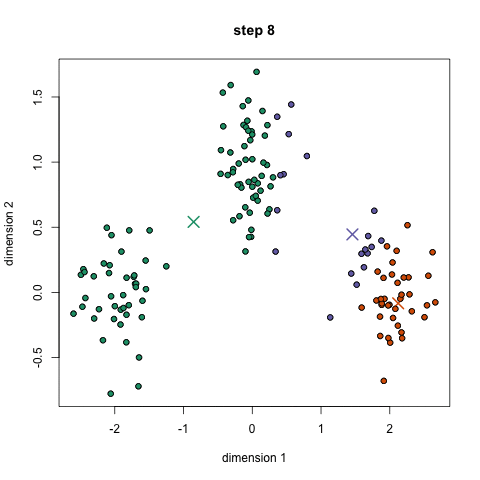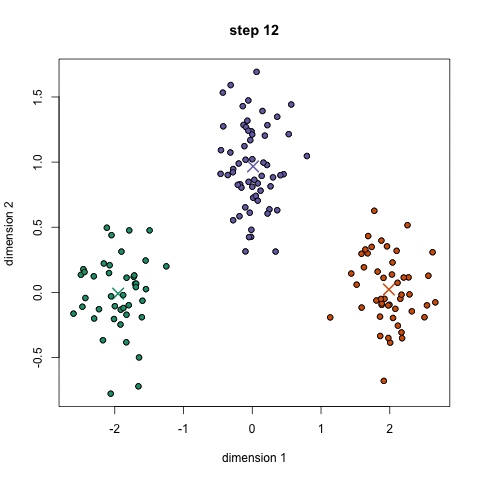
1. Pentru a începe, am selectați mai întâi un număr de clase/grupe pentru a utiliza și la întâmplare inițializa lor respective centru de puncte. Pentru a afla numărul de clase de utilizat, este bine să aruncați o privire rapidă asupra datelor și să încercați să identificați orice grupări distincte. Punctele centrale sunt vectori de aceeași lungime ca fiecare vector de punct de date și sunt „X” în graficul de mai sus.,
2. fiecare punct de date este clasificat calculând distanța dintre acel punct și fiecare centru de grup și apoi clasificând punctul care trebuie să fie în grupul al cărui centru este cel mai apropiat de acesta.
3. Pe baza acestor puncte clasificate, recalculăm centrul grupului luând media tuturor vectorilor din grup.
4. repetați acești pași pentru un anumit număr de iterații sau până când centrele de grup nu se schimbă prea mult între iterații. De asemenea, puteți opta pentru inițializarea aleatorie a centrelor de grup de câteva ori, apoi selectați rularea care pare că a oferit cele mai bune rezultate.,

K-Means are avantajul că este destul de rapid, deoarece tot ce facem cu adevărat este să calculăm distanțele dintre puncte și centrele de grup; foarte puține calcule! Ea are astfel o complexitate liniară O (n).pe de altă parte, K-Means are câteva dezavantaje. În primul rând, trebuie să selectați câte grupuri/clase există. Acest lucru nu este întotdeauna banal și, în mod ideal, cu un algoritm de grupare, am dori să ne dăm seama de acestea pentru că scopul este să obținem o perspectivă din date., K-means începe, de asemenea, cu o alegere aleatorie a centrelor de cluster și, prin urmare, poate da rezultate diferite de clustering pe diferite runde ale algoritmului. Astfel, rezultatele pot să nu fie repetabile și să nu aibă consistență. Alte metode de cluster sunt mai consistente.

K-Medians este un alt algoritm de grupare legat de K-înseamnă, cu excepția cazului în loc de a recompune punctele centrale de grup folosind media folosim vectorul median al grupului., Această metodă este mai puțin sensibilă la valorile aberante (din cauza utilizării medianei), dar este mult mai lentă pentru seturile de date mai mari, deoarece sortarea este necesară pentru fiecare iterație atunci când se calculează vectorul Median.

mean-Shift Clustering

mean shift clustering este un algoritm bazat pe ferestre glisante care încearcă să găsească zone dense de puncte de date. Este un algoritm bazat pe centroid, ceea ce înseamnă că obiectivul este de a localiza punctele centrale ale fiecărui grup/clasă, care funcționează prin actualizarea candidaților pentru punctele centrale pentru a fi media punctelor din fereastra glisantă., Aceste ferestre candidate sunt apoi filtrate într-o etapă post-procesare pentru a elimina duplicatele apropiate, formând setul final de puncte centrale și grupurile lor corespunzătoare. Consultați graficul de mai jos pentru o ilustrație.

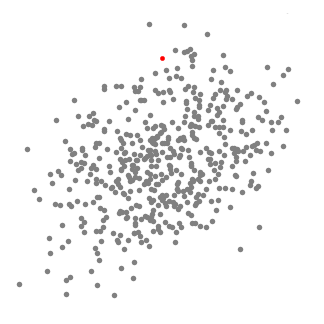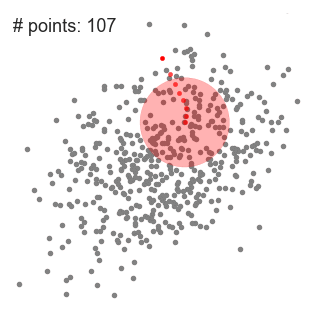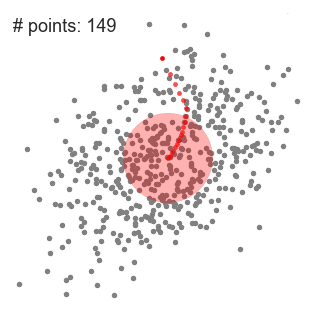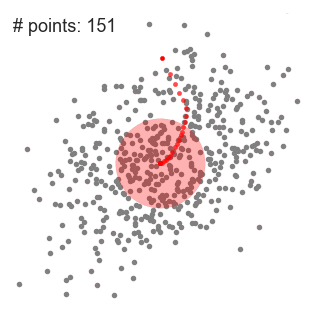
1. Pentru a explica înseamnă schimbare, vom lua în considerare un set de puncte în spațiul bidimensional ca ilustrația de mai sus., Începem cu o fereastră glisantă circulară centrată într-un punct C (selectat aleatoriu) și având raza r ca kernel. Shift medie este un algoritm deal-alpinism, care implică trecerea acest kernel iterativ la o regiune de densitate mai mare pe fiecare pas până la convergență.
2. la fiecare iterație, fereastra glisantă este deplasată spre regiuni cu densitate mai mare prin deplasarea punctului central la media punctelor din fereastră (de unde și numele). Densitatea din fereastra glisantă este proporțională cu numărul de puncte din interiorul acesteia., În mod natural, prin trecerea la media punctelor din fereastră se va muta treptat spre zone cu densitate mai mare a punctelor.
3. continuăm deplasarea ferestrei glisante în funcție de medie până când nu există nicio direcție în care o schimbare poate găzdui mai multe puncte în interiorul kernelului. Verificați graficul de mai sus; continuăm să mișcăm cercul până când nu mai creștem densitatea (adică numărul de puncte din fereastră).
4. acest proces de pași 1 la 3 se face cu multe ferestre glisante până când toate punctele se află într-o fereastră., Atunci când mai multe ferestre glisante se suprapun fereastra care conține cele mai multe puncte este păstrată. Punctele de date sunt apoi grupate în funcție de fereastra glisantă în care locuiesc.

o ilustrare a întregului proces de la capăt la capăt cu toate ferestrele glisante este prezentată mai jos. Fiecare punct negru reprezintă centroidul unei ferestre glisante și fiecare punct gri este un punct de date.,

În contrast cu K-means clustering, nu este nevoie pentru a selecta numărul de clustere ca-shift descoperă în mod automat acest lucru. Acesta este un avantaj masiv. Faptul că centrele de cluster converg spre punctele de densitate maximă este, de asemenea, destul de de dorit, deoarece este destul de intuitiv de înțeles și se potrivește bine într-un sens natural bazat pe date., Dezavantajul este că selectarea dimensiunii/razei ferestrei ” r ” poate fi non-trivială.

Densității Spațiale Gruparea de Aplicații cu Zgomot (DBSCAN)

DBSCAN este o densitate bazate pe cluster algoritm similar mean-shift, dar cu câteva avantaje notabile. Check out un alt grafic fantezie de mai jos și să începem!,

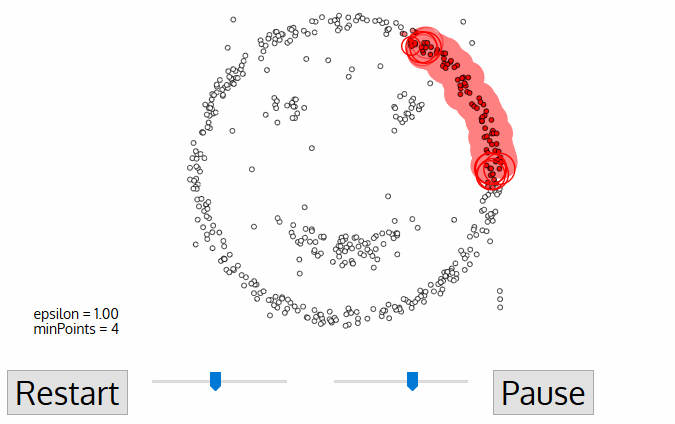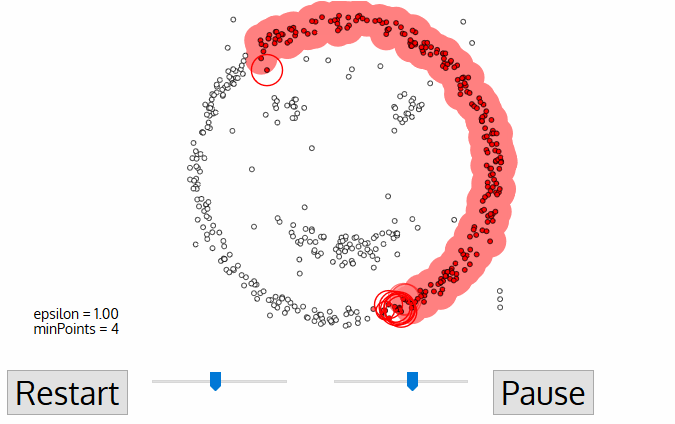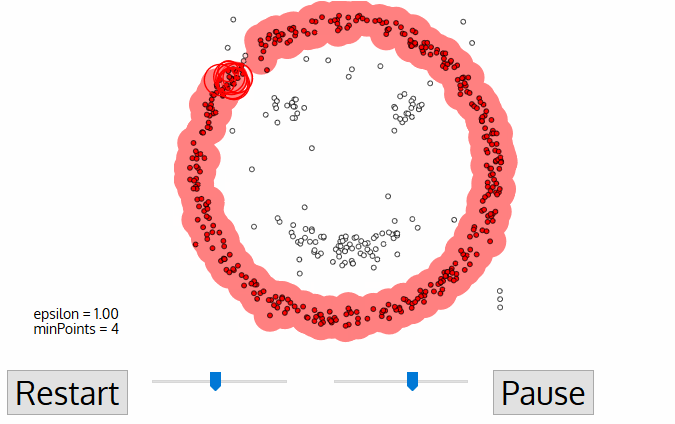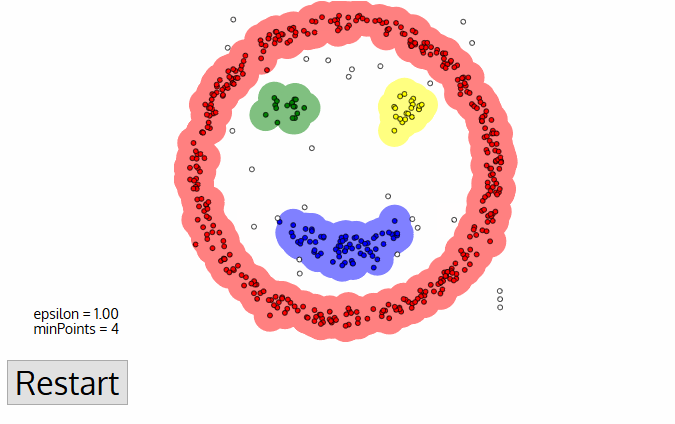
1. DBSCAN începe cu un arbitrar de pornire punct de date care nu a fost vizitat. Vecinătatea acestui punct este extrasă folosind o distanță Epsilon ε (toate punctele care se află în distanța ε sunt puncte de vecinătate).,
2. dacă există un număr suficient de puncte (în funcție de minPoints) în acest cartier, atunci procesul de grupare începe și punctul de date curent devine primul punct din noul cluster. În caz contrar, punctul va fi etichetat ca zgomot (mai târziu acest punct zgomotos ar putea deveni parte a clusterului). În ambele cazuri, acest punct este marcat ca „vizitat”.
3. pentru acest prim punct al noului cluster, punctele din vecinătatea distanței ε devin, de asemenea, parte a aceluiași cluster., Această procedură de a face ca toate punctele din vecinătatea ε să aparțină aceluiași cluster este apoi repetată pentru toate punctele noi care tocmai au fost adăugate grupului de cluster.
4. Acest proces de pașii 2 și 3 se repetă până când toate punctele din cluster sunt determinate nu.e toate punctele cadrul ε cartier de cluster au fost vizitate și etichetate.
5. odată ce am terminat cu cluster-ul curent, un nou punct nevizitat este preluat și procesat, ceea ce duce la descoperirea unui cluster sau a unui zgomot suplimentar. Acest proces se repetă până când toate punctele sunt marcate ca vizitate., Deoarece la sfârșitul acestui lucru toate punctele au fost vizitate, fiecare punct va fi marcat fie ca aparținând unui grup, fie ca fiind zgomot.

DBSCAN prezintă unele avantaje mari față de alți algoritmi de grupare. În primul rând, nu necesită deloc un număr pe-set de clustere. De asemenea, identifică valorile ca zgomote, spre deosebire de schimbarea medie, care le aruncă pur și simplu într-un cluster, chiar dacă punctul de date este foarte diferit. În plus, se pot găsi în mod arbitrar dimensiuni și în mod arbitrar în formă de clustere destul de bine.,principalul dezavantaj al DBSCAN este că nu funcționează la fel de bine ca alții atunci când grupurile sunt de densitate variabilă. Acest lucru este pentru setarea de la distanță prag ε și minPoints pentru identificarea cartier puncte va varia de la cluster la cluster, atunci când densitatea variază. Acest dezavantaj apare și în cazul datelor foarte dimensionale, deoarece din nou pragul de distanță ε devine dificil de estimat.,

așteptare–maximizare (EM) Clustering folosind modele de amestec Gaussian (GMM)

unul dintre dezavantajele majore ale K-mijloace este utilizarea naivă a valorii medii pentru Centrul de cluster. Putem vedea de ce acest lucru nu este cel mai bun mod de a face lucrurile uitându-ne la imaginea de mai jos. Pe partea stângă, se pare destul de evident pentru ochiul uman că există două clustere circulare cu rază diferită ‘ centrat la aceeași medie. K-Means nu se poate ocupa de acest lucru, deoarece valorile medii ale clusterelor sunt foarte apropiate., K-înseamnă, de asemenea, eșuează în cazurile în care clusterele nu sunt circulare, din nou, ca urmare a utilizării mediei ca centru de cluster.

Gaussian Mixture Models (Mmg) dă-ne mai multă flexibilitate decât K-means. Cu GMMs presupunem că punctele de date sunt distribuite Gaussian; aceasta este o presupunere mai puțin restrictivă decât a spune că sunt circulare prin utilizarea mediei., În acest fel, avem doi parametri pentru a descrie forma clusterelor: media și abaterea standard! Luând un exemplu în două dimensiuni, aceasta înseamnă că clusterele pot lua orice fel de formă eliptică (deoarece avem o abatere standard atât în direcțiile x, cât și în y). Astfel, fiecare distribuție Gaussiană este atribuită unui singur grup.

pentru a găsi parametrii Gaussian pentru fiecare cluster (de exemplu, media și deviația standard), Vom folosi un algoritm de optimizare numit Expectation–Maximization (EM)., Aruncati o privire la graficul de mai jos ca o ilustrare a Gaussians fiind montate la clustere. Apoi, putem continua cu procesul de așteptare–maximizarea clustering folosind GMM-uri.

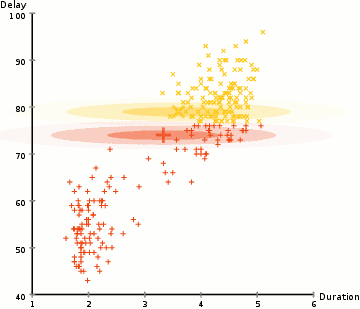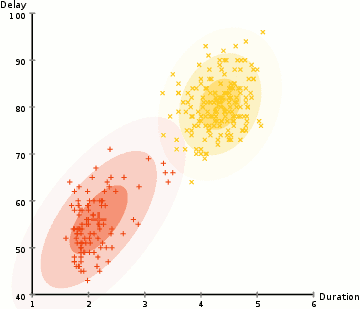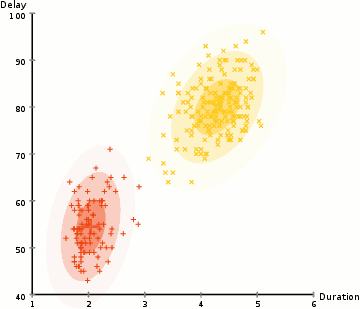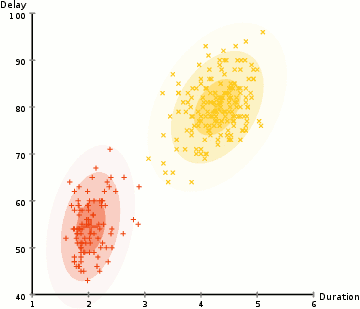
1. Vom începe prin selectarea numărului de clustere (cum ar fi K-means) și inițializează aleator cu distribuție Gaussiană parametri pentru fiecare cluster., Se poate încerca să ofere un guesstimate bun pentru parametrii inițiali de a lua o privire rapidă la datele prea. Deși rețineți, așa cum se poate vedea în graficul de mai sus, acest lucru nu este 100% necesar, deoarece Gaussienii încep să fie foarte săraci, dar sunt rapid optimizați.
2. având în vedere aceste distribuții gaussiene pentru fiecare cluster, calculați probabilitatea ca fiecare punct de date să aparțină unui anumit cluster. Cu cât un punct este mai aproape de centrul Gaussian, cu atât este mai probabil să aparțină acelui grup., Acest lucru ar trebui să aibă sens intuitiv, deoarece cu o distribuție Gaussiană presupunem că majoritatea datelor se află mai aproape de centrul clusterului.
3. Pe baza acestor probabilități, calculăm un nou set de parametri pentru distribuțiile gaussiene, astfel încât să maximizăm probabilitățile punctelor de date din clustere. Calculăm acești parametri noi folosind o sumă ponderată a pozițiilor punctelor de date, unde greutățile sunt probabilitățile punctului de date aparținând acelui cluster., Pentru a explica acest lucru vizual, putem arunca o privire la graficul de mai sus, în special clusterul galben ca exemplu. Distribuția începe aleatoriu la prima iterație, dar putem vedea că majoritatea punctelor galbene sunt la dreapta acelei distribuții. Când calculăm o sumă ponderată de probabilități, chiar dacă există unele puncte în apropierea centrului, cele mai multe dintre ele sunt pe dreapta. Astfel, în mod natural, media distribuției este deplasată mai aproape de acele puncte. De asemenea, putem vedea că majoritatea punctelor sunt „de sus-dreapta până la stânga jos”., Prin urmare, deviația standard se modifică pentru a crea o elipsă care este mai potrivită acestor puncte, pentru a maximiza suma ponderată de probabilități.
4. pașii 2 și 3 se repetă iterativ până la convergență, unde distribuțiile nu se schimbă prea mult de la iterație la iterație.

există 2 avantaje cheie pentru utilizarea MMG-urilor. În primul rând GMM-urile sunt mult mai flexibile în ceea ce privește covarianța clusterului decât K-înseamnă; datorită parametrului deviației standard, clusterele pot lua orice formă de elipsă, mai degrabă decât să fie limitate la cercuri., K-Means este de fapt un caz special de GMM în care covarianța fiecărui cluster de-a lungul tuturor dimensiunilor se apropie de 0. În al doilea rând, deoarece GMM-urile folosesc probabilități, ele pot avea mai multe clustere pe punct de date. Deci, dacă un punct de date se află în mijlocul a două clustere suprapuse, putem defini pur și simplu clasa sa spunând că aparține x-procente clasei 1 și Y-procente clasei 2. Adică GMM-urile sprijină apartenența mixtă.algoritmii de grupare ierarhică aglomerată se încadrează în 2 categorii: de sus în jos sau de jos în sus., Algoritmii de jos în sus tratează fiecare punct de date ca un singur cluster la început și apoi fuzionează succesiv (sau aglomerează) perechi de clustere până când toate clusterele au fost îmbinate într-un singur cluster care conține toate punctele de date. Gruparea ierarhică de jos în sus se numește, prin urmare, gruparea aglomerată ierarhică sau HAC. Această ierarhie a clusterelor este reprezentată ca un copac (sau dendrogram). Rădăcina arborelui este clusterul unic care adună toate probele, frunzele fiind clusterele cu un singur eșantion., Verificați graficul de mai jos pentru o ilustrare înainte de a trece la algoritmul de pași

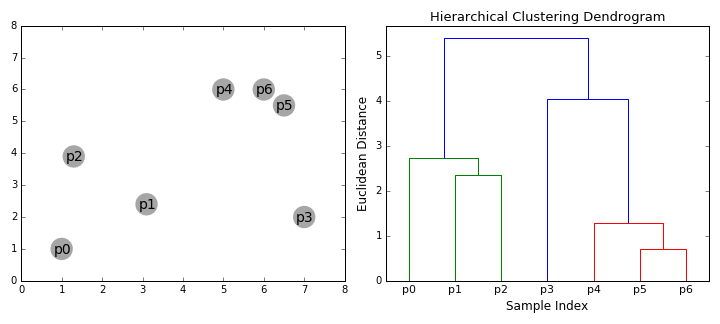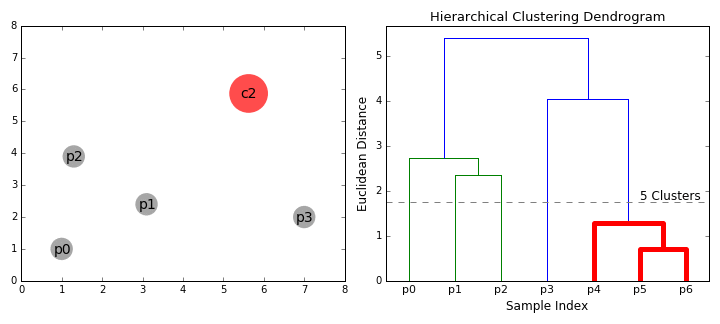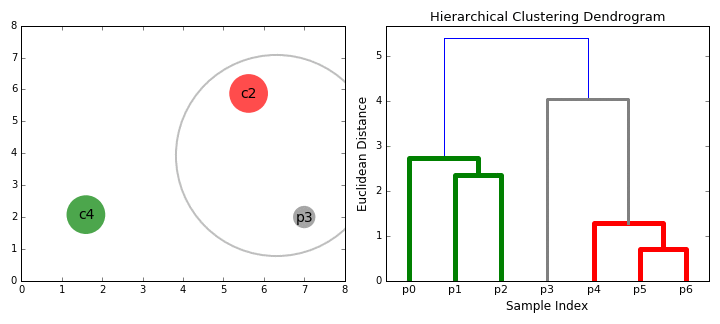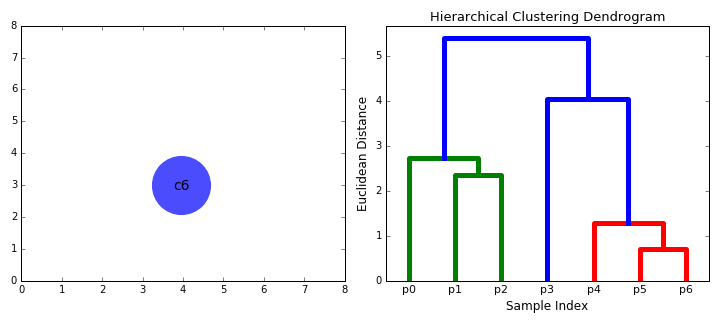
1. Vom începe prin a trata fiecare punct de date ca un singur cluster eu.e dacă există X puncte de date din setul nostru de date, atunci avem X clustere. Apoi selectăm o valoare de distanță care măsoară distanța dintre două clustere., De exemplu, vom folosi legătura medie care definește distanța dintre două clustere pentru a fi distanța medie dintre punctele de date din primul cluster și punctele de date din al doilea cluster.
2. pe fiecare iterație, combinăm două clustere într-una. Cele două clustere care urmează să fie combinate sunt selectate ca cele cu cea mai mică legătură medie. I. e potrivit selectate distanța metrică, aceste două grupuri au cea mai mică distanță între ele și, prin urmare, sunt cele mai similare și ar trebui să fie combinate.
3. Pasul 2 se repetă până când ajungem la rădăcina copacului i.,e avem doar un singur cluster care conține toate punctele de date. În acest fel, putem selecta câte clustere dorim în cele din urmă, pur și simplu alegând când să oprim combinarea clusterelor, adică atunci când oprim construirea copacului!gruparea ierarhică nu ne cere să specificăm numărul de clustere și putem chiar să selectăm ce număr de clustere arată cel mai bine, deoarece construim un arbore. În plus, algoritmul nu este sensibil la alegerea metricii distanței; toate acestea tind să funcționeze la fel de bine, în timp ce cu alți algoritmi de grupare, alegerea metricii distanței este critică., Un caz deosebit de bun de utilizare a metodelor de grupare ierarhică este atunci când datele de bază au o structură ierarhică și doriți să recuperați ierarhia; alți algoritmi de grupare nu pot face acest lucru. Aceste avantaje ale clustering ierarhice vin la costul de eficiență mai mică, deoarece are o complexitate de timp de O (n3), spre deosebire de complexitatea liniară A K-mijloace și GMM.