distribuții
problema de bază în centrul problemelor cu Delta Dirac și obiecte matematice similare
este problema diferențiabilității. După cum a afirmat Dirac în citatul de mai sus, nu vă confruntați cu probleme dacă folosiți funcția δ ca regulă simbolică pentru modul în care acționează asupra altor funcții; cu toate acestea, el continuă să diferențieze δ în calculele sale și de aici încep cu adevărat problemele., Cum se poate cunoaște a priori „când aceste operațiuni sunt permise” atunci când nu există nici măcar o definiție fermă a obiectelor sau ce ar însemna diferențierea acestora? Vom vedea cum aceste întrebări duc la derivarea unor obiecte matematice noi și riguros definite.
funcții
luați în considerare modul în care se determină în mod normal derivatul (sau antiderivativul) unei funcții. În condiții normale, cu funcții „clasice”, aveți o regulă bine definită care descrie modul în care o funcție mapează un set de numere reale la un alt set, spune f : ℝ →ℝ., Având în vedere acest lucru și definițiile integralei sau derivatului, se poate investiga în mod clar valorile pe care acești operatori le obțin atunci când sunt aplicate funcției. În cazul δ, nu avem o definiție funcțională pentru a continua de-a lungul acestor linii. În schimb, în practică δ este cel mai proeminent definit de modul în care funcționează pe alte funcții bine definite (ca în (3)). Aceasta este perspectiva cheie care duce la teoria modernă a distribuțiilor. Se pare că modul corect de a trata matematic δ și o clasă mare de obiecte similare este să nu mai încercați să le definiți ca funcții., Această linie de gândire este bine descrisă de Jean Dieudonne în cronica sa (a se vedea ):
… începe cu o familie de „regulat” funcții (de obicei cu
respect pentru diferențial proprietăți), care îndeplinesc anumite (în general
integral) relații, sau pe care anumite operațiuni sunt posibile; și
apoi descopera ca un apriori mai mare familie de funcții îndeplinește
aceleași relații, sau pot fi supuse unor operațiuni similare. Multe
întrebări atunci pot fi puse în mod natural: este această nouă familie într-adevăr
diferită de prima?, Dacă este, care sunt relațiile dintre cele două familii și se poate da o descriere precisă a celei noi?doar în ultima etapă a ” preistoriei „va apărea ceea ce poate fi numit punct de vedere revoluționar, cu ideea că” noua familie ” ar putea consta din alte obiecte decât funcții.
celelalte obiecte la care se face aluzie sunt funcționale. Vă puteți gândi la un
funcțional ca o funcție a funcțiilor., Deoarece o funcție este o mapare unică de la un set de numere
la altul, un F funcțional poate fi definit ca o mapare F: C →ℝ,
unde C este un set de funcții. Adică, o funcție funcțională hărți reale
Numere., Un exemplu simplu de o funcțională de acest tip este integralei definite:

care are în mod clar o funcție f de un set corespunzător de funcții integrabile și hărți pentru un număr real, valoarea integrală, sau aria de sub curba f(x) între a și b. Acesta este doar un singur exemplu., Se poate imagina un număr infinit de funcții și seturi de funcții; s-ar putea continua chiar generalizarea și definirea mapărilor de la seturi de funcții la numere reale. Asta nu e nici aici, nici acolo. Ceea ce este important este faptul că conceptul funcțional poate fi utilizat pentru a defini distribuții.
setul de funcții de testare
avem nevoie de încă o definiție pentru a ne atinge obiectivul. Aceasta înseamnă specificarea setului C de funcții din care distribuțiile vor cartografia funcțiile la numere reale., Funcțiile sunt adesea colectate în seturi care specifică gradul lor de continuitate, diferențiabilitate și continuitatea derivatelor lor. Spunem că o funcție f este în set C⁰ (scrie f ∈ C⁰) dacă este continuă pe întreaga linie reală, în sensul că limita de la toate punctele este aceeași atunci când luate la stânga sau la dreapta; nu este neapărat derivabile. Spunem că f ∈ C1 dacă derivatul său există și este continuu, adică f ‘ ∈ C⁰. De exemplu, funcția g(x) = |x| este continuă, dar nu derivabila in x= 0; g este în C⁰ dar nu în C1., Putem generaliza acest lucru și putem spune că Cⁿ este setul de funcții care au pentru funcțiile continue primele lor n derivate, unde n este un număr întreg.pe măsură ce n devine mai mare, seturile devin într-un sens „mai mici”; puteți găsi întotdeauna funcții (infinit de multe!) care sunt în Cⁿ, dar nu Cⁿ ⁺ 1. Aceste „spații de continuitate” formează, prin urmare, o secvență de subseturi imbricate, așa cum este descris mai jos.

în partea de jos a acestei secvență infinită de seturi de funcții găsim set
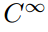
care este, desigur, un set de toate funcțiile care au infinit mai multe continuă derivate. Multe funcții bine cunoscute și prietenoase sunt în această din urmă clasă (de exemplu, sin(x); cos(x); eˣ; toate polinoamele)., Aceste funcții sunt numite „netede” sau „bine comportate”, deoarece se poate efectua operația de diferențiere asupra lor de câte ori se dorește fără grijă. Dar, în timp ce acest set are cu siguranță infinit de mulți membri, ele sunt rare în sensul că majoritatea funcțiilor nu sunt atât de bine comportate.
setul care este potrivit pentru definirea distribuțiilor este chiar mai mic decât acesta. Este nevoie de un criteriu suplimentar: că funcțiile au suport compact. Acest termen tehnic înseamnă pur și simplu că o funcție are valori zero într-un domeniu finit și este uniform zero în afara acestuia., Prin urmare, vom folosi notația
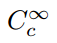
pentru a desemna un set de infinit continuu derivabile funcțiile programului compact, și apela aceste funcții funcții de test. Pentru a defini o clasă de funcții folosind acest set ca domeniu, ar trebui să fim siguri că există de fapt membri ai acestui set., One example is the so-called bump function,

Feel free to verify that the bump function is a test function via differentiation. In fact there are uncountably infinitely many test functions.

Definitie
Din acest punct definiția de distribuție este simplă. O distribuție este o funcțională liniară
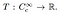
Care este, este o mapare de la un set de funcții de test de la un număr real. Analog cu modul în care o funcție specifică acționează asupra unui număr de intrare și produce o ieșire, distribuțiile specifice sunt definite de modul în care transformă funcțiile de testare în numere., Acțiunea de distribuție a funcției de testare φ poate fi scrisă ca T (φ), sau în mod obișnuit ca〈T, φ〉.
se poate vedea acum de ce distribuțiile sunt numite funcții generalizate. Pentru orice
clasic funcție pentru care integrala

este bine definit, există o distribuție corespunzătoare F astfel încât / b > F,φ〉dă valoarea acestei integrale., Cu toate acestea, există și distribuții care nu corespund funcțiilor clasice; distribuțiile sunt mai generale. După cum ar trebui să fie clar până acum, exemplul canonic al unei distribuții care nu corespunde unei funcții Clasice este Dirac δ., Prin urmare, în cele din urmă ajunge la un complet definirea riguroasa a δ ca distribuție, astfel încât

Generalizate sau „Slab” Derivat
δ distribuție este doar unul din infinit de multe distribuții care nu
corespund clasice funcții. Putem obține unele mai multe dintre acestea prin diferențierea δ în sensul distribuțiilor., Dar cum rezolvă conceptul de distribuție
problema diferențierii așa cum am discutat mai devreme? Trebuie doar să generalizăm conceptul de diferențiere pentru a se aplica distribuțiilor.
luați în considerare o funcție f ∈ C1, astfel încât să fie diferențiată în mod continuu. Calculeaza folosind integrarea prin părți, vom vedea că

Termenul în paranteze dispare deoarece φ, ca o funcție de test, a programului compact., Acest generalizează la o distribuție, spune F’, corespunzătoare funcției f’:

Acest calcul generalizează destul de ușor să distribuții care nu corespund clasică a funcției f., În acest fel, putem defini derivata T’ T în sens de distribuții:

Acest lucru este, de asemenea, uneori menționată ca slab derivat, deoarece se extinde instrumente financiare derivate pentru funcții care în mod normal nu ar fi derivabila. Aceasta generalizează și mai mult, la derivatele de ordin superior., Putem defini cel mai inalt derivat de o distribuție T ca T⁽ⁿ⁾, în cazul în care acesta din urmă este cel de distribuție, astfel încât

Aici,
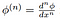
este clasică derivat de funcția de test, care este asigurat
de a exista prin definiția de funcții de test!, Rezultă că toate distribuțiile sunt infinit diferențiabile (în sensul distribuțiilor).aceasta elimină în întregime lupta cu care Dirac și alții s-au confruntat atunci când au diferențiat funcția δ. Prin ceea ce am definit aici, un derivat al δ pur și simplu cerne pentru valoarea unui alt derivat de funcții la zero., În mod oficial,

Acest lucru oferă un matematice riguroase cadru pentru derivații de δ, care a apărut în literatura de specialitate cu mult înainte de această teorie a venit în existență.există o serie de alte operații care se aplică funcțiilor care au fost generalizate pentru a se aplica distribuțiilor. Acestea pot fi adăugate și scăzute, convoluate și transformate folosind transformatele Laplace și Fourier., Cu toate acestea, este imposibil să se definească multiplicarea distribuțiilor într-un mod care să păstreze algebra care se aplică funcțiilor clasice (Teorema imposibilității Schwartz).