
Leonardo din Pisa (Fibonacci) (c.1170-1250)
Cel de-al 13-Lea Italian Leonardo din Pisa, cunoscut după porecla lui Fibonacci, a fost probabil cel mai talentat matematician al occidentului din Evul mediu. Se știe puțin despre viața sa, cu excepția faptului că a fost fiul unui oficial vamal și, în copilărie, a călătorit în Africa de Nord cu tatăl său, unde a învățat despre matematica Arabă., La întoarcerea sa în Italia, el a ajutat la diseminarea acestor cunoștințe în întreaga Europă, punând astfel în mișcare o întinerire a matematicii Europene, care a rămas în mare parte latentă timp de secole în timpul Evului întunecat.
în special, în 1202, el a scris o carte extrem de influentă numită „Liber Abaci” („cartea de calcul”), în care a promovat utilizarea sistemului numeric hindus-arab, descriind numeroasele sale beneficii pentru comercianți și matematicieni deopotrivă asupra sistemului stângace de cifre romane utilizate atunci în Europa., În ciuda avantajelor sale evidente, absorbția de sistem în Europa a fost lent (aceasta a fost, după toate în timpul Cruciadelor împotriva Islamului, un timp în care nimic arabă a fost privit cu mare suspiciune), și cu cifre arabe au fost chiar interzise în orașul Florența, în 1299, sub pretextul că au fost mai ușor de falsificat decât cifre Romane. Cu toate acestea, bunul simț a predominat în cele din urmă și Noul sistem a fost adoptat în întreaga Europă până în secolul al XV-lea, făcând sistemul Roman învechit., Notația barei orizontale pentru fracții a fost, de asemenea, folosită pentru prima dată în această lucrare (deși urmând practica arabă de plasare a fracției la stânga numărului întreg).Fibonacci este cel mai bine cunoscut pentru introducerea sa în Europa a unei anumite secvențe de numere, care de atunci a devenit cunoscută sub numele de numere Fibonacci sau secvența Fibonacci., El a descoperit secvența – prima secvență de numere recursive cunoscută în Europa – luând în considerare o problemă practică în „Liber Abaci” care implică creșterea unei populații ipotetice de iepuri bazată pe ipoteze idealizate. El a menționat că, după fiecare lunare generație, numărul de perechi de iepuri au crescut de la 1 la 2 la 3 la 5 la 8 la 13, etc, și cum identificate secvența progresat prin adăugarea de ultimii doi termeni (în termeni matematici, Fn = Fn-1 + Fn-2), o secvență care ar putea, în teorie prelungi pe termen nedefinit.,
secvență, care a fost de fapt cunoscut la Indian matematicieni din secolul al 6-Lea, are multe proprietăți matematice, și multe dintre implicațiile și relațiile de succesiune nu s-au descoperit până la câteva secole după moartea lui Fibonacci., De exemplu, secvența se regenerează în unele moduri surprinzătoare: fiecare al treilea număr F este divizibil cu 2 (F3 = 2), fiecare al patrulea număr F este divizibil cu 3 (F4 = 3), fiecare a cincea F-numărul este divizibil cu 5 (F5 = 5), fiecare al șaselea număr F este divizibil prin 8 (F6 = 8), fiecare al șaptelea număr F este divizibil cu 13 (F7 = 13), etc., Numerele de secvență a fost, de asemenea, găsite de a fi omniprezent în natură: printre alte lucruri, multe specii de plante cu flori au numere de petale în Secvența Fibonacci; spirala aranjamente de ananas apar în 5s și 8s, cei de conuri de pin in 8s și 13s, și semințe de floarea-soarelui capul în 21, 34, 55 de ani sau chiar mai mare de termeni din șir; etc.,
Raportul De Aur φ
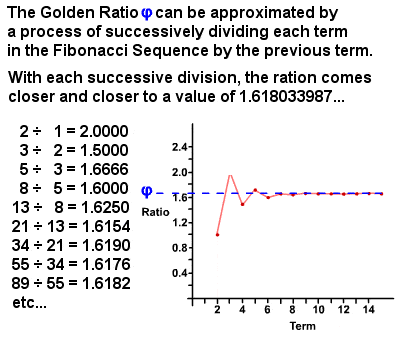
Raportul De Aur φ pot fi derivate din șirul lui Fibonacci
În 1750, Robert Simson remarcat faptul că raportul dintre fiecare termen din șirul lui Fibonacci și termenul anterior se apropie, cu o mai mare acuratețe mai mare de termeni, un raport de aproximativ 1 : 1.6180339887 (este de fapt un număr irațional egal cu (1 + √5)⁄2 care a fost calculată la mii de zecimale)., Această valoare este denumită raportul de aur, cunoscut și sub numele de media de aur, secțiunea de aur, proporția divină etc. și este de obicei notată cu litera greacă phi φ (Sau uneori litera majusculă Phi Φ). În esență, două cantități sunt în raportul de aur dacă raportul dintre suma cantităților și cantitatea mai mare este egal cu raportul dintre cantitatea mai mare și cea mai mică. Raportul de Aur în sine are multe proprietăți unice, cum ar fi 1⁄φ = φ – 1 (0.618…) și φ2 = φ + 1 (2.618…), și există nenumărate exemple de acesta pentru a fi găsite atât în natură și în lumea umană.,
Un dreptunghi cu laturile în raport de 1 : φ este cunoscut ca un Dreptunghi de Aur, și mulți artiști și arhitecți de-a lungul istoriei (datând înapoi la Egiptul antic și Grecia, dar deosebit de popular în arta Renascentistă a lui Leonardo da Vinci și contemporanii săi) au proportionat lor funcționează aproximativ utilizând Raportul de Aur și de Aur Dreptunghiuri, care sunt considerate a fi innascuta punct de vedere estetic. Un arc care leagă punctele opuse ale dreptunghiurilor de aur imbricate tot mai mici formează o spirală logaritmică, cunoscută sub numele de spirală de aur., Raportul de aur și spirala de aur pot fi găsite, de asemenea, într-un număr surprinzător de cazuri în natură, de la scoici la flori la coarne de animale la corpuri umane la sisteme de furtună pentru a completa galaxiile.,
ar trebui să fie amintit, totuși, că lui Fibonacci a fost de fapt doar un element minor în „Liber Abaci” – într-adevăr, secvența a primit doar Fibonacci numele în 1877 când Eduouard Lucas a decis să plătească tribut pentru el numindu-seria după el – și că Fibonacci însuși nu a fost responsabili pentru identificarea oricăror dintre cele mai interesante proprietăți matematice ale secvenței, relația sa cu Aur și Aur Dreptunghiuri și Spirale, etc.,
Lattice Multiplicare
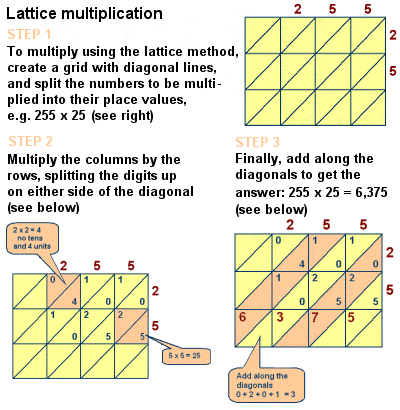
Fibonacci introdus lattice multiplicare în Europa
cu toate Acestea, influența cărții asupra medieval matematică este de netăgăduit, și include, de asemenea, discuții de o serie de alte probleme matematice, cum ar fi Chinezii Teorema Rest, perfect de numere și numere prime, formule pentru serii aritmetice și pentru piața piramidal numere, geometrie Euclidiană, și un studiu de ecuații liniare simultane de-a lungul liniilor de Diophantus și Al-Karaji., El a descris, de asemenea, metoda de multiplicare cu zăbrele (sau sită) a înmulțirii numerelor mari, o metodă – inițial pionieră de matematicieni islamici precum Al-Khwarizmi – echivalentă algoritmic cu înmulțirea lungă.
nici „Liber Abaci” nu a fost singura carte a lui Fibonacci, deși a fost cea mai importantă., Lui „Liber Quadratorum” („Cartea de Pătrate”), de exemplu, este o carte pe algebra, publicat în 1225, în care apare o declarație a ceea ce este numit acum Fibonacci de identitate – uneori, de asemenea, cunoscut sub numele de Brahmagupta identitatea după mult mai devreme Indian matematician care, de asemenea, a ajuns la aceeași concluzie – că produsul a două sume de două pătrate este în sine o sumă de două pătrate de exemplu (12 + 42)(22 + 72) = 262 + 152 = 302 + 12.,
| << Back to Medieval Mathematics | Forward to 16th Century Mathematics >> |