Învățării
- să se familiarizeze cu istoria de pozițional numărul de sisteme
- Identifica bazele care au fost utilizate în numărul de sisteme din punct de vedere istoric
- a Converti numere între bazele
- Utilizarea a două metode diferite de conversie a numerelor între bazele
Spate
Ca s-ar putea imagina, dezvoltarea unui sistem de bază este un pas important în a face procesul de numărare mai eficient., Sistemul nostru de bază-ten a apărut probabil din faptul că avem 10 degete (inclusiv degetele mari) pe două mâini. Aceasta este o dezvoltare naturală. Cu toate acestea, alte civilizații au avut o varietate de baze, altele decât zece. De exemplu, nativii din Queensland au folosit un sistem de bază-două, numărând după cum urmează: „unu, doi, doi și unu, doi doi, mult.”Unele triburi moderne din America de Sud au un sistem de bază-cinci care numără în acest fel:” unu, doi, trei, patru, mână, mână și una, mână și două ” și așa mai departe. Babilonienii au folosit un sistem de bază-șaizeci (sexigesimal)., În acest capitol, încheiem cu un exemplu specific de civilizație care a folosit de fapt un alt sistem de bază decât 10.
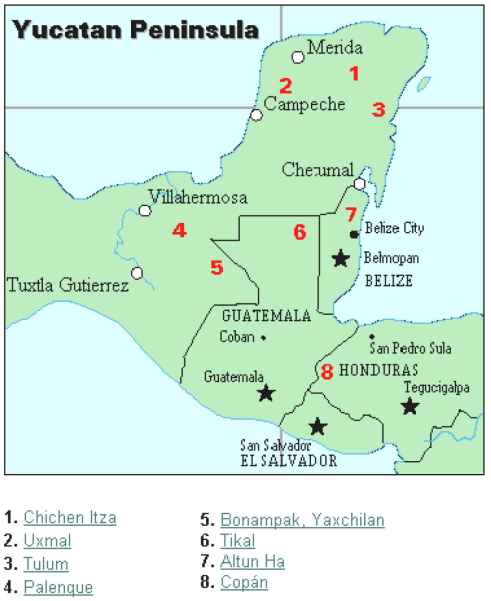 civilizația Maya este în general datată din 1500 î.HR. până în 1700 CE. Peninsula Yucatan (vezi figura 16) din Mexic a fost scena dezvoltării uneia dintre cele mai avansate civilizații ale lumii antice. Mayașii aveau un sistem ritual sofisticat, care era supravegheat de o clasă preoțească. Această clasă de preoți a dezvoltat o filozofie cu timpul ca divină și eternă., Calendarul și calculele legate de acesta au fost astfel foarte importante pentru viața rituală a clasei preoțești și, prin urmare, pentru poporul Maya. De fapt, o mare parte din ceea ce știm despre această cultură provine din înregistrările lor calendaristice și din datele astronomice. O altă sursă importantă de informații despre mayași sunt scrierile părintelui Diego de Landa, care a plecat în Mexic ca misionar în 1549.
civilizația Maya este în general datată din 1500 î.HR. până în 1700 CE. Peninsula Yucatan (vezi figura 16) din Mexic a fost scena dezvoltării uneia dintre cele mai avansate civilizații ale lumii antice. Mayașii aveau un sistem ritual sofisticat, care era supravegheat de o clasă preoțească. Această clasă de preoți a dezvoltat o filozofie cu timpul ca divină și eternă., Calendarul și calculele legate de acesta au fost astfel foarte importante pentru viața rituală a clasei preoțești și, prin urmare, pentru poporul Maya. De fapt, o mare parte din ceea ce știm despre această cultură provine din înregistrările lor calendaristice și din datele astronomice. O altă sursă importantă de informații despre mayași sunt scrierile părintelui Diego de Landa, care a plecat în Mexic ca misionar în 1549.
 au existat două sisteme numerice dezvoltate de mayași—unul pentru oamenii obișnuiți și unul pentru preoți., Nu numai că aceste două sisteme au folosit simboluri diferite, dar au folosit și sisteme de bază diferite. Pentru preoți, sistemul de numere era guvernat de ritual. Zilele anului au fost considerate a fi zei, astfel încât simbolurile formale pentru zile au fost decorate capete, cum ar fi eșantionul din stânga deoarece calendarul de bază a fost bazat pe 360 de zile, sistemul numeric preoțesc a folosit un sistem de bază mixt care utilizează multipli de 20 și 360. Acest lucru face ca un sistem confuz, detaliile pe care le vom sări peste.,/td>
au existat două sisteme numerice dezvoltate de mayași—unul pentru oamenii obișnuiți și unul pentru preoți., Nu numai că aceste două sisteme au folosit simboluri diferite, dar au folosit și sisteme de bază diferite. Pentru preoți, sistemul de numere era guvernat de ritual. Zilele anului au fost considerate a fi zei, astfel încât simbolurile formale pentru zile au fost decorate capete, cum ar fi eșantionul din stânga deoarece calendarul de bază a fost bazat pe 360 de zile, sistemul numeric preoțesc a folosit un sistem de bază mixt care utilizează multipli de 20 și 360. Acest lucru face ca un sistem confuz, detaliile pe care le vom sări peste.,/td>
The Mayan Number System
Instead, we will focus on the numeration system of the „common” people, which used a more consistent base system., Așa cum am spus mai devreme, mayașii au folosit un sistem base-20, numit sistemul „vigesimal”. Ca și sistemul nostru, este pozițional, ceea ce înseamnă că poziția unui simbol numeric indică valoarea locului său. În tabelul următor puteți vedea valoarea locului în formatul său vertical.
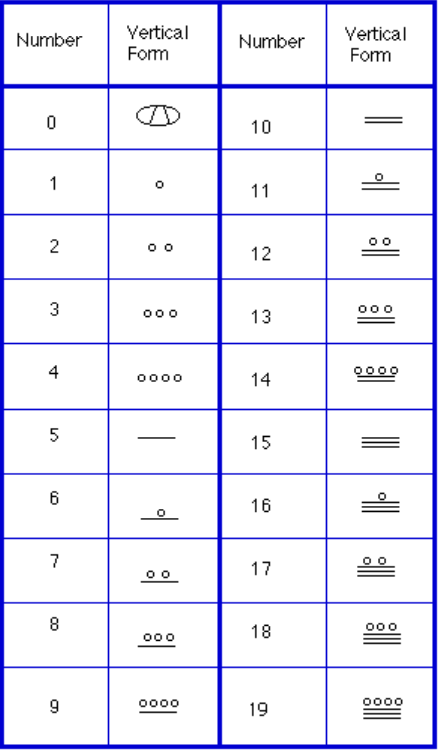
pentru a scrie numerele, au fost necesare doar trei simboluri în acest sistem. O bară orizontală a reprezentat cantitatea 5, un punct a reprezentat Cantitatea 1, iar un simbol special (considerat a fi o coajă) a reprezentat zero., Este posibil ca sistemul Maya să fi fost primul care a folosit zero ca înlocuitor/număr. Primele 20 de numere sunt afișate în tabelul din dreapta.
spre deosebire de sistemul nostru, unde locul începe din dreapta și apoi se mișcă spre stânga, sistemele Maya le plasează pe cele din partea de jos a unei orientări verticale și se deplasează în sus pe măsură ce valoarea locului crește.când numerele sunt scrise în formă verticală, nu trebuie să existe niciodată mai mult de patru puncte într-un singur loc. Când scrieți numere Maya, fiecare grup de cinci puncte devine o bară., De asemenea, nu ar trebui să existe niciodată mai mult de trei bare într-un singur loc…patru bare ar fi convertite într-un punct în următorul loc în sus. Este la fel ca 10 obtinerea convertit la un 1 în locul următor până când vom transporta în timpul adăugării.
exemplu
care este valoarea acestui număr, care este prezentată în formă verticală?
Exemplu
Ce este valoarea de următoarele numărul Maya?,
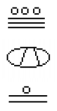
încercați
convertiți numărul Maya de mai jos în baza 10.,

Exemplu
Conversie în baza 10 numărul 357510 să Maya cifre.
scrierea numerelor cu baze mai mari de 10
când baza unui număr este mai mare de 10, separați fiecare „cifră” cu o virgulă pentru a face separarea cifrelor clară.
de exemplu, în baza 20, pentru a scrie numărul corespunzător 17 × 202 + 6 × 201 + 13 × 200, am scrie 17,6,1320.
în următorul videoclip vă prezentăm mai multe exemple despre cum să scrieți numere folosind cifre Maya, precum și conversia cifrelor scrise în Maya pentru în formularul de bază 10.,următorul videoclip prezintă mai multe exemple de conversie a numerelor de bază 10 în cifre Maya.
adăugarea numerelor Maya
când adăugăm numere Maya împreună, vom adopta o schemă pe care mayașii probabil că nu au folosit-o, dar care ne va face viața mai ușoară.
Exemplu
se Adaugă, în Maya, numerele 37 și 29:

încercați să-l
încercați să adăugați 174 și 78 în Maya de conversie mai întâi la numere Maya și apoi de lucru în întregime în acel sistem. Nu adăugați în bază-zece (zecimal) până la sfârșit când vă verificați munca.
în ultimul videoclip vom arăta mai multe exemple de adăugare a cifrelor Maya.,în acest modul, am schițat pe scurt dezvoltarea numerelor și a sistemului nostru de numărare, cu accent pe partea „scurtă”. Există numeroase surse de informații și de cercetare care umplu multe volume de cărți pe această temă. Din păcate, nu putem începe să ne apropiem de acoperirea tuturor informațiilor care există.

Am zgâriat doar suprafața de avere de cercetare și informații care există pe dezvoltarea de numere și numărare a lungul istoriei umane., Ceea ce este important de menționat este că sistemul pe care îl folosim în fiecare zi este un produs de mii de ani de progres și dezvoltare. Reprezintă contribuțiile multor civilizații și culturi. Nu vine la noi din cer, un dar de la zei. Nu este crearea unui editor de manuale. Este într-adevăr la fel de uman ca și noi, la fel ca și restul matematicii. În spatele fiecărui simbol, formulă și regulă există o față umană care trebuie găsită sau cel puțin căutată.mai mult, sperăm că acum aveți o apreciere de bază pentru cât de interesante și diverse sisteme de numere pot obține., De asemenea, suntem destul de siguri că ați început, de asemenea, să recunoașteți că luăm propriul nostru sistem de numere de la sine atât de mult încât atunci când încercăm să ne adaptăm la alte sisteme sau baze, ne aflăm cu adevărat nevoiți să ne concentrăm și să ne gândim la ceea ce se întâmplă.







